初一数学单元测验试题二
一、填空题
 1、多项式21x2y6z+14x4y3各项的公因式是
。
1、多项式21x2y6z+14x4y3各项的公因式是
。
2、25a2+mab+4b2是完全平方式,则m= 。
3、X2+3X+K是完全平方式,则K= 。
4、如图∵∠CED=∠ (已知)
∴AC∥DF( )
5、如图∵AB∥CD(已知)
∴∠EDF=∠ ( )
6、命题“等角的补角相等”的题设是 结论是 .
7、计算472+2×47×43+432= ; 2.332×4-2.222×9= 。
8、若x-y=5,xy=6,则xy2-x2y= ,(x+y)2= 。
9、某人从点A向北偏东72°方向走到点B,再自点B向北偏西58°方向走到C,则∠ABC= °。
10、已知a=9988,b=25,则![]() =
。
=
。
二、选择题
11、下列各式从左到向的变形是因式分解的是( )
A、(x-2)2=x2-4x+4 B、x2-4-3x=(x+2)(x-2)-3x
C、2x2-6x=2x2(1-![]() )
D、x2-y2+x-y=(x-y)(x+y+1)
)
D、x2-y2+x-y=(x-y)(x+y+1)
12、如果a//b,b//c,那么a//c的依据是( )
A、平行公理 B、等量代换
C、平行于同一条直线的两直线平行
D、同旁内角互补,两直线平行
13、平面内三条直线的交点个数可能有( )
A、1个或3个 B、2个或3个
C、1个或2个或3个 D、0个或1个或2个或3个
14、“经过一点,有且只有一条直线与这条直线平行”是( )
A、定义 B、假命题
C、公理 D、定理
15、如果两条平行线被第三条直线所截,那么一组同位角的平分线的位置关系是( )
A、互相垂直
B、互相平行
C、相交但不垂直
D、不能确定
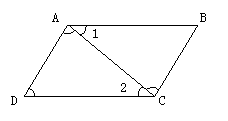 16、图中与∠1成内错角的个数是( )
16、图中与∠1成内错角的个数是( )
A、2个
B、3个
C、4个
D、5个
17、如图,已知∠1=∠2,∠BAD=∠BCD,则下列结论
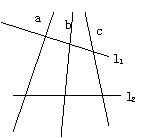 (1)AB//CD;(2)AD//BC;(3)∠B=∠D;(4)∠D=∠ACB。
(1)AB//CD;(2)AD//BC;(3)∠B=∠D;(4)∠D=∠ACB。
其中正确的有( )
A、1个 B、2个 C、3个 D、4个
18、下列命题中,假命题的个数是( )
(1)同位角相等;(2)若∠1+∠2=180°,则∠1与∠2是邻补角;(3)互余的两个角都小于45;(4)不相交的两条直线是平行线。
A、4个 B、3个 C、2个 D、1个
三、分解因式:
19、-6a2b2+15a2b3;
20、12x3-![]()
21、m2(a-m)(a-n)+n2(m-a)(a-n) 22、9(2a+b)2-25(a-b)2
23、![]() 24、(3x-1)3-(12x-4)
24、(3x-1)3-(12x-4)
25、x2-x-3y-9y2 26、4a2b2-9b2+8a2-18
27、(x3-4x2y+4xy2)-x+2y 28、4m2-n2-4m+1
29、(m2+2mn)2-(2mn+4n2)2 30、(x2-y2-1)2-4y2
四、填写理由
 31、已知:如图BE//CF,BE、CF分别平分∠ABC和∠BCD
31、已知:如图BE//CF,BE、CF分别平分∠ABC和∠BCD
求证:AB//CD
证明:∵BE、CF分别平分∠ABC和∠BCD(已知)
∴∠1=![]() ∠ ∠2=
∠ ∠2=![]() ∠
( )
∠
( )
∵BE//CF(已知)
∴∠1=∠2( )
∴![]() ∠ABC=
∠ABC=![]() ∠BCD(
)
∠BCD(
)
即∠ABC=∠BCD
∴AB//CD( )
 32、如图,已知:∠BCF=∠B+∠F。
32、如图,已知:∠BCF=∠B+∠F。
求证:经过点C画CD//AB
∴∠BCD=∠B。( )
∵∠BCF=∠B+∠F,(已知)
∴∠CDF=∠F。( )
∴CD//EF。( )
∴AB//EF( )
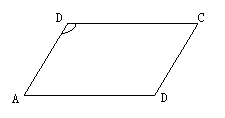 五、几何证明及计算
五、几何证明及计算
33、如图,已知:AB//CD,AD//BC
求证:∠B=∠D。
 |
34、已知:BC//EF,∠B=∠E,
求证:AB//DE。
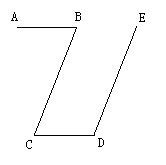 35、已知:如图,AB//CD,BC//DE,∠B=70°,求∠D的度数。
35、已知:如图,AB//CD,BC//DE,∠B=70°,求∠D的度数。
36、如图,已知DE//BC,BE平分∠ABC,∠C=55°,∠ABC=70°,求∠BED与∠BEC的度数。
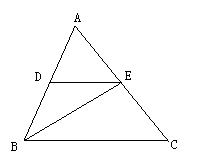 |
六、找规律,并解答下列问题。
37、已知 12+22+12×22=9=32
22+32+22×32=49=72
32+42+32×42=169=132
42+55+42×52=441=212
52+62+52×62=961=312
1002+101+1002×1012= 2。
一般地,有 ,并证明你的结论。
【答案】
一、填空题
1、7x2y3 2、±20 3、2.25
4、EDF 内错角相等,两直线平行
5、BFD 两直线平行,内错角相等
6、两个角是等角的补角 它们相等
7、8100 -22.64
8、-30
49 9、50 10、![]()
二、选择题
11、D 12、C 13、D 14、B 15、B 16、A 17、C 18、A
三、分解因式
19、解:原式=3a2b2(5b-2)
20、解:原式=![]()
21、解:原式=m2(a-m)(a-n)-n2(a-m)(a-n)=(a-m)(a-n)(m2-n2)=(a-m)(a-n)(m+n)(m-n)
22、解:原式=[3(2a+b)+5(a-b)][3(2a+b)-5(a-b)]=(a+8b)(11a-2b)
23、解:原式=-3xn-1(x2-2xy+y2)=-3xn-1(x-y)2
24、解:原式=(3x-1)3-4(3x-1)=(3x-1)[(3x-1)2-4]=(3x-1)(3x-3)=3(3x-1)(3x+1)(x-1)
25、解:原式=(3x+3y)(x-3y)-(x+3y)=(x+3y)(x-3y-1)
26、解:原式=b2(4a2-9)+2(4a2-9)=(b2+2)(2a+3)(2a-3)
27、解:原式=(x+3y)(x-3y)-(x+3y)=(x+3y)(x-3y-1)
28、解:原式=(2m-1)2-n2=(2m-1+n)(2m-1-n)
29、解:原式=(m2+2mn+2mn+4n2)(m2+2mn-2mn-4n2)
=(m+2n)2(m+2n)(m-2n)=(m+2n)3(m-2n)
30、解:原式=(x2-y2-1+2y)(x2-y2-1-2y)=(y2+1-2y-x2)(y2+1-2y-x2)
=(y-1-2y-x2)(y2+1+2y-x2)=(y-1+x)(y-1-x)(y+1+x)(y+1-x)
四、填写理由
31、 证明:∵BE、CF分别平分∠ABC和∠BCD(已知)
∴∠1=![]() ∠ ABC ∠2=
∠ ABC ∠2=![]() ∠ BCD (角平分线定义)
∠ BCD (角平分线定义)
∵BE//CF(已知)
∴∠1=∠2(两直线平行,内错角相等)
∴![]() ∠ABC=
∠ABC=![]() ∠BCD(等量代换)
∠BCD(等量代换)
即∠ABC=∠BCD
∴AB//CD(内错角相等,两直线平行)
32、如图,已知:∠BCF=∠B+∠F。
求证:经过点C画CD//AB
∴∠BCD=∠B。(两直线平行,内错角相等)
∵∠BCF=∠B+∠F,(已知)
∴∠CDF=∠F。(等式性质)
∴CD//EF。(内错角相等,两直线平行)
∴AB//EF(平行于同一直线的两直线平行)
五、几何证明及计算
33、证明:∵AB//CD(已知),
∴∠B+∠C=180°(两直线平行,同旁内角互补)
∵AD//BC(已知)
∴∠D+∠C=180°(两直线平行,同旁内角互补)
∴∠B=∠D(同角的补角相等)
34、证明:∵BC//EF(已知)
∴∠E=∠1(两直线平行,同位角相等)
∵∠B=∠E(已知)
∴∠B=∠1(等量代换)
∴AB//DE(同位角相等,两直线平行)
35、解:∵AB//CD(已知)
∴∠B=∠C(两直线平行,同旁内角互补)
∵BC//DE(已知)
∴∠C+∠D=180°(两直线平行,同旁内角互补)
∴∠B+∠D=180°(等量代换)
∵∠B=70° ∴∠D=180°-70°==110°(等式性质)
答:∠D为110°。
36、解:∵∠ABC=70°(已知)
BE平分∠ABC
∴∠1=![]() ∠ABC(角平分线定义)
∠ABC(角平分线定义)
∴∠1=70°![]() =35°
=35°
∵BE//BC(已知)
∴∠BED=∠1(两直线平行,内错角相等)
∴∠BED=35°
∵DE//BC(已知)
∴∠C+∠DEC=180°(两直线平行,同旁内角互补)
∴∠DEC=180°-55°=125°(等式性质)
∵∠BED+∠BEC=∠DEC
∴∠DCE=125° ∠BED=35°(已证)
∴∠BEC=90°(等式性质)
答:∠BED=35° ∠BEC=90°
六、a2+(a+1)2+a2×(a+1)2=[a2+(a+1)]2
证明:对“a2+(a+1)2+a2×(a+1)”进行因式分解
原式=(a2+a2+2a+1)+[a(a+1)]2
=2a(a+1)+1+[a(a+1)]2
=[a(a+1)+1]2=[a2+(a+1)]2
由此成见,推论结果成立。