初一数学期终几何复习
一、填空
![]() 1.如图6,已知CB=4,DB=7,D是AC的中点,
1.如图6,已知CB=4,DB=7,D是AC的中点,
则AC=_________ . <图6>
2.一个角的补角比它的余角大_____,若一个角的补角是它的余角的3倍,则这个角是_____
度.
3.时钟的时针和分针在2时20分时,所成的角度是_____度.
4.45°52′48″=_________度,126.31°=____°____′____″.
5.180°-56°42′32″=_____________,25°54′÷3=__________.
6.如图7,CB⊥AB,∠CBA与∠CBD的度数比是5:1,则∠DBA=________度,∠CBD
的补角是_________度.
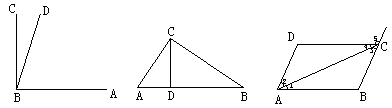 |
<图7> <图8> <图9>
7.如图8,AC⊥BC,CD⊥AB,点A到BC边的距离是线段_____的长,点B到CD边的
距离是线段_____的长,图中的直角有_____________,∠A的余角有_______________,
和∠A相等的角有__________.
8.如图9,当∠1=∠_____时,AB∥CD;当∠D+∠_____=180°时,AB∥CD;当∠B
=∠_____时,AB∥CD.
9.若两个角的两边分别平行,而一个角比另一个角的3倍少30°,则两个角的度数分别
是____________________.
10.命题“同角的余角相等”改写成“如果……, 那么……”的形式可写成
______________________________.
二、选择题
11.下列结论中错误的是( )
A.一个角的余角一定比它的补角小 B.凡直角都相等
C.定理是真命题 D.在直线、射线和线段中,直线最长
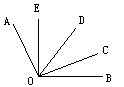 12.如图10,∠AOE=∠BOC,OD平分∠COE,
12.如图10,∠AOE=∠BOC,OD平分∠COE,
那么图中除∠AOE=∠BOC外,相等的角共
有( )
A.1对 B.2对
C.3对 D.4对 <图10>
13.互为余角的两个角之差为35°,则较大角的补角是( )
A.117.5° B.112.5° C.125° D.127.5°
 14.如图11,P为直线l外一点,A、B、C在l上,且PB⊥l,下列说法中,正确的个数
14.如图11,P为直线l外一点,A、B、C在l上,且PB⊥l,下列说法中,正确的个数
是( )
①PA、PB、PC三条线段中,PB最短
②线段PB的长叫做点P到直线l的距离
③线段AB的长是点A到PB的距离
④线段AC的长是点A到PC的距离 <图11>
A.1个 B.2个 C.3个 D.4个
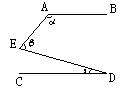
15.已知,如图12,AB∥CD,则∠α、∠β、∠γ之间的关系为( )
A.∠α+∠β+∠γ=360°
B.∠α-∠β+∠γ=180°
C.∠α+∠β-∠γ=180°
D.∠α+∠β+∠γ=180°
 | |||
 | |||
<图12> <图13>
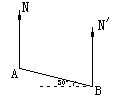
16.如图13,由A到B的方向是( )
A.南偏东30°
B.南偏东60°
C.北偏西30°
D.北偏西60°
17.下列三个命题
①同位角相等;②如果一个角的两边分别平行于另一个角的两边,则两个角一定相等;③两点之间的线段就是这两点间的距离.
其中正确的有( )
A.0个 B.1个 C.2个 D.3个
三、18.根据命题“角平分线上的点到角的两边距离相等”,画出图形,并结合图形写出
已知、求证.
四、解答题
19.如图14,M是AB的中点,AB=![]() BC,N是BD的中点,且BC=2CD,如果AB=2cm,
BC,N是BD的中点,且BC=2CD,如果AB=2cm,
求AD、AN的长.
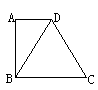 | 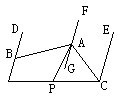 | ||||
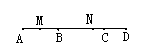 | |||||
<图14> <图15> <图16>
20.已知,如图15,AD∥BC,DA⊥AB,DB平分∠ADC,∠ABD=30°,求∠C的度数.
21.已知,如图16,DB∥FG∥EC,∠ABD=60°,∠ACE=36°,AP平分∠BAC,求
∠PAG的度数.
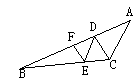
22.已知,如图17,AD平分∠BAC,点F在BD上,FE∥AD交AB于G,交CA的延
长线于E,求证:∠AGE=∠E.
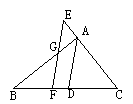
23.已知,如图18,CD平分∠ACB,DE∥AC,EF∥CD,求证:EF平分∠BED.
 | |||
 | |||
答案与提示
一、1.6 2.90,45 3.50 4.45.88;126;18;36
5.123°17′28″;8°38′ 6.72;162 7.AC;BD;∠ACB、∠ADC、
∠BDC;∠B、∠ACD;∠BCD 8.4,DAB,5
9.15°,15°或52.5°,127.5°
10.如果两个角是同一个角的余角,那么这两个角相等.
二、11.D 12.C 13.A 14.C 15.C 16.B 17.A
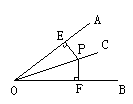 三、18.已知:OC平分∠AOB,P是OC上任意一点,
三、18.已知:OC平分∠AOB,P是OC上任意一点,
PE⊥OA,PF⊥OB,垂足分别是E、F.
求证:PE=PF.
四、19.AD=6.5cm,AN=4.25cm
20.∠C=60° 21.∠PAG=12°
22.∵EF∥AD ∴∠AGE=∠BAD,∠E=∠DAC ∵AD平分∠BAC
∴∠BAD=∠DAC ∴∠AGE=∠E
23.∵EF∥CD ∴∠BEF=∠BCD,∠FED=∠EDC ∵DE∥AC
∴∠EDC=∠DCA ∴∠FED=∠DCA ∵CD平分∠ACB ∴∠DCA=∠BCD
∴∠BEF=∠FED,即EF平分∠BED.