七年级数学（下）《三角形》测验试卷
班级 姓名：_____ _____ 分数：______ ___
一、 选择题：（每小题2分，本题满分20分）
1．下列长度的三条线段可以组成三角形的是 （ ）
（A） 3 4 2 （B）12 5 6 （C）1 5 9 （D）5 2 7
2. 一个三角形的三个内角中，至少有 （ ）
（A） 一个锐角 （B）两个锐角 （C） 一个钝角 （D）一个直角
3. 具备下列条件的两个三角形中，不一定全等的是 ( )
(A) 有两边一角对应相等 (B) 三边对应相等
(C) 两角一边对应相等 （D）有两边对应相等的两个直角三角形
4．适合条件2∠A=2∠B=∠C的三角形是 （ ）
（A）直角三角形 （B）锐角三角形
（C）钝角三角形 （D）不能确定
5．一个三角形的两边分别是4和9，而第三边的长为奇数，则第三边的长是 （ ）
（A）3或5或7 （B）9或11或13
（C）5或7或9 （D）7或9或11
6．能使两个直角三角形全等的条件是 （ ）
（A） 两直角边对应相等 （B） 一锐角对应相等
（C） 两锐角对应相等 （D） 斜边相等
7．已知△ABC≌△DEF，∠A=70°，∠E=30°，则∠F的度数为 （ ）
（A） 80° （B） 70° （C） 30° （D） 100°
8．对于下列各组条件，不能判定△
≌△
的一组是
（ ）
（A） ∠A=∠A′，∠B=∠B′，AB=A′B′
（B） ∠A=∠A′，AB=A′B′，AC=A′C′
（C） ∠A=∠A′，AB=A′B′，BC=B′C′
（D） AB=A′B′，AC=A′C′，BC=B′C′
9．如图，△ABC≌△CDA，并且AB=CD，那么下列结论错误的是 （ ）
（A）∠DAC=∠BCA （B）AC=CA A
D
（C）∠D=∠B （D）AC=BC
10．如图，D在AB上，E在AC上，且∠B=∠C，
则在下列条件中，无法判定△ABE≌△ACD的是（ ）B B
C
（A）AD=AE
（B）AB=AC D
（C）BE=CD
（D）∠AEB=∠ADC
A E C
二、 填空题：（每空2分，本题满分30分）
1、 在△ABC中，∠A=30°,∠C=90°,则∠B=__ __.
2、在△ABC中，∠A=50°,∠B=∠C，则∠B=_____ ___.
3、在△ABC中，∠A：∠B：∠C=2：3：4，则∠A=__ ____
4、三角形有两条边的长度分别是5和7，则第三条边
的取值范围是___________。
|
思考过程：CE⊥AB，DF⊥AB
| ||||||
|
| |||||
|
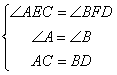
∠AEC=∠BFD=90° AC∥DB
（ ） （ ）
|
△AEC≌（
） （
）
|
|
6、已知如图，∠B=∠DEF，AB=DE，要说明△ABC≌△DEF，
（1）若以“ASA”为依据，还缺条件 .
|
|
|
|
7、把正方形网格分割成两个全等图形，沿虚线画出四种不同的分法：
 | | | |
8、下图是三个等边三角形，请分别把他们分成两个、三个、四个全等的三角形：
 | | ||||
 | |||||
三、 作图题：（每题6分，共12分）
1．如图，画出△ABC的三条高。（用铅笔、三角板画）
C
A B
2．巳知：线段、
，∠
。求作：△ABC，使BC=，AB=，∠ABC=∠（保留作图痕迹，不用写作法）
 |
四、解答题：（每题7分，共28分）
1． 已知：AB⊥BC，AD⊥DC，∠1=∠2，问：BC=CD吗？说明理由。
.
A
1 2
B
D
C
2．△ABC是一个钢架，AB=AC，AD是连结点A与BC中点D的支架。那么AD⊥BC吗？请说明理由。
A
B D C
3． 已知：AD∥BC，AD=CB，AE=CF，请问∠B=∠D吗？为什么？
A
D
E
F
B C
4．已知：点C是AB的中点，CD∥BE，且CD=BE。问：△ACD≌△BCE吗？图中还有其他相等的结论吗？若有，把他们都写出来。
A
C
D
B E
五、知识应用（本题10分）
如图,在一小水库的两侧有A、B两点，A、B间的距离不能直接测得，请用自己学过的知识或方法设计测量方案，求出A、B两点的距离（说明设计方案及理由，并画出草图）。
 |