涪陵区2002-2003学年度测试
初一数学试卷
(满分100分,90分钟完卷)
一、填空题:(每小题3分,共30分)把每小题的正确答案填的各题对应的横线上。
1、有资料表明:被称为“地球之肺”的森林正以每年公顷的速度从地球上消失,每年森林的消失量用科学记数法表示应是 公顷。
2、已知方程![]() 是二元一次方程,那么
是二元一次方程,那么![]() =
,
=
,![]() =
。
=
。
3、若![]() ,则
,则![]() =
,
=
,![]() =
。
=
。
4、12.160= 0 / 〃。
5、若![]() 是方程组
是方程组![]() 的解,则
的解,则![]() =
,
=
,![]() =
。
=
。
6、如图一,OA⊥OC,OB⊥OD,若∠AOB=250,则∠DOC= 0。


7、如图二,![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,∠1=1100,则∠2=
0,∠3= 0。
,∠1=1100,则∠2=
0,∠3= 0。
8、若![]() 的解集为空集,则
的解集为空集,则![]() 与
与![]() 的大小关系是
的大小关系是![]()
![]() 。
。
 9、你喜欢吃拉面吗?拉面馆的师傅,用一根很细的面条,把两头捏合在一起拉伸,再捏合,再拉伸,反复几次,就把这根很细的面条拉成了许多细的面条,如图三所示,这样捏合到第 次时可拉出64根细面条。
9、你喜欢吃拉面吗?拉面馆的师傅,用一根很细的面条,把两头捏合在一起拉伸,再捏合,再拉伸,反复几次,就把这根很细的面条拉成了许多细的面条,如图三所示,这样捏合到第 次时可拉出64根细面条。
10、如图四中的四个图形每个均由六个相同的正方形组成,折叠后能围成正方形的是( )。




二、选择题:(每小题3分,共30分)各小题只有唯一一个正确答案,请将正确答案的字母代号填在本题的答题框内。
1、如果![]() 是正数,那么
是正数,那么![]() 是( )
是( )
A、正数 B、非负数 C、不等于零的数 D、负数
2、如果![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A、![]() >2 B、
>2 B、![]() ≤2
C、
≤2
C、![]() ≥2 D、
≥2 D、![]() <2
<2
3、如图五,线段AD上有两点B、C,则图中共有线段( )
A、三条 B、四条 C、五条 D、六条
![]()
4、若两个角的一边在同一条直线上,另一边相互平行,那么这两个角的关系是( )
A、相等 B、互补 C、相等或互补 D、不能确定
5、三个连续正整数的和小于15,这样的正整数组共有( )
A、一组 B、二组 C、三组 D、四组
6、不等式组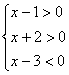 的解集为( )
的解集为( )
A、![]() >-2
B、1<
>-2
B、1<![]() <3
C、
<3
C、![]() <3 D、-2<
<3 D、-2<![]() <3
<3
7、下列运算错误的是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
8、直线![]() 外有一点A,A到
外有一点A,A到![]() 的距离为3cm,P为直线
的距离为3cm,P为直线![]() 上任意一点,则( )
上任意一点,则( )
A、AP>3 B、AP≥3 C、AP=3 D、AP<3
9、若![]() 的值为7,则
的值为7,则![]() 的值为( )
的值为( )
A、0 B、24 C、34 D、44
10、小明在生日宴会上,要把一个大蛋糕分成七块,问他最少要切几次(切割成的蛋糕面积不一定相等)( )
A、3次 B、4次 C、5次 D、6次
三、解答题(每小题6分,共18分)
1、解方程:![]()
2、解方程组: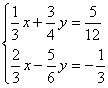
3、解不等式组,并把解集表示在数轴上。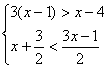
四、先化简,再求值。(6分)
当![]() =-2时,求代数式
=-2时,求代数式![]() 的值。
的值。
五、如图六,推理填空(6分)
 (1)∵∠B=
(已知)
(1)∵∠B=
(已知)
∴DE∥BC( )
(2)∵∠3+ =1800
∴DE∥BC( )
(3)∵∠4= (已知)
∴AB∥EC ( )
(4)∵AB∥ (已知)
∴∠1=∠E( )
(5)∵ ∥ (已知)
∴∠2+∠E=1800( )
(6)∵ ∥ (已知)
∴∠3=∠6( )
六、(10分)某商场计划拨款9万元从厂家购进50台电视机。已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元。
(1)若商场同时购进其中两种不同型号电视机共50台,用去9万元,请你研究一下商场的进货方案有几种;
(2)若商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元,在同时购进两种不同型号电视机的方案中,为使销售获利最多,你选择哪种进货方案?
(3)若商场准备用9万元同时购进三种不同型号的电视50台,请你设计进货方案。
参考答案
一、填空题:
1、1.5×107;2、![]() =3、
=3、![]() =2;3、
=2;3、![]() =2、
=2、![]() =-3;4、
=-3;4、![]() ;5、
;5、![]() =2、
=2、![]() =3;6、250;7、1100、700;8、
=3;6、250;7、1100、700;8、![]() ≥
≥![]() ;9、6;10、C
;9、6;10、C
二、选择题:CDDCC,BCBCA
三、解答题:
1、解方程:![]()
解:![]() (1分)
(1分)
![]() (2分)
(2分)
![]() (3分)
(3分)
![]() (4分)
(4分)
![]() (5分)
(5分)
![]() (6分)
(6分)
2、解方程组:
解:将原方程组整理得:![]() (2分)
(2分)
![]() (3分)
(3分)
![]() ③
(4分)
③
(4分)
把![]() 代入①得:
代入①得:![]() (5分)
(5分)
∴![]() (6分)
(6分)
3、解不等式组,并把解集表示在数轴上。
解:不等式①的解集为:![]() >-
>-![]() (2分)
(2分)
不等式②的解集为:![]() >4
(4分)
>4
(4分)
∴原不等式组的解集为:![]() >4
(5分)
>4
(5分)
这个不等式组的解集在数轴上表示如下:

四、先化简,再求值:
解:原式=![]() (2分)
(2分)
=![]() (4分)
(4分)
当![]() =-2时,原式=
=-2时,原式=![]() (5分)
(5分)
=-14 (6分)
五、如图六,推理填空(如图)
 (1)∵∠B= ∠1 (已知)
(1)∵∠B= ∠1 (已知)
∴DE∥BC(同位角相等,两直线平行)
(2)∵∠3+ ∠5 =1800
∴DE∥BC(同旁内角互补,两直线平行)
(3)∵∠4= ∠A (已知)
∴AB∥EC (内错角相等,两直线平行)
(4)∵AB∥ CE (已知)
∴∠1=∠E(两直线平行,内错角相等)
(5)∵ AB ∥ CE (已知)
∴∠2+∠E=1800(两直线平行,同旁内角互补)
(6)∵ DE ∥ BC (已知)
∴∠3=∠6(两直线平行,同位角相等)
六、(10分)
解:设商场需购进甲种电视机![]() 台,乙种电视机
台,乙种电视机![]() 台,丙种电视机
台,丙种电视机![]() 台。
台。
(1)根据题意得:![]() (1分)
(1分)
![]() (1分)
(1分)
![]() (1分)
(1分)
解得:![]() (1分)
(1分)![]() (1分)
(1分) ![]() (舍去)(1分)
(舍去)(1分)
∴ 只有两种进货方案。方案一:甲种25台,乙种25台;方案二:甲种35台,丙种15台。
(2)∵ 方案一可获利:25×150+25×200=8750(元) (1分)
方案二可获利:35×150+15×250=9000(元) (1分)
∴ 购甲种电视机35台,丙种电视机15台时获利最多。
(3)根据题意得:![]()
由①得:![]() =
=![]() ③
③
把③代入②整理得:![]()
又由于![]() 、
、![]() 、
、![]() 均为正整数
均为正整数
∴ ![]() =5、
=5、![]() =10、
=10、![]() =15、
=15、![]() =20
=20
∴ 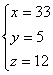
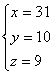
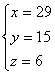

∴ 共有四种进货方案,它们是:
方案一:购甲种电视机33台,乙种电视机5台,丙种电视机12台;(1分)
方案二:购甲种电视机31台,乙种电视机10台,丙种电视机9台;(1分)
方案三:购甲种电视机29台,乙种电视机15台,丙种电视机6台;(1分)
方案四:购甲种电视机27台,乙种电视机20台,丙种电视机3台;(1分)