第四届“华罗庚金杯”少年数学邀请赛
初赛试题
复赛试题
决赛第一试
决赛第二试
团体决赛口试
初 赛
（1）请将下面算式结果写成带分数：
[分析] 这是每位小学生都会算的题目，但初赛要求在30秒内计算出正确的结果，就需要在平时锻炼快算的技巧。注意 0.5乘 236之积为 118，仅比分母小1。抓住这个特点，算起来便很快了。
[注] 华罗庚爷爷在四十年代给他的孩子出了一道题：“全家九口人，每人每日食半两油，问全家一个月30天要食几斤油？”当时一斤等于16两。快速心算的思路是：每人一月食15两油，即一斤少一两。全家九口人，一月食9斤少9两，即8斤7两。列成算式是
本题便是根据华爷爷的问题改编而成的。
（2）一块木板上有13枚钉子（右图）。用橡皮筋套住其中的几枚钉子， 可以构成三角形，正方形，梯形，等等（下图）。请回答：可以构成多少个正方形？
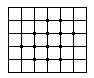
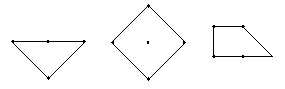
[答案]共11个。
[分析]可以构成的正方形有好几种，大小和位置不一样。要想无一遗漏地数出全部正方形，最好用分类法。
[解]依正方形的面积分类，设最小的正方形面积为1。
面积为1的正方形，有5个（图a）；
面积为2的正方形，有 4个（图b）；
面积为4的正方形，有1个（图c）；
还有1个面积比4大的正方形（图d）。
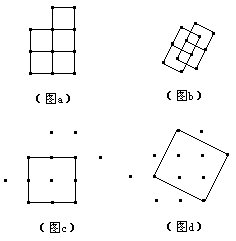
[讨论]本题也可以按其他特征来分类。例如按正方形各边的方向的特征，如果各边是水平和竖直方向的，有6个（图a和图c）；各边都是倾斜的有5个（图b和图d）。
用分类法的关键是抓住事物的特征，给列举的类排序。既要穷尽所有的可能性，以避免遗漏，又要注意每二类之间是否有共同的部分，如果有，则需要加以排除。
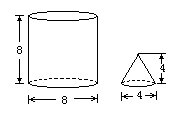
（3）这里有一个圆柱和一个圆锥（下图），它们的高和底面直径都标在图上，单位是厘米。请回答：圆锥体积与面积的比是多少？
[分析]这是一道普通的体积计算题。相信同学们都能记住圆柱和圆锥的
比，π可以消去，再把各自的底面半径和高代入公式便行了。
列，排在中间的是哪个数？
[分析]要比较分数大小，通常的做法是先通分，再比较分子的大小，这道题目的5个分母通分，公分母是个很大的数，算起来便复杂了。我们可以换个方式：将5个分数的分子换成相同的数，再比较分母的大小。也就是说，先找出分子的最小公倍数，再将这些分数进行等值变换。
[解]分子的最小公倍数是60。给出的5个分数依次等于：
[注]把这道题放在初赛中，目的是测验同学们快算技巧和灵活性。如果按通常先找分母最小公倍数的做法，就不可能在60秒钟内解答完。
（5）现在流行的变速自行车，在主动轴和后轴分别安装了几个齿数不同的齿轮。用链条连接不同搭配的齿轮，通过不同的传动比获得若干档不同的车速。
“希望牌”变速自行车主动轴上有三个齿轮，齿数分别是48，36，24；后轴上有四个齿轮，齿数分别是36，24，16，12。问：“这种变速车一共有几档不同的车速？
[答案]8档。
[分析]传动比=主轴齿轮齿数∶后轴齿轮齿数。例如主轴齿轮48齿，后轴齿轮16齿，传动比=48∶16=3，也就是说如果主轴转一圈，轮子转3圈。这道题目实际上是要求算出所有的传动比，再看看有几个不同的。
[解法]算出全部传动比，并列成表：
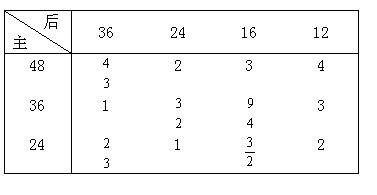
将重复的传动比去掉，剩下8个不同的比，所以有8档不同的车速。
[讨论]现实生活中处处都有美妙的数学问题，本题只是一个例子。出这道题的用意就是鼓励同学们留心注意周围的事物，并用课堂中学到的知识，去解决实际问题。
对于爱动脑筋，喜欢寻根问底的同学，大概不会满足于懂得解答本题。他们也许会去找一辆真正变速车，实地数一数主轴和后轴齿轮的齿数。他们会发现，这里边还有许多更有趣的数学问题哩！
有一辆12速的山地车（实物），它的主轴有3个齿轮，齿数分别是48，38，28；后轴有6个齿轮，齿数分别是28，24，20，18，16，14。如果按刚才的解法，列出下面的传动比：
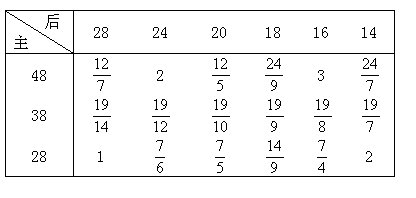
其中重复的传动比只有1个（2），去掉它，这辆车应该有17档不同的车速，为什么叫12速山地车？
为了解答这个疑问，我们还可以做一些数学上的分析。先将算出的传动比都化成小数，并保留小数后二位（四舍五入）：
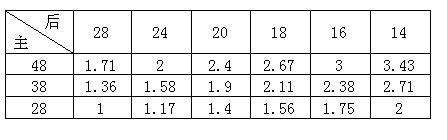
任意2个传动比，如果它们相差小于0.05，将被看成是近似地相同的。上表中的2.71与2.67；2.38与2.4；1.75与1.71；1.56与1.58；1.4与1.36；相差都不大于0.04，这5对传动比作用差不多，可以看作近似地相同。将重复的去掉，便只剩下12档不同的车速了。
有些年青人到商店买自行车，总希望车速越多越好。车速越多，价格就越昂贵。有些商店为迎合顾客的心理，将刚才分析的山地车标以“18速山地车”。你问他们为什么是18速，他们会振振有词地说：3乘6等于18嘛！如果你懂得点数学知识，你大概就不会上当。你也不会多花好多钱，去买一辆名义上许多档、实际上并非如此的昂贵自行车了。
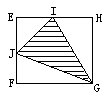
（6）右图中的大正方形ABCD的面积是 1，其它点都是它所在的边的中点。请问：阴影三角形的面积是多少？
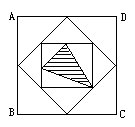
[解法]将小正方形各顶点标上字母如右图，很容易看出三角形JFG面积=
（7）在右边的算式中，被加数的数字和是和数的数字和的三倍。问：被加数至少是多少？
[答案]18
[分析]从“被加数的数字和是和数的数字和的三倍”这句话，可以推断出两点：①被加数可以被3整除，和数也可以被3整除；②在加法运算时，个位数相加一定有进位，否则和数的数字和只会增加。
[解法]因为个位数相加必有进位，所以被加数的个位数只可能是7，8或9。又出为被加数是3的倍数，它只能是下面几种情形：
个位数是7，被加数可能是27，57，87，经验算，27满足题目要求。
个位数是8，被加数可能是18，48，78，经验算，18满足要求。
个位数是9，被加数可能是39，69，99，都不满足题目要求。
因此，满足题目的最小的被加数是18。
（8）筐中有60个苹果，将它们全部都取出来，分成偶数堆，使得每堆的个数相同。问：有多少种分法？
[答案]8种。
[分析]“每堆个数相同”和“偶数堆”二个条件合起来，就是要求60的偶因子的个数，因为每个偶因子对应于一种符合条件的分法。
[解法1]直接列举出 60的偶因子：2， 4， 6， 10，12，20，30，60。共8个。
[解法2] 60的偶因子个数与30的因子个数相同。 30=2×3×5。所以因子个数为：（1+1）×（1＋1）×（1+1）＝8。
（9）小明玩套圈游戏，套中小鸡一次得9分，其中小猴得5分，套中小狗得2分。小明共套了10次，每次都套中了，每个小玩具都至少被套中一次。小明套10次共得了61分。问：小鸡至少被套中多少次？
[答案]本题的解法看来没有太多技巧，只能用试凑法。因为问小鸡至少被套中多少次，很自然会想到从多往少地试小鸡被套中的次数。
[解法1]设小鸡被套中次数为x。
x不能多于6，否则得分超过了61分。
x=6，套中小鸡得分为 6×9=54，余下 4次套小猴和小狗，得分最少的情况是套中小猴1次，小狗 3次，得 5＋2×3=11分。总得分 65，超过 16分， 所以不可能套中小鸡6次。
x=5，套中小鸡5次得45分。余下5次套小猴和小狗应该得16分。如果套中小猴2次得10分，套中小狗3次得6分，符合要求。
因此，小明至多套中小鸡5次。
[解法2]设套中小鸡x次，套中小猴y次，那么套中小狗（10-x-y）次。得分为61分，所以
9x+5y+2（10-x-y）=61
化简后得 7x=41-3y。
显然y越小，x越大。将y=1代入得7x=38，无整数解。若y= 2，7x=35，解得x=5。因此，小明至多套上小鸡5次。
（10）车库中停放若干辆双摩托车和四轮小卧车，车的辆数与车的轮子数之比是2∶5。问：摩托车的辆数与小卧车的辆数之比是多少？
[答案]3∶1
[解法1]车库中，平均每2辆车有5个轮子。也就是说，平均每4辆车有10个轮子。用简单的试凑法可以知道，1辆小卧车和3辆摩托车恰好是10个轮子。所以摩托车的辆数与小卧车的辆数之比为3∶1。
[解法2]设有摩托车x辆，小卧车y辆。由题意
[讨论]本题其实是换一种形式描述的“鸡兔同笼”问题，而且只是求二种车数之比。解法2是鸡兔同笼问题的列方程解法，在一般情况下都适用。解法2中用试凑法，解本题时很方便，不懂得解方程的学生容易理解。即使给出的数字变得复杂些，也不难算出结果。例如在本题中，设车的辆数与车轮子数之比是41∶99，怎么算？
平均每82辆车有198个轮子。
0辆小卧车和82辆摩托车共164个轮子。
每增加1辆小卧车（相应减少1辆摩托车），增加2个轮子。
（198-164）÷2=34÷2=17（小卧车）。
82-17=65（摩托车）。
摩托车辆数与小卧车辆数之比是65∶17。
（11）有一个时钟，它每小时慢25秒，今年3月21日中午十二点它的指示正确。请问：这个时钟下一次指示正确的时间是几月几日几点钟？
[答案]1993年6月1日中午12点钟。
[解]当这个时钟总共慢12个小时的时候，它又指示12点，恰好是准确的时间。先求出多少小时后慢12个小时。因为每小时慢 25秒，而 1小时=60 ×60秒。
再求出它相当于多少天：
最后求出3月21日后的72天是几月几日？注意3月份有31天，4月份有30天，5月份有31天，到6月1日中午，恰好是72天。
（12）某人由甲地去乙地。如果他从甲地先骑摩托车行12小时，再换骑自行车9小时，恰好到达乙地。如果他从甲地先骑自行车行21小时，再换骑摩托车行8小时，也恰好到达乙地。问：全程骑摩托车需要几小时到达乙地？
[答案] 15小时。
[分析]在分析行程问题时，一般部是在草稿纸上先画出粗略的示意图。本题给出的两种行进方式是
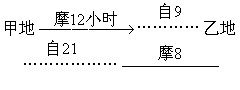
可以看出：摩托车走12-8＝4小时的路程，自行车要用21-9=12小时。这就是解题的关链。如果我们将第二次行进方式次序改一下，与第一次作比较，就可以看得更清楚了：
[解]摩托车是12-8=4小时的路程，自行车要用21-9=12小时。摩托车走完全程需要
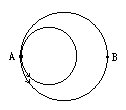
（13）下图的二个圆只有一个公共点A，大圆直径48厘米，小圆直径30厘米。二只甲虫同时从A点出发，按箭头所指的方向以相同速度分别沿二个圆爬行。问：当小圆上的甲虫爬了几圈时，二只甲出相距最远？
[答案]4圈。
[分析]圆内的任意两点，以直径两端点的距离最远。如果沿小圆爬行的甲虫爬到A点，沿大圆爬行的甲虫恰好爬到B点，二甲虫的距离便最远。小圆周长为π×30=30π，大圆用长为48π，一半便是24π。问题便变为求30π和24π的最小公倍数问题了。
30π和24π的最小公倍数，相当于30与24的最小公倍数再乘以π。
[解法] 30与24的最小公倍数是120，
120÷30＝4
120÷24＝5。
（14）某种少年读物，如果按原定价格销售，每售一本，获利0.24元；现在降价销售，结果售书量增加一倍，获利增加0.5倍。问：每本书售价降价多少元？
[答案]降低0.06元。
（元），每本获利0.18（元），所以每本书售价降低0.24-0.18=0.06（元）。
（15）有一座四层楼房，每个窗户的4块玻璃分
别涂上红色和白色，每个窗户代表一个数字。每层楼有三个窗户，由左向右表示一个三位数。四个楼层表示的三位数有：791，275，362，612。问：第二层楼表示哪个三位数？
[答案]612。
[分析]一个窗户相当于代表一个数字的符号，从给出的条件设法推断出每个符号代表什么数字，便可以回答本题了。
[解]给出的4个数中362和612个位数相同，第二和第四层右边窗户符号也相同，可以肯定这两层分别代表362和612。这二个数中又有数字6是一样的，对照第二层和第四层的窗户，进一步确定第二层代表612（同样，很容易确定每层所代表的数字）。
复 赛
（1）化简
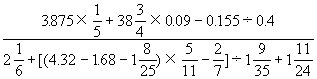
所以，原式等于1。
[注]本题与第三届“华杯赛”复赛第一道参考试题性质近似。
解这类题时，在乘、除运算中，小数宜写成分数、代分数宜化成假分数并将运算结果及时约分；在加、减运算中，当小数、分数都出现时，通常宜于都化为分数，因为，分数化为小数时，有可能出现无限循环小数；当然，在能都化成有限小数时，也可以都化为小数。
（2）电视台要播放一部30集电视连续剧。如果要求每天安排播出的集数互不相等，该电视连续剧最多可以播几天？
[分析]由于希望播出的天数尽可能地多，所以，在每天播出的集数互不相等的条件下，每天播放的集数应尽可能地少。
我们知道，1+ 2＋3+ 4＋5＋6＋7= 28。
所以，如果各天播出的集数分别为1，2，3，4，5，6，7时，这七天共可插出28集，还剩2集未播出。由于已有过一天播出2集的情形，因此，这余下的2集不能再单独于一天播出，而只好把它们分到以前的日子，通过改动某一天或某二天播出的集数，来解决这个问题。例如，各天播出的集数安排为1，2，3，4，5，7，8或1，2，3，4，5，6，9都可以。
[答]最多可以播7天。
[注]本题实际上是问，把正整数30分拆成互不相等正整数之和时，最多能写成几项之和？也可以问，把一个正整数拆成若干个正整数之和时，有多少种分拆的办法？例如：5=1＋1＋1＋1＋1=1＋1＋1＋2=1＋2＋2=1＋1＋3=2＋3=1＋4共6种分拆法（不计分成的整数相加的顺序）。
（3）一个正方形的纸盒中，恰好能放入一个体积为628立方厘米的圆柱体，纸盒的容积有多大？（圆周率=3.14）。
[分析]由于是正方形纸盒，所以它的长、宽、高相等。又因为圆柱体“恰好”能放入，所以圆柱体的高等于纸盒的高，而后者又与圆柱体底面的直径相等。从而，圆柱体的体积V既等于6.28立方厘米，又等于3.14×（底面半径）2×2倍的底面半径=6.28×（底面半径）3立方厘米由此可见，圆柱的底面半径等于1（厘米），从而底面直径等于2厘米，由此即知纸盒的容积是2×2×2=8立方厘米。
[答]纸盒的容积是8立方厘米。
（4）有一筐苹果，把它们三等分后还剩2个苹果，取出其中两份，将它们三等分后还剩2个；然后再取出其中两份，又将这两份三等分后还剩2个，问：这筐苹果至少有几个？
[分析]我们面对着最后剩下的2个苹果，它们是把某两份苹果三等分后剩下的。换句话说，把所剩的2个苹果与三等分的三份苹果放在一起，应是上一轮分割中的两份。所以这个总数必须能被2整除。题中又问这筐苹果“至少”有几个，从而上述总数又应尽可能地少。三份苹果中，每份最少有1个苹果，于是三份便是3个。2＋3= 5，但5不被2整除，所以每份不应只有一个苹果。退而求其次：设三份苹果中每份是2个，从而三份共6个，2＋6= 8，于是可设上一轮中共有2＋3×4=14个苹果。14个又是第一轮分割时三等分所得的2份，从而依题义，最初的苹果应有 2＋3×7=23个。
[解]用倒推法可见，原有苹果数是
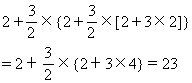
[答]这筐苹果至少有23个。
[注]用倒推法还可以解决比本题复杂一些的类似的问题。例如，每次所剩的苹果数不都是2而是互相有所不同；每次也不一定三等分，等等。大家不妨自行编题去试。
（5）计算
[解]原式
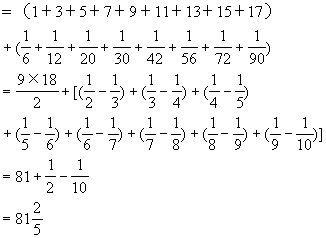
[注]本题的规律性很强。只要能观察出每项的整数部分形成等差数列，
（6）长方形 ABCD周长为16米，在它的每条边上各画一个以该边为边长的正方形，已知这四个正方形的面积和是68平方米，求长方形ABCD的面积
[解] 如图，将A1D1 向右延长，C1E1向上延长，交于E点，那么正方形A1BC1E的面积，等于长方形 ABCD周长一半的平方。即64平方厘米。
长方形 ABCD与 D1DE1E是全等的。而正方形 A1ADD1与 DCC1E1的面积之
米。64-34= 30平方厘米应等于长方形 ABCD面积的 2倍。所以 ABCD 的面 
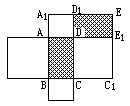
[注] 本题的解法，可算作求面积的“割补法”。
（7）“华罗庚”金杯少年数学邀请赛，第一届在1986年举行，第二届在1988年举行，第三届是在1991年举行，以后每2年举行一届。第一届“华杯赛”所在年份的各位数字和是
A1＝1＋9＋8＋6＝24。
前二届所在年份的各位数字和是
A2=1＋ 9＋ 8 ＋ 6 ＋1＋ 9＋ 8 ＋ 8=50
问：前50届“华杯赛”所在年份的各位数字和A50＝？
[分析]这是一次“跨世纪”的计算。
按所给的规律，在20世纪内有7次赛事，前50届在21世纪内于是有43次赛事。
在 20世纪内，已知A2= 50，其余 5届年份各位数字的和是
5×（1＋9）＋5×9＋（1＋3＋5＋7＋9）
=50＋45＋25=120
从而A7=A2＋120=170
在 21世纪内的前5届年份各位数字和是2×5＋25=35。接下去的每5届递加数字5（因为年份的十位数字各增了1），于是前47届年份各位数字的和等于
170＋35+40＋45＋50＋55＋60＋65＋70
＝170＋4×105＝590
再加上前50届中最后三届年份的各位数字的和：2×3＋8×3＋（1＋3＋5）=6＋24＋9=39。得A50＝ 590+39=629。
[答] A50=629
[注]以上的分析与计算，主要用了分段处理问题的想法，例如分“世纪”作考虑，并且分“年代”作考虑。在计算中，主要依据了整数相加有交换律，可以把相同的项调集在一起计算，以便用乘法代替连加。
（8）将自然数按如下顺次排列：
1 2 6 7 15 16 …
3 5 8 14 17 …
4 9 13 …
10 12 …
11 …
在这样的排列下，数字3排在第二行第一列，13排在第三行第三列，问：1993排在第几行第几列？
[分析]我们来分析一下给出阵列中每一斜行的规律。这里第2斜行的数字是3，2；第3斜行的数字是4，5，6；余此类推。仔细观察后我们会发现：
奇数斜行中的数字由下向上递增；
偶数斜行中的数字由上向下递增。
如果我们找出1993位于斜行的第几位，再换算成原阵列中的第几行第几列，问题便解决了。
[解]经试算，第62斜行中最大的数字是
第63斜行中最大的数字是2016。所以 1993位于第63斜行。第63斜行中数字是由下向上递增加，左边第一位数字是1954，因此，1993位于第63斜行由上向下数第（1993-1954+1）=40位。换算为原阵列的行和列，便是第（63-43+1）=24行，第40列。
[答]1993排在第 24行，第 40列。
（9）在下图中所示的小圆圈内，试分别填入1、2、3、4、5、6、7、8这八个数字，使得图中用线段连接的两个小圆圈内所填的数字之差（大数字减小数字）恰好是1、2、3、4、5、6、7这七个数字。
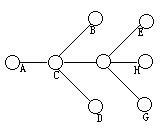
[分析]把连接小圆圈的线段叫作边，把小圆圈称作这个边的端点。同一个边的两个端点，叫作相邻的端点，当小圆圈内填入某数字k时，便用k来记它，把两个端点所填数字之差（大数字减小数字）称为它们之间的边的“标号”。那么，标号为1的边和它的端点，可能有：①-②，③-③，③-④，④-⑤，⑤-⑥，⑥-⑦，⑦-⑧；标号为2的边和它的端点，可能有：①-③，②-④，③-⑤，④-⑥，⑤-⑦，⑥-⑧；标号为3的边和它的端点，可能有：①-⑤，②-⑥，③-⑦，④-⑧，标号为5的边和它的端点，可能有：①-⑥，②-⑦，③-⑧，标号为6的边和它的端点，可能有：①-⑦，②-⑧，标号为7的边和它的端点是：①-⑧，可见，①与⑧必是相邻的端点，由上可见，⑧可以是任何标号的边的端点，所以，选择邻点最多的点，例如C，作⑧似乎是自然的。但，这时F不能取作①，因为如果这样，以①（即F）为一个端点而尚未加标号的边还有三条，它们地位是对称的， 在1、2、3、4、5、6中，无论取哪三个作它们的标号，都会得到矛盾。例如，取作标号的数为1、3、6，则与 F相邻的点除 C外，就是②、④、⑦，剩下未标号的边，其标号只能取2、4、5，于是与C（即⑧）相邻的点便应是③、④、⑥。这里出现了④的重复出现，这是矛盾。所以，应取A、B、D之一为①，由对称性，不妨取A为①。还有三个与C相邻的点： B、 D、 F。其中， F的地位与B、D不同。仿上可知，在F处不能是③。⑤、⑥、⑦。取F为④，令以 F为一端点的未标号的边的标号为1、2、3，从而以C为一端的、余下未标号的两条边的标号便应是5、 6、这样便可得B= ③， D= ②， E= ⑦，G= ⑤，H= ⑥。
[答] 在 A、B、C、D、E、F、H处，顺次在小圆圈内填入1、3、8、2、7、4、5、6便可满足要求。
[注]满足题目要求的图，叫作“优美图”。本题是一个至今尚未解决的猜想的一个特殊的例子。
本题的答案不止一种。例如：
A（1）、B（6）、C（8），D（4），E（3），F（2），G（7），H（5）；又如：
A（8），B（6），C（1），D（7），E（2），F（5），G（3），H（4）等等都是。
由于C与F的地位，A、B、D的地位，E、G、H的地位分别都是对称的，所以，当相邻关系不变时，填在C、F处的，A、B、D处的以及填在E、G、H处的数字可以分别交换，而这样得到的结果并无实质上的区别。请想一想：有多少种既满足题目要求又实质上不同的填法？
（10）11＋ 22＋ 33＋ 44＋ 55＋ 66＋ 77＋ 88＋ 99除以3的余数是几？为什么？
[分析]上式各加项中，33、66、99除以3余数得0，所以只须看表达式11+22＋44＋55＋77＋88除以3余几，任何不是3的倍数的自然数，必可表为3k＋1或3k＋2，其中k是某个非负整数，而（3k＋1）2=9k2＋6k＋1，（3k＋2）2=9k2＋12k+3＋1。可见，不是3的倍数的自然数的平方，除以3余数都是 1，即都可表为3的某个倍数加 1。今11=1， 22=4=3＋1，44=（42）2=3M1＋1， 55=（52）2·5=（3m2+1）（3+2）＝9 M2+3＋6m2+2=3m2＋2， 77＝（73）2·7＝（3M4＋1）（6＋1）=3M5＋1，88=（84）2=3M6＋1，总上可见，原式除以 3的余数，是 1＋1＋1＋2＋1＋1=7除以3的余数，所以余数是1。
[答]余数是1。
（11） A、 B、 C、 D、 E、 F六个选手进行乒乓球单打的单循环比赛（每人都与其他选手赛一场），每天同时在三张球台各进行一场比赛，已知第一天B对 D，第二天 C对E，第三天 D对 F，第四天B对C，问：第五天A与谁对阵？另外两张球台上是谁与谁对阵？
[分析]我们在平面上分别画上6个点，依次用它们代表选手A，B，C，D，E，F，将给定的比赛对阵用二点的连线来表示（右图，连线上的数字表示第几天。
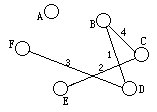
注意到每位选手每天恰赛一场，每对选手之间5天内也恰赛一场。第二天A不可能与F对阵，否则当天E要对C，而他们之间的比赛已安排在第2天。
所以第一天只能是A-E和C-F，或是A-C，E-F。这次逐天分析推理，一定可以得出本题的答案。
[解]逐天分析可能的对阵情况，列成下表：
[答]第五天A与B对阵，另2张球台上的
对阵是C对D，E对F。
[注]这是道很有意思的逻辑推理题。如果在草图上用不同颜色代表不同天的对阵安排，便能很清楚地从图上推出结论，不必画表。请同学们自己试试看。
（12）有一批长度分别为1、2、3、4、5、6、7、8、9、10和11厘米的细木条，它们的数量都足够多，从中适当选取3根本条作为三条边，可围成一个三角形。如果规定底边是11厘米长，你能围成多少个不同的三角形？
[分析]任何一个三角形，它的三条边中的任何两条边的长度之和，总比余下的一条边要长。换句话说，在本题中底边是11厘米长的三角形的其余二
于是（a、b）的可能的值便有
（11，11）；（10，10），（10，11）；（9，9），（9，10），
（9，11）；（8，8），（8，9），（8，10），（8，11）；
（7，7），（7，8），（7，9），（7，10），（7，11）；
（6，6），（6，7），（6，8），（6，9），（6，10），
（6，11）；（5，7），（5，8），（5，9），（5，10），
（5，11）；（4，8），（4，9），（4，10），（4，11）；
（3，9），（3，10），（3，11）；（2，10），（2，11）；
（1，11）。可见，总数等于2×（1＋2＋3＋4＋5）+6=36。
[答]能围成36个不同的三角形。
[讨论]仿上面的分析，如果木条的长度是从1到10厘米，并规定底边长为10厘米，那么同样问题的答案将如下得出，记号仿前：（a，b）可能的值有：（10，10）；（9，9），（9，10）；（8，8），（8，9），
（8，10）；（7，7）（7，8），（7，9），（7，10）；
（6，6），（6，7），（6，8），（6，9），（6，10）；
（5，6），（5，7），（5，8），（5，9），（5，10）；
（4，7），（4，8），（4，9），（4，10）；（3，8），
（3，9），（3，10）；（2，9），（2、10）；（1，10）所以总数是2×（1＋2＋3＋4＋5）=30。一般情况，当最长细木条的长
（13）把下图a中的圆圈任意涂上红色或蓝色。问：有无可能使得在同一条直线上的红圈数都是奇数？请说明理由。
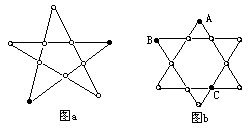
[分析]红蓝二色可以分别更换为数字1与0。
这样作对问题的实质并无影响。
假定题中所设想的涂色方案能够实现，那么每条直线上代表各点的数字之和便应都是奇数。一共有五条直线，所以，把这五条直线上代表各点的数字之和的这五个奇数再加起来，得到的总和数仍是一个奇数。但是，由视察可见，图中每个点都恰好同时位于两条直线上，所以，在求上述总和数时，代表各点的数字都恰被加过两次，所以这个总和应是一个偶数。这就导致一个矛盾。
[答]没有可能。
[讨论]由于每条直线上恰有4个点，所以，也不可能使同一条直线上的蓝圈数都是奇数。可见无论设红色为1蓝色为1，结果都不变。
如果是由偶数条直线构成的类似的图，例如图b，问题中要求的涂色法便有可能实现。比如给A、B、C三点涂红色，其余涂蓝色。
（14）甲、乙二人在同一条椭圆形跑道上作特殊训练：他们同时从同一地点出发，沿相反方向跑，每人跑完第一圈到达出发点后立即回头加速跑第
次相遇点190米，问：这条椭圆形跑道长多少米？
[分析]让我们先画一个示意图（右图），并设一开
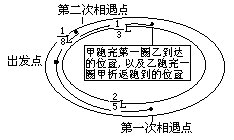
即L=400米。
[答]跑道长为400米。
（15）下图a中的正方形ABCD的面积为1，M是AD边上的中点。求图中阴影部分的面积。
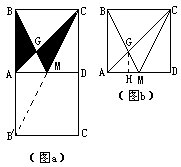
△ABM-△AGM=△ABG。
[注]这是求面积常用的“割补法”的一次具本运用；也可以不用割补法
（16）四个人聚会，每人各带了2件礼品，分赠给其余三个人中的二人，试证明：至少有两对人，每对人是互赠过礼品的。
[证明]设此四人为甲、乙、丙、丁并用画在平面上的四个点分别表示他们，称为它们的代表点，当某人（例如甲）赠了1件礼品给另一人（例如乙）时，就由甲向乙的代表点画一条有指向的线，无非有以下两个可能：
（一）甲、乙、丙、丁每人各收到了2件礼品。
（二）上面的情形不发生。这时只有以下一个可能，即有一个人接受了3件礼品（即多于2件礼品；因为一人之外总共还有三个人，所以至多收到3件礼品）。（或许会有人说，还有二个可能：有人只收到1件礼品及有人什么礼品也没收到。其实，这都可归以“有一人接受了3件礼品”这个情形。因为，当有一人（例如甲）只接受了1件礼品的情形发生时，四人共带来的8件礼品中还剩下7件在甲以外的三个人中分配，如果他们每人至多只收到2件礼品，则收受礼品数将不超过6件，这不可能，所以至少有一人收到2件以上（即3件）礼品，同样，当甲未收到礼品时，8件礼品分给乙、丙、丁三人，也必定有人收到3件礼品）。
当（一）发生时，例如甲收到乙、丙的礼品，由于甲发出的礼品中至少有1件给了乙或丙，为确切计，设乙收到了甲的礼品，于是我们先有了一对人：（甲、乙），他们互赠了礼品，如果丙也收到甲的礼品，那么又有了第二对互赠了礼品的人（甲、丙）；如果收到甲礼品的另一人是丁（如右图）丁的2件礼品必定分赠了乙及丙（甲已收足了本情形中限定的2件札品）丙或乙的另一件礼品 给了丁，则问题也已解决（这时另一对互赠了礼品的人便是（乙、丁）或（丙、丁））但丙的另一件礼品只能给丁，因为这时乙已收足了2件礼品，所以，当本情形发生时，至少能找到两对互赠过1件礼品的人。
当（二）发生时，不失一般性，设甲收到了来自乙、丙、丁的各1件礼品，但甲又应向他们之中的某二人（例如乙、丙）各赠送1件礼品，于是（甲、乙），（甲、丙）便是要找的两对人。总上可知，证明完毕。
[注]像图中所画的这种示意图，叫作“有向图”，是一个数学分支“图论”所研讨的内容之一。
决赛第一试
（1）在100以内与77互质的所有奇数之和是多少？
[解]设A为100以内所有奇数之和，B为100以内与77有非1的公约数的全体奇数之和， X为100以内与77互质的所有奇数之和，因为任一自然数，要么与77互质，要么与77有非1的公约数，所以
X＝A－B （1）
＝2500（2）
77＝7×11（3）
100以内有约数7的奇数之和为
7×（1＋3+5+9+11＋13）
100以内有约数11的奇数之和为
所以 B=343＋275-77＝541 （6）
（6）中减去77是因为在（4）和（5）中都计算过77这一项，最后
X＝2500-541＝1959
[答]和为1959。
[分析与讨论]100以内的奇数有50个，我们将它们分成两组，第一组是与77互质的所有奇数；第二组是与77有非1的公约数的全体奇数。这两个组没有公共的数，将这两个组合并在一起正好就是100以内的全体奇数。这样一来，知道了100以内的全体奇数之和及某一组中全体奇数之和就可以计算出另一组中全体奇数之和了。
（2）图1，图2是两个形状、大小完全相同的大长方形，在每个大长方形内放入四个如图3所示的小长方形，斜线区域是空下来的地方，已知大长方形的长比宽多6cm，问：图1，图2中画斜线的区域的周长哪个大？大多少？
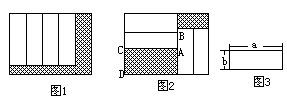
[解]图1中画斜线区域的周长恰好等于大长方形的周长，图2中画斜线区域的周长显然比大长方形的周长小，二者之差是2AB。
从图2的竖直方向看，AB＝a-CD。
再从图2的水平方向看，大长方形的长是a+2b，宽是2b+CD。已知大长方形的长比宽多6cm，所以
（a+2b）-（2b＋CD）＝a-CD
=6cm
因此，图1中画斜线区域的周长比图2中画斜线区域的周长大2AB＝12cm。
[分析与讨论]观察图形的特点，找出几何关系是很重要的，上面的解法中，由图2看出AB＝6cm，进一步又找出图1、图2画斜线的区域周长之差是2AB，这就省去了很多计算的工作量，如果用很多字母把图1，图2中画斜线的区域的周长表示出来，再相减，则要麻烦些。
如果把问题稍微改一下，问图4，图5中画斜线的区域的周长的大小关系。你会回答吗？这时图5中画斜线的区域周长大，你想想，是不是大2EF？
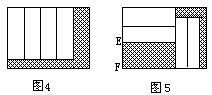
（3）这是一个道路图，A处有一大群孩子，这群孩子向东或向北走，在从A开始的每个路口，都有一半人向北走，另一半人向东走，如果先后有60个孩子到路口B，问：先后共有多少个孩子到路口C？
[解]在A处的孩子数目看成1份，那么可顺次标出各道口处走过的孩子
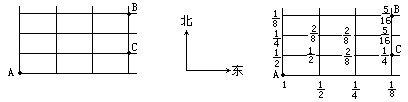
[分析与讨论]如果数一数，可以看出由A到B共有20条路，每条路平均有60÷20＝3（人）走到B。
A到B共走6“步”（向北，向东走一格都叫一“步”），每走一步人数就减半，因此A处有
3×2×2×2×2×2×2＝192（人）
根据A处的人数，不难求出D、E、F处各走过96，48，24人，H、G处各走过96，72人，由此可知走过C的人数为48（人）。
[解]
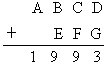
可以看出A=1。
因为不同字母表示不同的数，所以D＋G≠3，（否则D、G中就要有1），只能是D＋G=13。
因为C＋F≠18，C＋F＋1的个位是9，所以C＋F＝8。
这时B＋E=9
由C＋F=8知，C、F同为奇数或同为偶数，如果C，F中一个是2，另一个是6，那么在3，4，5，7，8，9中找不到四个不同数B，D，E，G，使B+E=9，D＋G=13，如果C，F中一个是3，另一个是5，那么D、G中一个是4，另一个是9，B、E中一个是2，另一个是7。
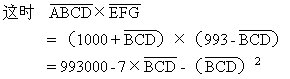
乘积的最大值是993000－7×234-2342=936606，乘积的最大值是993000-7×759-7592=411606，最大值与最小值的差是936606-411606=525000。
[分析与讨论]这是一个算式中的整数分析问题，要求解题者能列出
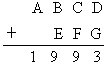
行字母可取值的分析。自已列算式，再根据算式进行分析要比给你一个算式，让你进行分析要求高些。
有的同学随便凑了几个数，就算出了最大值，最小值，这种做法是不够好的。我们提倡在分析的基础上得出结论，而不是猜与凑。
（5）一组互不相同的自然数，其中最小的数是1，最大的数是25，除1之外，这组数中的任一个数或者等于这组数中某一个数的2倍，或者等于这组数中某两个数之和，问：这组数之和最大值是多少？当这组数之和有最小值时，这组数都有哪些数？并说明和是最小值的理由。
[解]数组1，2，3，4，5，…，25的和最大，它们的和是
1+2＋3＋…+25＝325
下面考虑数组中各数之和最小时的情形。
由小到大排出这组数，可能是
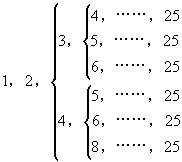
25只能是比它小的另外两个不同数之和，在上面六种可能性中，没写出来的数（用虚线表示）中，至少要有两个数，它们的和不小于25，不然的话，最后的25就表不成组中某两数之和，为使数组中各数之和尽量小，应当在“…”处填入尽量少的数，并使后填入的数之和尽量小。
在1，2，3，4，…，25中，“…”处不能只填5，20；6，19；7，18：8，17；9，16；10，15；11，14；12，13。也就是说，不时能在“…”处只填入两个数，使这两个数之和是25。
在1，2，3，5，…，25中的“…”处，可以只填10，15两个数，可见数组1，2，3，5，10，15，25的和最小，最小的和是1＋2＋3＋5＋10＋15＋25＝61。
[讨论]这是整数分析类的题目，我们实际上做了两件事：
①1，2，3，5，…，25中的虚线处，可以填入和为25的两个数10，15，这个数组的和是61。
②说明了任何其他数组的和不比61小，根据这两点，就可以断定最小的和是61。
（6）一条大河有A、B两个港口，水由A流向B，水流速度是4公里/小时。甲、乙两船同时由A向B行驶，各自不停地在A、B之间往返航行，甲在静水中的速度是28公里/小时，乙在静水中速度是20公里/小时，已知两船第二次迎面相遇地点与甲船第二次追上乙船（不算开始时甲、乙在A处的那一次）的地点相距40公里，求A、B两港口的距离。
[解法1]设A、B两个港口相距S公里，甲、乙两船第二次迎面相遇时的位置与港口B相距X公里，甲船第二次追上乙船时的位置与港口B相距Y公里。
第一步先求X。因为甲、乙船同时从港口A开始航行，在第二次迎面相遇时，它们共航行了4S公里。甲船逆水速度是24公里/小时，乙船顺水速度也是24公里/小时。从这个条件，我们可以判断甲船航程在2S公里和3S公里之间，其中逆水航程为S公里，乙船航程在S公里和2S公里之间，其中顺水航程为S公里。（想想为什么？）因此甲船逆水航行时间和乙船顺水航行时间相同，甲顺水航行时间和乙逆水航行时间相同，并且共计航行2S公里。所以
第二步求Y。甲船第二次追上乙船时，甲船比乙船多航行了4S公里，其中顺水是2S公里，逆水是2S公里。先假设甲船在逆水航行时追上乙船，并且在追上乙船时，乙船顺水航行了nS公里，逆水则航行了nS-S+Y公里。这时可以列出算式：（为什么？）
2Y＝（16-3n）S。
[解法2]设A、B两个港口的距离为总体1。由题目所给条件可以得到：
甲船顺水速度：乙船顺水速度=4∶3，
甲船逆水速度：乙船顺水速度=1∶1，
甲船顺水速度：乙船逆水速度=2∶1，
甲船逆水速度：乙船逆水速度=3∶2。从这些速度比，可以很快计算出
这些速度比，可以计算在某同一时刻时甲、乙两船所在的位置。
上面的图表中，箭头→表示顺水航行，←表示逆水航行。0表示船在港口A，1表示船在港口B，分数表示船距港口A的位置。在同一竖直方向上两个箭头方向相反时，甲、乙船必定会迎面相遇。所以，从上面的图表自左向右一组一组地观察两个箭头的方向，可以发现，第二组两个箭头第一次方向相反。而第四组两个箭头第二次方面相反。甲、乙两船会第二次相遇，此时，它们距港口A等于
若在同一竖直方向上两个箭头方向相同，并且 甲船的位置在乙船行驶方向的后方变为在乙船的前方或位置相同时，则表示在这一段行驶时甲船追上了乙船。例如自左向右第七组两箭头方向相同，都是逆水航行，在这一段航行时，
察，可以得到，甲第二次追上乙船时，它们距港口A等于
（想想为什么？）所以A、B两港口相距
[说明与讨论]
（1）在解法1的第二步中，我们假定甲船在逆水航行时追上乙船，并
行的情况下第二次追上乙船了。道理是很简单的：我们解一道数学题时，这道题或者没有解，或者有唯一的一个解，或者有几个甚至无穷多个解。如果题目只有唯一的一个解答，我们求出这个解答之后，对于其他情况，或者题目没有解，或者解答和已经得到的解答相同。所以就不需要再考虑其他情况了。在这道行程问题中，甲船能够第二次追上乙船，追上时的位置当然只有
船顺水航行是否会第二次追上乙船了。实际上，同学们可以试算一下，这时，Y不可能有合理的解答。
（2）这是一道相遇，追击和带有逆水行程的混合行程问题。行程问题是小学高年级和初中一年级应用题中很重要的类型。而解行程问题的关键是清楚地理解时间，行程和速度这三个量之间的关系，在解法1中，关键是理解甲、乙两船的行程和时间关系，在解法Ⅱ中，关键是理解甲、乙两船的速度关系，计算过程步骤略多一些，需要同学们具有准确和快速的运算能力。这道行程问题还有其它解法，只要同学们能准确地理解时间，速度，距离这三个量之间的关系，相信同学们能给出更简单的解答方法来。
决赛第二试
（1）互为反序的两个自然数的积是92565，求这两个互为反序的自然数。
（例如102和201；35和53，11和11，…称为互为反序的数，但120和21不是互为反序的数）
[解法1]分解因子 92565=3×3×5×11×11×17互为反序的两个自然数中，若其中之一为3的倍数（或11的倍数），另一个也必为3的倍数（或11的倍数），又因乘积是五位数，所以这两个数是三位数，我们有
92565＝（3×5×11）×（3×17×11）
＝165×561
[答]这两个数为165和651。
[解法2]因为积是五位数，这两个数都是三位数。积的个位数是5，因此其中第一个乘数的个位数也必是5，经反序后，第二个乘数的百位数为5。第一个乘数的百位数若不小于2，则积必为六位以上的数，因此，第一个乘数百位数是1，第二个乘数的个位数是1，这样一来，这两个反序数一定形
是3，6，9，0中之一，计算得
531×135=71685
561×165=92565
591×195＝115215
501×105＝52605
[分析与讨论]解法1中利用了两个整除性判断准则；（1）一个自然数的各位数字之和为3的倍数，则这个自然数是3的倍数，反之亦然；（2）一个自然数奇位数字之和与偶位数字之和的差是11的倍数，则这个自然数是11的倍数。反之亦然。互为反序的两个自然数，它们各位数字之和是相同的；且奇位数字之和与偶位数字之和的差也是不变的。因此，它们同为3和11的倍数。将92565分解因子之后，就很容易定出这两个数来。
有利用3的整除性准则。而是用试算法，但他并不从1-9逐个数进行试算，
面对于比5小的数就不算了，而只在5-9之间找一数进行试算，直到确定
（2）某工厂的一个生产小组，生产一批零件，当每个工人在自己原岗位工作时，9小时可完成这项生产任务。如果交换工人A和B的工作岗位，其它工人生产效率不变时，可提前一小时完成这项生产任务；如果交换工人C和D的工作岗位，其它工人生产效率不变时，也可以提前一小时完成这项生产任务。问： 如果同时交换A与B，C与D的工作岗位，其它工人生产效率不变，可以提前几分割完成这项生产任务？
效不变，所以这一份就是 A、B二人多干的。
同理，C与D交换后，他们二人每小时也要多干1份任务。
同时交换后，A与B，C与D每小时都多干一份任务，所以全组工人每
每干1份任务，提前7.5-6=1.5分钟，72份任务一共提前72×1.5＝108分钟。
［答］可提前108分钟。
［解法2］i）设总工作量为1，则原来全组每小时完成1/9。
iii）C与 D交换后，他们二人每小时也多干
[解法3]A与B交换后，全组在8小时内完成原来9小时的工作，由于其它人工效不变，所以A、B二人在8小时中多干了原来全组人1小时的工作。
同理C与D交换后，他们二人在8小时中多干了原来全组人的一小时工作。
A与B，C与D同时交换后，他们四人就在4小时内多干了原来全组人1小时的工作。这就是说，A与B，C与D同时交换后，全组人工在4小时内干了原来全组人在5小时内干的工作，即缩短工时1/5。
[分析与讨论]工作效率问题是小学四则运算的典型应用问题之一，但实际的生产计划要复杂得多，这是因为生产链中某一环节的效率发生变化后，其它的环节的效率也相应地发生改变，利用数学方法安排生产计划是一门专门学科，是管理科学和运筹学的研究内容，在我们的问题中，强调A与B（或C与D）交换工作岗位后，其它工人的生产效率不变，就是说交换岗位的工人们是俩俩互相影响对方的工作效率，而对其它工人的效率不发生影响。如果不是这样，那么就需要更多的已知条件，应用更为复杂的数学方法将实际问题变成一个数学问题，是一个抽象与简化的过程，同一实际问题有着不同的方法将其抽象简化成不同的数学问题，即便是最为通常的植树问题也是这样，因为要植树，就得有挖坑、裁苗、浇水等工序，这些工序各有各的工效，互相影响。若要仔细研究，则必需运用运筹学方法。
（3）某校学生中，没有一个学生读过学校图书馆的所有图书，又知道图书馆内任何两本书至少被一个同学都读过，问：能不能找到两个学生甲、乙和三本书A、B、C，甲读过A、B，没读过C，乙读过B、C，没读过A？说明判断过程。
[解法1]首先从读书数最多的学生中找一人叫他为甲，由题设，甲至少有一本书C未读过，
设B 是甲读过的书中的一本，根据题设，可找到学生乙，乙读过B、C。
由于甲是读书数最多的学生之一，乙读书数不能超过甲的读书数，而乙读过C书，甲未读过C书，所以甲一定读过一本书A，乙没读过A书，否则乙就比甲至少多读过一本书，这样一来，甲读过A、B，未读过C；乙读过B、C未读过A。
因此可以找到满足要求的两个学生。
[解法2]将全体同学分成两组。
若某丙学生所读的所有的书，都被另一同学全部读过，而后一同学读过的书中，至少有一本书，丙未读过，则丙同学就分在第一组。另外，凡一本书也未读过的同学也分在第一组，其余的同学就分在第二组。
按照以上分组方法，不可能将全体同学都分在第一组，因为读书数最多的同学一定在第二组。
在第二组中，任找一位同学叫做甲，由题设有书C，甲未读过。再从甲读过的书中任找一本书叫做B，由题设，可找到同学乙，乙读过B、C书，由于甲属于第二组，所以甲一定读过一本书A，乙未读过A，否则甲只能分在第一组，这样，甲读过A、B，未读过C；乙读过B、C，未读过A。
[分析与讨论]这是一个逻辑推理题，目的是考察同学们的推理能力，促进同学们加强逻辑推理能力的训练。解法1中从一个读书数最多的同学出发，也就是从具有某种特殊性的对象着手，这一方法是推理中常用到的，有些人称为“极端原则”。开始利用这一原则试一试，可以解决我们“无从着手”的难处，解法2中将同学们分成两组，但重要的一步是要说明第二组中一定有同学，正确地分组是解决这一问题的关键。
（4）有6个棱长分别是3cm，4cm，5cm，的相同的长方体，把它们的某些面染上红色，使得有的长方体只有一个面是红色的，有的长方体恰有两个面是红色的，有的长方体恰有三个面是红色的，有的长方体恰有四个面是红色的，有的长方体恰有五个面是红色的，还有一个长方体六个面都是红色的，染色后把所有的长方体分割成棱长为1cm的小正方体，分割完毕后，恰有一面是红色的小正方体最多有几个？
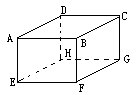
[解]如上图，AD＝BC=EH=FG=5cm
AB＝CD＝EF＝GH＝4cm
AE＝BF＝CG＝DH＝3cm
i）一面染色，将ABCD染红，则有20个一面是红色的小立方体，而染其它面不能得到多于20个一面是红的小立方体。
ii）二面染色，将ABCD和EFGH染红色的，则可得到40个一面为红色的小立方体，将其它二面染红色的，不能得到多于40个一面为红色的小立方体。
iii）三面染色，将ABCD，EFGH和ABEF染红色，将得到36个一面为红色的小立方体。将其它三面染色，将不可能得到多于36个一面为红色的小立方体。
iv）四面染色，将ABCD，EFGH，ABFE和CDHG染红色，将得到32个一面为红色的小立方体，这是最多的可能。
v）五面染色，将ABCD、EFGH，ABFE、CDHG和CBFG染红色，将得到27个一面为红色的小立方体，这是最多的可能。
vi）六面染色，可得22个一面染色的小立方体。
22＋27＋32＋36＋40＋20=177
[答]最多可得到177个一面为红色的小立方体。
[分析与讨论]这一题的难点在于“最多有几个？”，在三面染色的情况，染两个最大面，再染一个次大面，则可得到35个有一面为红色的小立方体；而染两个最大面，再染一个最小面则可得到36个有一面为红色的小立方体，这是因为3.4.5这三个数的特殊性。如果边长不是3、4、5，而是l、m、n三个自然数，且l、m、n三个数中最小的也比3大，则情况就不一样了，得到正确答案的同学可能就会多一些。具体问题应该具体分析，不能一概套用成法。
（5）小华玩某种游戏，每局可随意玩若干次，每次得分是8，a（自然数），0这三个数中的一个，每局各次得分的总和叫做这一局的总积分，小华曾得到过这样的总积分：103，104，105，106，107，108，109，110，又知道他不可能得到“83分”这个总积分。问：a是多少？
[解法1]由于103到110相继八个自然数都是可得分数，所以不小于103的任何自然数都是可得分数。
由于103是奇数，所以a必为奇数，或（a，8）＝1（（a，8）表示a与8的最大公约数）。
i）确定a的下界。考察八个数：
0，a，2a，3a，4a，5a，6a，7a，（＊）
是说，（＊）中的八个数除8后，有8个不同的余数：0，1，2，3，4，5，6，7。
对于任何一个大于7a的自然数N，N除以8后的余数，必为0，1，2，
7），使得N-na=8的倍数=8m＞0，
因此 N=na＋8m
而N是可得分数，7a当然是可得分数，所以83必小于7a，即83＜7a，
ii）确定a的上界
若自然数7a-8是可得分数，则有
7a-8＝8p＋qa
p、q为自然数或0，
（7-q）a=8（p+1）＞0
这就是说8｜（7-q）a，而（8，a）＝1，所以8｜（7-q）而7＞7-q＞0因此，这是不可能的，我们得到7a-8是不可得分数。由于不小于103的自然数都是可得分数，所以，7a-8＜103，即
iii）确定a
由i）和iii）得到，11＜a＜16，且a为奇数，所以a只可能是13或15，又因
83＝8+5×15
所以a≠15，下面检验a=13是否满足题意，
由i）知道，大于7×13＝91的自然数都是可得分数，所以103到110都是可得分数，另外
83-13=70不是8的倍数
83-3×13=44不是8的倍数
83-5×13＝18不是8的倍数
所以83是不可得分数，a＝13，满足题意，
[答]a＝13。
[解法2]
i）由于103是奇数，所以a一定是奇数。
ii）从题设条件中，我们知道83是不可能得到的总积分，当n为不大于10的任一自然数时，83-8n不能有的数a，否则83=8n+ma为可得分数，因此。
83-8×10=3所以a≠3
83-8×9=11所以a≠11
83-8×8＝19所以a≠19
83-8×7＝27＝3×9所以a≠9
83-8×6=35=5×7所以a≠5，a≠7
83-8×5＝43所以a≠43
83-8×4=51=3×17所以a≠17
83-8×3＝59所以a≠59
83-8×2=67所以a≠67
83-8＝75=3×5×5所以a≠15，a≠25
综上所述a是大于11的奇数，且不能是15，17，19，43，59，67，
iii）检验a=13是否满足题意。
由ii）可知，当a=13时，83是不可能得到的总积分。而
103＝8×8＋3×13
104＝8×13
105＝8×5＋5×13
106＝8×10+2×13
107＝8×2＋7×13
108＝8×7＋4×13
109=8×12+13
110=8×4+6×13
满足题意，因此a=13是问题的解。
iv）说明a=13是问题的唯一解，大于13的奇数还有很多，我们不能逐一地去检验。因此，我们还要说明a的上界。
从103到110八个总积分都是自然数，它们除8后的余数分别是，7，0，1，2，3，4，5，6因为7a不能被8整除，7a除8后的余数必是1，
到110中找到一个数N使得N除8后的余数与7a除8后的余数相同所以
7a-N=8的倍数=8m＞0
而N是可得到的总积分数，即
N＝pa＋8q，p，q为自然数或0
所以（7-p）a=8（m＋q）＞0
7＞7-q＞0
这表明8｜（7-q）a，而（8，a）=1，所以8｜（7-p）
都不能是问题的解。
[分析与讨论]这一题主要是检查同学们整除性的理解程度及培养同学们的严密逻辑思维方法，有的同学从1开始逐个奇数试算得到13，但这并不能说明只有13这一个解，因为并没有说明大于13的奇数一定不是问题的解。
在数学问题中，有许多问题是暂时不可能精确地确定某个量的大小的；或不需要知道它的精确大小，而能够知道它的上、下界就足够了，学会从已知条件出发，给出某个量的界的分析方法对于求解许多数学问题都是十分重要的。
另外，我们考虑下面问题：用8分和13分的邮票，可以支付哪些不同的邮资？大家一定看得出来，我们的试题（5），是“邮资”问题的“反问题”。实际上，在我们学习数学课程中，已经遇到过许多的问题和它们的反问题，同学们可以试一试，从自己做过的习题中，找来几个问题，提出它们相应的反问题做一做。
（6）在正方体的8个顶点处分别标上1，2，3，4，5，6，7，8，然后再把每条棱两端所标的两个数之和写在这条棱的中点，问各棱中点所写的数是否可能恰有五种不同数值？各棱中点所写的数是否可能恰有四种不同数值？如果可能，对照图a在图b的表中填上正确的数字；如果不可能，说明理由。
[解法1] i）各棱中点处所写的数恰有五种不同数值是可能的，但填法不唯一。
ii）不可能少于五种不同数值。
以1所在顶点为端的棱有三条，不妨设这三条棱的另一端点所填写的数是a、b，c，满足a＜b＜c，则这三条棱的中点处的数为1＋a，1+b和1＋c，满足1+a＜1+b＜1+c。
以8所在顶点为端点的棱也有三条，设这三条棱另一端点所填写的数为x、y、z，满足x＜y＜z，则这三条棱的中点处的数为8＋x，8＋y，8＋z，满足8＋x＜8＋y＜8＋z。
只有当c=8，x＝1时，以上六条棱中点处的数才能恰有五个不同的数值，否则就多于五种不同数值。而这六条棱中点的六个数不可能少于五种不同的值，因此在12条棱的中点处所写的数不可能有少于五种不同的数值。
[解法2]i）各棱中点处所写的数恰有五种不同的数值是可能的（见解法1）
ii）各棱中点处所写的数恰有四种不同的值是不可能的，以下说明理由。
首先给出在任一确定的填写法中，写在顶点的数与写在中点的数的关系及特征：
（1）每一写在中点的数有两个加项，它们都是写在顶点的数（题设），若α＝a＋b，则称“写在顶点的数a（或b）为写在中点的数α的组成”。
（2）每一写在顶点的数（1，2，…，8）恰为三个写在中点的数的组成，不能多，也不能少。这是因为立方体的每一顶点恰是三条梭的端点，因此，12个写在中点的数之和等于8个写在顶点的数之和的3倍，即108。
（3）写在中点的数的可能值，该写在中点的数的可能组成及该写在中点的数最多可能占有的棱的条数满足下表1所示的关系。
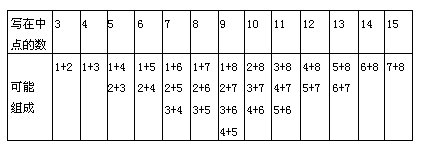
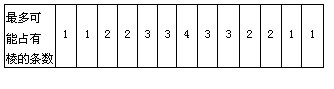
如果恰有四种不同的值是可能的，我们可以设这四个数是a，b，c，d。
若这四个数中，有一个只写在一条棱上，则必有另两个数都写在四条棱上，或另一个数写在五条棱上，由表1可以看出这是不可能的。
若有一数，不妨设是a，只写在两条棱上（或称为占有两条梭），则必有一数写在四条棱上，设它为b。由表1可知b＝9。由特征（2）
2a＋3（c＋d）=108-36=72
可见，a是3的倍数，即a=6或12（3和15不可能写在两条棱上）。当a=6时。
c＋d＝20
写在3条棱上。
当a=12时，c+d=16
综上所述，a，b，c，d四个数中不可能有一个数只写在两条棱上，也不可能写在一条棱上，也不可能写在四条以上的棱上（因为一共只有12条棱）因此， a，b，c，d每个数只能都写在三条棱上，由特征是
3×（a＋b＋c+d）=108
a＋b+c+d=36
由表1可知，a，b，c，d只能是7，8，9，10，11这五个数中的四个，这是因为其它的数部不可能写在三条棱上，而，
7＋8＋9＋10 ＋11-（a＋b＋c+d）
=45-36=9
所以a，b，C，d恰是7，8，10，11这四个数，当这四个数都写在三条棱上时，数6必须同时是这四个数的组成（见表1），这与特征（2）不符。所以，不可能恰有四个值。
[分析与讨沦]解法1巧妙而简洁，它不仅证明了取四个值是不可能的，而且标出，要恰取五个值，就必须将1和8这两个数写在一条棱的两个端点上，这一方法的关键在于抓住了通过1和8所在顶点的六条棱。
解法2是反证法，它虽然显得有些繁琐，但却给出了更多的信息，尽管有解法1可用，而不需要这许多信息，但是在求解其它有关问题时，就可能用到。例如问：是否有可能12条梭上所写的数恰有12个不同的值？同学们可以做一做。
团体决赛口试
（1）2×3×5×7×11×13×17
这个算式中有七个数连乘
请回答：最后得到的乘积中，所有数位上的数字和是多少？请讲一讲你是怎样算的？
[答]最后得到的乘积中，所有数位上的数字和是12。
[理由]2×3×5×7×11×13×17
＝（2×5）×（7×11×13）×（3×17）
=10×1001×51
=10010×51
＝510510
510510所有数位上的数字之和是
5＋1＋0＋5＋0＝12
[说明]本题考察应用乘法运算律进行速算巧算的技巧，其中熟悉7×11×13＝1001这个事实会使心算速度更快一些。
（2）这是一个中国象棋盘（图中小方格都是相等的正方形，“界河”的宽等于小正方形边长），黑方有一个“象”，它只能在1，2，3，4，5，6，7位置中的一个，红方有两个“相”，它们只能在8，9，10，11，12， 13，14中的两个位置。
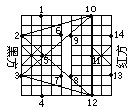
问：这三个棋子（一个“象”和两个“相”）各在什么位置时，以这三个棋子为顶点构成的三角形的面积最大？
[答]黑象在2或3的位置，两个红相分别在10，12的位置时，以这三个棋子为顶点的三角形（2，10，12）或（3，10， 12）的面积最大（如图所示）。
[理由]我们设每个小方格的边长为1单位，则，小方格正方形面积为1平方单位。
由于三个顶点都在长方形边长的三角形面积至多为这个长方形面积的一半，所以要比较这些三角形面积寻求最大者，只要比较它们顶点所在边构成的长方形面积寻找最大者就可以了。
直观可见，只须比较（3，10，12）或，（2，10，12）与（3，10，13）或（2，12，14）这两类三角形面积就可以了。
顶点为（3，10，12）或（2，10，12）的三角形面积为
顶点为（3，10，13）或（2，12，14）的三角形面积小于
所以顶点在（2，10，12）或（3，10，12）时三角形面积最大。
（3）
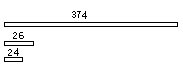
将一根长为374厘米的合金铝管截成若干根36厘米和24厘米两种型号的短管（加工损耗忽略不计）
问：剩余部分的管子最少是多少厘米？
[答]剩余部分的管材最少是2厘米。
[理由]24厘米与36厘米都是4的倍数，所以截成若干根上述两种型号的短管用料总长度必是4的倍数，但374被4除余2，所以截完以后必有剩余，剩余管料长不小于2厘米。
另外，24＋36=60（厘米），截五次共用料300厘米，再截两根36厘米短管，用料72厘米，恰剩2厘米管料。即
因此剩余部分的管子最少是2厘米。
(4)
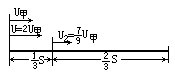
人谁先到达B？请你说明理由。
[答]甲先到达B。
所以乙比甲后到达B点，即甲先到达B。
[说明]本题也可采用如下解法。
时间相同。
所以甲先到达B
（5）这是一个长方形。
（AE的长度与ED的长度之比是9∶5）
（BF的长度与FC的长度之比是7∶4）
问：涂红色的两块图形的面积与涂蓝色的两块图形的面积相比较，哪个大？请说明理由。
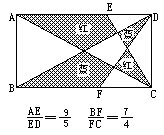
[答]涂红色两块图形的面积大。
所以 AE＞BF
但△ACE与△BDF高相等（都是CD），
所以△ACE面积＞△BDF面积。
减去中间空白的小四边形面积，得
涂红色的两块图形的面积大于涂蓝色的两块图形的面积。
（6）这是一个正方形，图中
所标数字的单位是厘米。
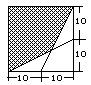
问：涂红色的部分的面积是多少平方厘米？
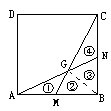
[理由]容易发现，M是AB中点、N是BC中点、连BG，形成四个小三角形，我们依次记成△①，△②，△③，△④如图所示。
容易计算
△ABN与△CBM的面积相等，都等于正方形ABCD面
△①的面积=△④的面积。
又根据等底等高的两个三角形面积相等，有
△①的面积△②的面积。
△③的面积=△④的面积
所以△①的面积=△②的面积=△③的面积=△④的面积。
因此△①，△②，△③，△④面积总和为
由于正方形边长为20厘米，面积为400平方厘米。
所以涂红色部分的面积为
[说明]本题还可采用如下解法。如图，连AC、GB。
易知M为AB中点，N为BC中点。
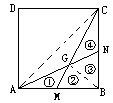
△ABC面积为
△BDC面积也为200平方厘米。
由等底等高三角形面积相等，可知
△ACM面积=△BCM面积，……①
△AGM面积=△BGM面积，……②
①-②得△ACG面积=△BCG面积……③
同理可得
△CAN面积=△BAN面积……④
△CGN面积=△BGN面积……⑤
④-⑤得△CAG面积=△BAG面积……⑥
由③与⑥得
△ACG面积=△BCG面积=△BAG面积
因此 四边形DAGC的面积
=△ACD面积+△ACG面积
（7）
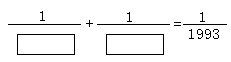
这是两个分数相加的算式。
问：等号左边的两个方格中各是怎样两个不同的自然数？
[答]一个方格填1994，另一个方格填
1993×1994＝这两个自然数，使得
比较得 R=1994
1993R＝1993×1994＝。
于是得
〔说明〕作为一般情况，有关系式
其中n是自然数。
本题中先取2n＋1＝1993，
解得 n＝996，所以n＋1=997。
（n+1）（2n+1）＝997×1993＝
所以有
（8）在三位数中，数字和是5的倍数的数共有多少个？
[答]在三位数中，数字和是5的倍数的数共有180个。
[理由]如下十个连续的三位数
称为一个三位数“数段”，它们每个的数字和也恰依次排列为十个连续的自然数：
a1＋a2＋0，a1＋a2＋1，a1＋a2＋2，……，a1＋a2+9
其中有且只有两个是5的倍数。
从100-999共有900个三位数，可分成如上所述的90个三位数“数段”：
100，101，102，103，104，105，106，107，108，109；
110，111，112，113，114，115，116，117，118，119；
……
990，991，992，993，994，995，996，997，998，999。
由于每个三位数“数段”中有且只有两个数数字和为5的倍数。所以，总计在三位数中，数字和是5的倍数的数共有
2×90=180个
（9）图中有两个红色的正方形，两个蓝色的正方形，它们的面积已在图中标出（单位：厘米2）
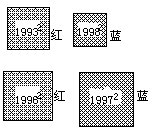
问：红色的两个正方形面积大还是蓝色的两个正方形面积大？请说明理由。
〔答〕蓝色的两个正方形的面积大。
〔理由〕将蓝色小正方形放入红色小正方形中，如图看出19932比19922大
2×1992+1
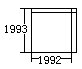
将红色大正方形放入蓝色大正方形中，如图看出19962比19972小
2×1996+1
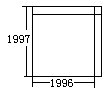
由于2×1992＋1＜2×1996＋1
因此，两个红色正方形面积的总和要比两个蓝色正方形面积总和小。
即两个蓝色正方形的面积大。
（10）
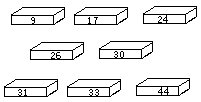
八个盒子，各盒内装奶糖分别为9，17，24，28， 30，31，33，44块。
甲先取走了一盒，其余各盒被乙、丙、丁三人所取走。已知乙、丙取到的糖的块数相同且为丁的两倍。
问：甲取走的一盒中有多少块奶糖？
〔答〕甲取走的一盒中有31块奶糖。
[理由]由已知，乙、丙、取到糖块数之和为丁的4倍，乙、丙、丁三人取走的七盒中糖的块数是丁所取糖块数的5倍。即乙、丙、丁三人取走的七盒中糖的块数是5的倍数。
而八盒糖的总块数是
9＋17＋24＋28＋30＋31＋33＋44=216
而从216减去5的倍数所得差的个位数字只能是1或6。
观察各盒糖的块数发现，没有各位数字是6的数，只有31一个个位数字是1的数。因此，判定中甲取走的一盒中有31块奶糖。
（11） 这是一块正方形的地板砖示意图。其中
AA1＝AA2＝BB1=BB2=CC1＝CC2＝DD1＝DD2
红色小正方形的面积是4，绿
色的四块面积总和是18。
求 这个大正方形ABCD的面积，请说明理由。
[答]大正方形ABCD的面积是50。
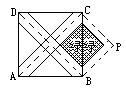
[理由]如右图连AC、BD、交于O点。将△AOD割下补到△BPC的位置。
3。红色正方形被分成四个面积为1的小正方形，所以正方形OBPC的白色边缘厚度为1。因此，正方形OBPC的边长OC=5，面积为25。这个面积恰是正方形ABCD面积的一半，所以正方形ABCD的面积是50。
（12） 这是一个围棋盘，还有一堆围棋子，将这堆棋子往棋盘上放，当按格点摆成某个正方阵时，尚多余12枚棋子，如果要将这个正方阵改摆成每边各加一枚棋子的正方阵，则差9枚棋子才能摆满。
问：这堆棋子原有多少枚？
［答］这堆棋子原有112枚。
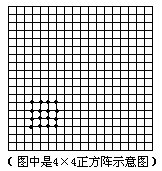
[理由]第一次排方阵剩余12枚，加上第二次排方阵所不足的4枚，恰是原正方阵扩大后“贴边”的部分（如图所示），共21枚，它恰是原正 方阵每边棋子数与“扩阵”每边棋子数之和。它们恰是两个相邻的自然数之和，所以原正方形阵每边10枚棋子、新正方阵每边11枚棋子。这堆棋子总数是
102＋12=112枚。
〔说明〕本题也可列方程求解
设原正方阵每边m枚棋子，由题意得
（m＋1）2-9＝m2＋12
即 2m＋1=21
解得 m=10
所以棋子总数为102＋12=112枚。
（13）如图是一个古座钟的图面，问：红色部分面积与蓝色扇形的面积之间大小关系如何？
请说明理由。
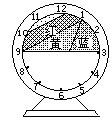
[答] 红色部分面积与蓝色扇形的面积一样大。
相等△AOE面积=△EOB面积。
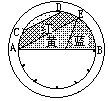
所以图中黄色部分面积等于扇形OBE的面积。
因此，红色部分面积也恰等于一个扇形OBE的面积。所以，
红色部分面积与蓝色扇形的面积一样大。