1,如图,把左边的图形折叠起来,它会变为 ( )
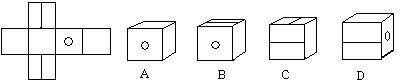
2,下面图形经过折叠不能围成棱柱的是 ( )
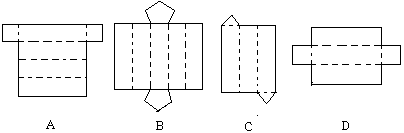
3,如图,把左边的图形折叠起来,它会变成 ( )
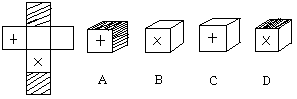
4,一个几何体的边面全部展开后铺在平面上,不可能是 ( )
A.一个三角形 B.一个圆 C.三个正方形 D.一个小圆和半个大圆
5,(1)侧面可以展开成一长方形的几何体有 ;
(2)圆锥的侧面展开后是一个 ;
(3)各个面都是长方形的几何体是 ;
(4)棱柱两底面的形状 ,大小 ,所有侧棱长都 .
6,用一个边长为4cm的正方形折叠围成一个四棱柱的侧面,若该四棱柱的底面是一个正方形,则此正方形边长为 cm.
7,用一个边长为10cm的正方形围成一个圆柱的侧面(接缝略去不计),求该圆柱的体积.
8,用如图所示的长31.4cm,宽5cm的长方形,围成一个圆柱体,求需加上的两个底面圆的面积是多少平方厘米?(![]() 取3.14)
取3.14)
![]()
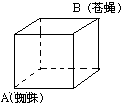
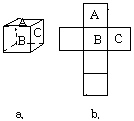
1,如图,在一个正方体木块的两个相距最远的顶点外逗留着1只苍蝇和1只蜘蛛,蜘蛛沿哪条路径去捉苍蝇最快?请说明理由.
第9题图 第10题图
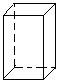
2,如图,正方体a的上、前、右三个面上分别注有A,B,C三个字母,它的展开图如图b所示,请用D,E,F三个字母在展开图上分别标注下、后、左三个面.
 3,如图,一个长方体的底面是边长为1cm的正方形,侧棱长为2cm,现沿图中粗黑线的棱剪开,请画出展开图。
3,如图,一个长方体的底面是边长为1cm的正方形,侧棱长为2cm,现沿图中粗黑线的棱剪开,请画出展开图。
4,已知圆锥的侧面展开图是一个半圆,求它的侧面积与底面积的比.
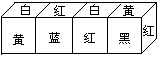
1,在正方体的六个面上分别涂上红、黄、蓝、白、黑、绿六种颜色,现有涂色方式完全相同的四个正方体,如图拼成一个长方体,请判断涂红、黄、白三种颜色的对面分别涂着哪一种颜色?
2,如图,已知一个正方体的六个面上分别写着
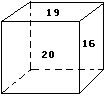 六个连续的整数,且每两个相对面上的两个数的
六个连续的整数,且每两个相对面上的两个数的
和都相等,图中所能看到的数是16,19和20,
求这6个整数的和.
3,如图所示的积木是由16块棱长为1cm的正方体堆积而成的,请求出它们的表面积.
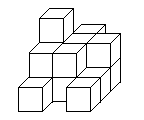
4,用小立方块搭一几何体,使它的主视图和俯视图如图所示,俯视图中小正方形中的字母表示在该位置小立方块的个数,请问:
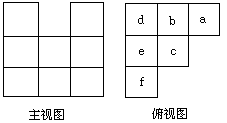
(1)a,b,c各表示几?
(2)这个几何体最少由几个小正方块搭成?最多呢?
(3)当d=e=1,f=2时,画出这个几何体的左视图.
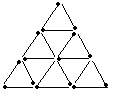
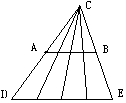 1.如图,图中三角形的个数为( )
1.如图,图中三角形的个数为( )
 A, 2 B,
18 C, 19 D, 20
A, 2 B,
18 C, 19 D, 20
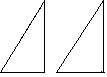
2.将两个完全相同的三角形,如图,拼在一起成为四边形,使它们有一条线等的边完全重合,则能拼出不同的平面图形( )种
 A, 2 B, 4 C, 6 D, 8
A, 2 B, 4 C, 6 D, 8
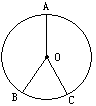
3. 如图,如果OA,OB,OC是圆的三条半径,那么图中有 个扇形.
4.如果从一个多边形的一个顶点出发,分别连接这个定点与其余各顶点,可将这个多边形分割成2003个三角形,那么此多边形的边数为
5(1)若将n边形内部任意取一点P,将P与各顶点连接起来,则可将多边形分割成 个三角形.
 (2)若点P取载多边形的一条边上(不是顶点),在将P与n边形各顶点连接起来,则可将多边形分割成 个三角形.
(2)若点P取载多边形的一条边上(不是顶点),在将P与n边形各顶点连接起来,则可将多边形分割成 个三角形.
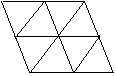
6.如图,图中共有 个梯形。
7,平面内有5个点,每两个点都用直线连接起来,则最多可得 条直线,最少可得 条直线。
8.平面内三条直线把平面分割成最少 块最多 块。
9.已知扇形弧上连同两个端点共有4个点,将这4点与圆心连接,则共可得 个扇形。
10.已知圆上有5个点,这5个点把这个圆周共分成多少条不同的弧?
 11.平面内有10条直线,它们可以有多少个交点。
11.平面内有10条直线,它们可以有多少个交点。
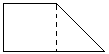
12.请将下图的图形分成四个形状相同、大小相等的图形。
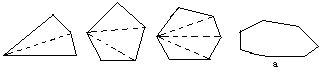
13。每一个多边形都可以按下图的方法分割成若干个三角形。那么用同样的方法,图a中的七边形能分割成若几个三角形?n边形又能分割成若几个三角形?
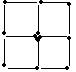
14 (1)移动四根火柴,组成三个全等的正方形。
(2)移走3根火柴,组成6个全等的等边三角形。
1、面与面相交成___,线与线相交得到___,点动成____,线动成_____,面动成____
2、下面是两种立体图形的展开图.请分别写出这两个立体图形的名称:________,___________
 3、下图所示的三个几何体的截面分别是:(1)_________;(2)__________;(3)___________.
3、下图所示的三个几何体的截面分别是:(1)_________;(2)__________;(3)___________.

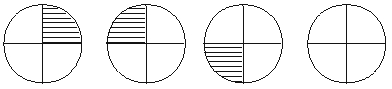
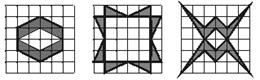
4、图中按左侧三个图形阴影部分的特点,将右侧的图形补充完整.
 |
5、已知三棱柱有5个面、6个顶点、9条棱,四棱柱有6个面、8个顶点、
12条棱,五棱柱有7个面、10个顶点、15条棱,……,由此可以推测n棱
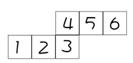 柱有_____个面,____个顶点,_____条棱。
柱有_____个面,____个顶点,_____条棱。
6、当下面这个图案被折起来组成一个正方体,数字_______会在
与数字2所在的平面相对的平面上
7、从一个多边形的某个顶点出发,分别连接这个点和其余各顶点,可以把这个多边形分割成10个三角形,则这个多边形的边数为_____。
8、已知一不透明的正方体的六个面上分别写着1至
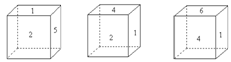 6六个数字,如图是我们能看到的三种情况,那么
6六个数字,如图是我们能看到的三种情况,那么
1和5的对面数字分别是____和_____。
9、下面几何体的截面图不可能是圆的是 ( )
A、圆柱 B、圆锥 C、球 D、棱柱
10、将左边的正方体展开能得到的图形是 ( )
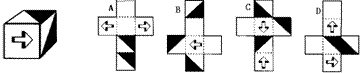
11、将半圆绕它的直径旋转一周形成的几何体是 ( )
A、圆柱 B、圆锥 C、球 D、正方体
13、一个直立在水平面上的圆柱体的主视图、俯视图、左视图分别是 ( )
A长方形 、圆、长方形 B、长方形、长方形、圆
C、圆、长方形、长方形 D、长方形、长主形、圆
1、下面图形经过折叠不能围成棱柱的是 ( )

2、说法中,不正确的是( )
A、棱柱的侧面可以是三角形; B 棱柱的侧面展开图是一个长方形;
C、若一个棱柱的底面为5边形、则可知该棱柱侧面是由5个长方形组成的;
D、棱柱的上底面与下底面的形状与大小是完全一样的。
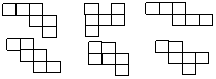 3、如图中是正方体的展开图的有(
)个
3、如图中是正方体的展开图的有(
)个
A、2个 B、3个 C、4个 D、5个
4、画出下列几何体的三视图。(5分)
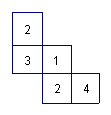
5、如图,这是一个由小立方块塔成的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数。请你画出它的主视图与左视图。(8分)
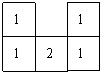 |
 6、已知下图为一几何体的三视图:(8分)
6、已知下图为一几何体的三视图:(8分)
(1)写出这个几何体的名称;
(2)任意画出它的一种表面展开图;
(3)若主视图的长为10![]() ,俯视图中三角形的边长为4
,俯视图中三角形的边长为4![]() ,求这个几何体的侧面积。
,求这个几何体的侧面积。
1、探索规律:用棋子按下面的方式摆出正方形(6分)
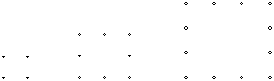 |
①按图示规律填写下表:
| 图形编号 | (1) | (2) | (3) | (4) | (5) | (6) |
| 棋子个数 |
②按照这种方式摆下去,摆第![]() 个正方形需要多少个棋子?
个正方形需要多少个棋子?
③按照这种方式摆下去,第第![]() 个正方形需要多少个棋子?
个正方形需要多少个棋子?
2、将一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱,现在有一个长为4cm、宽为3cm的长方形,分别绕它的长、宽所在直线旋转一周,得到不同的圆柱体,它们的体积分别是多大?(8分)
 3.正方体是由六个平面图形围成的立体图形,
3.正方体是由六个平面图形围成的立体图形,
设想沿着正方体的一些棱将它剪开,就可以
把正方体剪成一个平面图形,但同一个正方
体,按不同的方式展开所得的平面展开图是
不一样的,下面的图形是由6个大小一样的
正方形,拼接而成的,请问这些图形中哪些
可以折成正方体?试试看(8分)
1.已知:图(1)、图(2)分别是6×6正方形网格上两个轴对称图形(阴影部分),其面积分别为SA、SB(网格中最小的正方形面积为一个平方单位),请观察图形并解答下列问题.(9分)
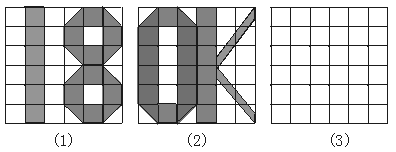
(1)填空:SA∶SB的值是__________;
(2)请你在图(3)的网格上画出一个面积为8个平方单位的中心对称图形.
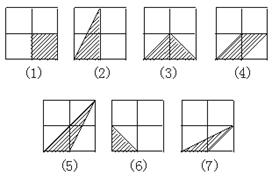
提示:如果没有规律性认识,要找出具有“美感”的图案是比较困难的,适当的方法是:选择一些图形作为基本图形,通过基本图形的组合,找出解答,所列的7个图形可认为是基本图形.
 请你再作出3个符合要求的图形.
请你再作出3个符合要求的图形.
 | |||
 | |||
.
 |
 趣味题:
趣味题:
图中写有一个“只”字,只要加上一笔就可以变为另外的一个汉字,
你知道该怎么加这一笔吗?变成了什么汉字?(请在图上直接加上一笔)
1.易拉罐类似于几何体中的______体,其中有____个平面,有____个曲面.
2.流星坠落会在空中留下一条______;转动的自行车的辐条(俗称“钢丝”)会形成一个________;一个长方形绕自身的一条边旋转会形成一个______.
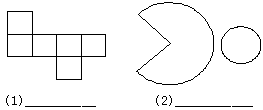
3.如下图是两个立体图形的展开图,请你写出这两个立体图形的名称:
 |
4.一个直角三角形绕它的一条直角边旋转一周形成的几何体是________.
5.一个正棱锥有六个顶点,所有侧棱长的和为30cm,则每条侧棱的长是______cm.
6.在一个正十一边形中,从一个顶点出发,分别连接这个顶点与其余各顶点,可以构成个_______个三角形.
 7.若圆柱的底面半径为r,高为h,将这个圆柱侧面展开后,得到一个长方形,则这个长方形的面积用r、h表示出来是:__________.
7.若圆柱的底面半径为r,高为h,将这个圆柱侧面展开后,得到一个长方形,则这个长方形的面积用r、h表示出来是:__________.
8.用一个平面去截一个正方体,截面可以是:
_________________________(要求至少写出4种)
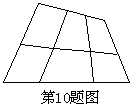
9.如右图所示,图中共有___________个四边形.
10.如果一个几何体的的主视图和左视图都是长方形,俯视图是圆,那么这个几何体可能是【 】
A.圆锥 B.棱柱 C.圆柱 D.球
11.右图中的几何体一共有【 】个面.
A.5 B.6 C.7 D.8
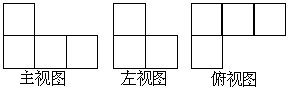 |
12.下图是由一些相同的正方体组成的几何体的三视图,组成这个几何体需要【 】个小正方体. A. 4 B.5 C.6 D.7
13.下列说法错误的是【 】
A. 三棱锥的截面一定是三角形 ; B.三棱柱的各个侧面是四边形;
C.若棱柱的底面边长相等,则它的各个侧面的面积相等;
D.圆柱体的截面中不一定有曲线.
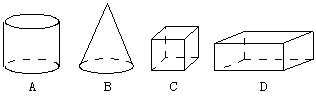 |
1.下列图形的主视图中,和其它的有明显不同的是【 】
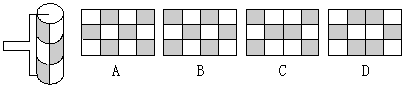 |
2.小华用如图所示的胶滚沿从右到左的方向将图案涂到墙上,下列给出的四个图案中符合胶滚涂出的图案的是【 】
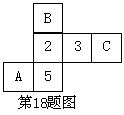 3.如图所示的图形,这是一个正方体的展开图,各个相对面的数字相同,则A、B、C面上的数字分别为【
】
3.如图所示的图形,这是一个正方体的展开图,各个相对面的数字相同,则A、B、C面上的数字分别为【
】
A.2,5,3 B.3,5,2
C.3,2,5 D.5,2,3
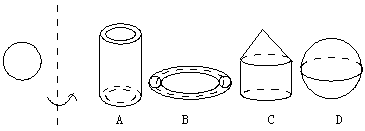 |
4.如图把一个圆绕虚线旋转一周,得到的几何体是【 】
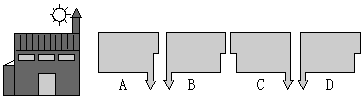
5.如图,太阳在房子的后方,那么房子在地面上的影子是【 】
 |
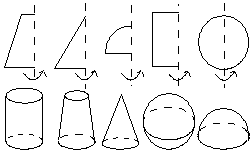 |
6.如图,把第一行的图形绕虚线旋转一周,便能形成第二行的某个几何体,请用线连起来.
1.如图是由几个小正方体堆成的几何体,请以如图所示的正面为主视方向画出它的主视图、左视图、俯视图.

 2.观察右边的表格,回答问题:
2.观察右边的表格,回答问题:
(1)表格中有哪些图形?___________________
(1) 你发现了什么样的变化规律?
________________________________________
(2) 图中有一处遗漏的图形,请你把它画出来.
3.请画出下列几何体的主视图、左视图、俯视图.

4.下图是由小正方体搭成的几何体的俯视图,正方体中的数字表示该位置小正方体的个数,请你画出这个几何体的主视图和左视图.
 |
1.长方体有________个顶点,有_______条棱,______个面,这些面的形状都是_______.
2.圆柱的侧面展开图是__________,圆锥的侧面展开图__________.
3.如果一个几何体的视图之一是三角形,这个几何体可能是___________(写出两个即可).
4.用平行于圆锥的底面的平面去截圆锥,则得到的截面是________形.
5.在同一平面内用游戏棒搭4个大小一样的等边三角形,至少要________根游戏棒;在空间搭4个一样大小的等边三角形,至少要________根游戏棒.
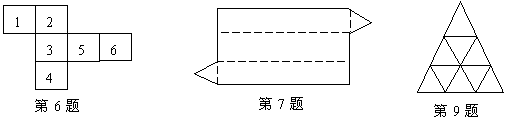 6.如图所示,将图沿虚线折起来,得到一个正方体,那么“3”的对面是_______(填编号).
6.如图所示,将图沿虚线折起来,得到一个正方体,那么“3”的对面是_______(填编号).
7.能展开成如图所示的几何体可能是____________.
8.图柱的侧面展开图是_________,圆锥的侧面展开图是_____________.
9.如图中,共有________个三角形的个数,________个平行四边形,_________个梯形.
10.一个多面体的面数为12,棱数是30,则其顶点数为_________.
11.面与面相交成______,线与线相交得到_______,点动成______,线动成_________,面动成_______.
12.一个几何体,是由许多规格相同的小正方体堆积而成的,某主视图、左视图如图所示,要摆成这样的图形,至少需用________块正方体,最多需用_________正方体.
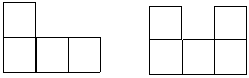 |
13.下列说法中,正确的是( )
A、棱柱的侧面可以是三角形
B、由六个大小一样的正方形所组成的图形是正方体的展开图
C、正方体的各条棱都相等
D、棱柱的各条棱都相等
14.用一个平面去截一个正方体,截面不可能是( )
A、梯形 B、五边形 C、六边形 D、圆
15.下列立体图形中,有五个面的是( )
A、四棱锥 B、五棱锥 C、四棱柱 D、五棱柱
16.将一个正方体截去一个角,则其面数( )
A、增加 B、不变 C、减少 D、上述三种情况均有可能
1.一个长为19cm,宽为18cm的长方形,如果把这个长方形分成若干个正方形要求正方形的边长为正整数,那么该长方形最少可分成正方形的个数( )
 A、5个
B、6个 C、7个 D、8个
A、5个
B、6个 C、7个 D、8个
2.一个正方形,六个面上分别写着六个连续的整数,且每个
相对面上的两个数之和相等,如图所示,你能看到的数为
7、10、11,则六个整数的和为( )
A、51 B、52 C、57 D、58
3.如图所示,是一个由小立方体搭成的几何体的俯视图,小正方形中数字表示该位置的小立方块的个数,则它的主视图为( )
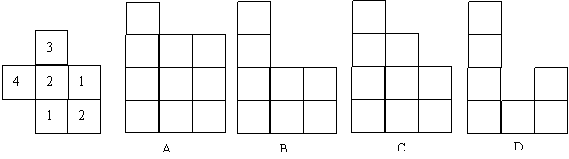
4.如图中是正方体的展开图的有( )个
 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个
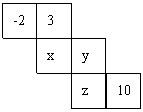 |
5. 若要使得图中平面展开图折叠成正方体后,
相对面上的两个数之和为5,求x+y+z的值.
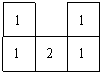
1.由六个小立方体搭成的几何体的俯视图如图所示,小正方体中的数字表示在该位置的小立方体的个数,请画出这个几何体的主视图和左视图.
2.用正方何小木块搭建成的,下面三个图分别是它的主视图、俯视图、和左视图,请你观察它是由多少块小木块组成的.
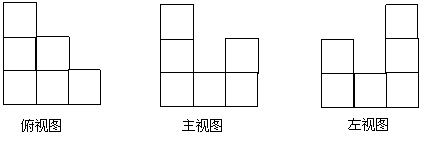 |
3.如图所示,这是两盏灯的图例,请你利用其中的构件(两个圆,两个三角形,两条平行线段)构造出新的思路独特而且有意义的图形,并加上合适的解说词,请你构造一个这样的图形。

4.推理猜测题:
(1)三棱锥有_______条棱,四棱锥有_______条棱,十棱锥有_________条棱;
(2)__________棱锥有30条棱;
(3)__________棱柱有60条棱;
(4)一个多面体的棱数是8,则这个多面体的面数是_________.
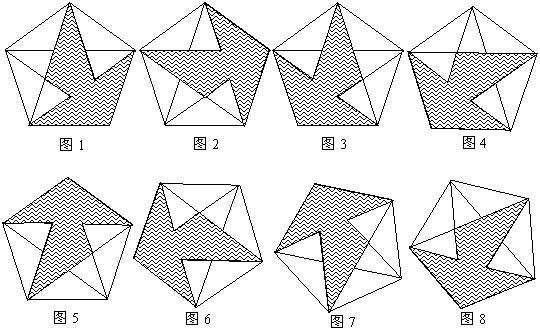
1.考眼力:这八幅图中只有一幅与众不同,你能在半分钟内把它找出来吗?与众不同是________.(填序号)
2.将一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱,现在有一个长为4cm、宽为3cm的长方形,分别绕它的长、宽所在直线旋转一周,得到不同的圆柱体,它们的体积分别是多大?
3.半圆面绕直径旋转一周形成__________.
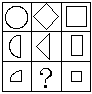
4.图1中按左侧三个图形阴影部分的特点,将右侧的图形补充完整.

图1
5.两条宽都为1 cm的纸条,交叉重叠放在一起,则它们重叠部分构成的图形为______,特殊的边可以是__________.
1.如图2,把边长为6 cm的正三角形纸板,剪去三个三角形,得到边长都相等的正六边形,作出模型量得此六边形的边长为_______________.
2.如图3,所示的正方体中过D点所作的截面三角形为_________(填写2个).
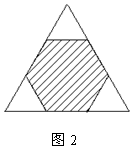
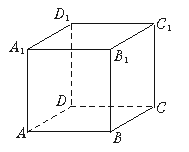
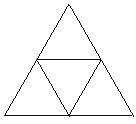
图3 图4
3.如图4,沿正三角形三边中点连线折起,可拼得一个_____________________.
4.如果某几何体它的俯视图、正视图及左视图都相同,则该几何体可能是_________.
5. 如图5,下面有一张大图,这张大图的右下方有一块空白,是要填空的.填什么,请看大图右方若干个标有数码的小图.它们的大小、形状与右下角空白处一样.请将你要填的图的数码号写入空白处,使大图成为一张图形完整、协调一致的图.
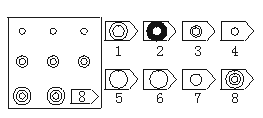
图5
6.用五个面围成的几何体可能是_______________.
7.如图6,将正方体沿面AB′C剪下,则截下的几何体(图7)为__________.
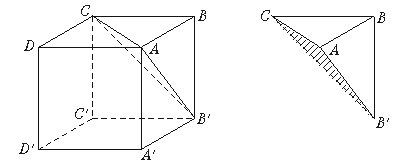
图6 图7
8.用平面去截一个几何体,如截面为矩形,则几何体不可能是( )
A.圆柱 B.圆锥 C.长方体 D.正方体
1.设“●”、“▲”、“■”表示三种不同的物体,现用天平称了两次,情况如图所示,![]()
![]() 那么●、▲、■这三种物体按质量从大到小的顺序排列应为( )
那么●、▲、■这三种物体按质量从大到小的顺序排列应为( )
A.■、●、▲; B.■、▲、●; C.▲、●、■; D.▲、■、●
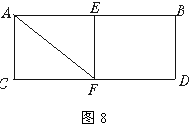 2.如图8,在矩形ABDC中,E、F分别为AB、CD的中点,现将矩形ACFE沿EF折线折起,则折叠前后线段AF变化情况为( )
2.如图8,在矩形ABDC中,E、F分别为AB、CD的中点,现将矩形ACFE沿EF折线折起,则折叠前后线段AF变化情况为( )
A.变化; B.不变化;
C.是否发生变化与矩形的边长有关; D.无法确定
3. 如图9,长方形ABCD中,E、G和F、H分别是DC与AB的三等分点.沿EF、GH将其折成一个无底三棱柱,则折叠后线段AC变为( )
A.两条折线; B.三条折线; C.AM、MN、NC构成三角形; D.以上都有可能
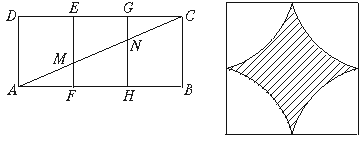
图9 图10
4.如图10,正方形的边长为1,分别以四个顶点为圆心,r为半径画圆,给中间涂色就得到如图所示的图案,则( )
A.r=1; B.r=![]() ; C.r=
; C.r=![]() ; D.r=
; D.r=![]()
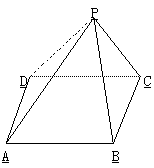 5.四棱锥的底面ABCD为正方形,且PA=PB=PC=PD,现将其沿侧棱PA、PB、PC、PD剪开,并以底边为折线将其向外放到底面上,画出图形.
5.四棱锥的底面ABCD为正方形,且PA=PB=PC=PD,现将其沿侧棱PA、PB、PC、PD剪开,并以底边为折线将其向外放到底面上,画出图形.
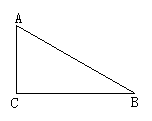
1.三角形ABC为直角三角形,现将三角形ABC补成矩形,使三角形ABC的两个顶点为矩形一边的两个端点,第三个顶点落在矩形这一边的对边上,画出符合要求的矩形.
2.正方体是由六个平面图形围成的立体图形,设想沿着正方体的一些棱将它剪开,就可以把正方体剪成一个平面图形,但同一个正方体,按不同的方式展开所得的平面展开图是不一样的,下面的图形是由6个大小一样的正方形,拼接而成的,请问这些图形中哪些可以折成正方体?试试看.

3.是由几个小立方块搭成的几何体的俯视图,小正方形的数字表示该位置小立方块的个数,请画出相应的几何体的主视图及左视图.
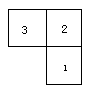
1.将下列几何体分类,柱体有: ,锥体有 (填序号) ;
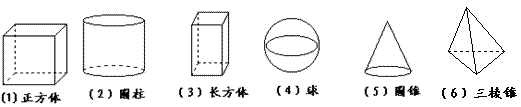
2.圆柱的底面是 ,侧面是 ,展开后的侧面是 ;
3.圆锥的底面是 ,侧面是 ,展开后的侧面是 ;
 4.棱柱的侧面是
,分为 棱柱和
棱柱;
4.棱柱的侧面是
,分为 棱柱和
棱柱;
5.如图1-1中的几何体有 个面,面面相交成 线;
6.把一块学生使用的三角板以一条直角边为轴旋转成的
形状是 体形状;
7.薄薄的硬币在桌面上转动时,看上去象球,这说明了____ _____________.
 8.六棱柱有 个顶点,
个面;
8.六棱柱有 个顶点,
个面;
9.若要使图中平面展开图按虚线折叠成正方体后,相
对面上两个数之和为6,x=_ ___,y=______.
 10.如图,四个三角形均为等边三角形,将图形折叠,得到的立体图形是 ( )
10.如图,四个三角形均为等边三角形,将图形折叠,得到的立体图形是 ( )
A. 三棱锥 B. 圆锥体 C. 棱锥体 D. 六面体
11. 用一个平面去截一个正方体,截面不可能是
A.梯形 B.五边形 C.六边形 D.圆
12.下面的图形中,是三棱柱的侧面展开图的为 ( )
A. B.
B.  C.
C.  D.
D.
13.用一个平面去截①圆锥;②圆柱;③球;④五棱柱,能得到截面是圆的图形是 ( )
A.①②④ B.①②③ C.②③④ D.①③④
14.从多边形一条边上的一点(不是顶点)发出发,连接各个顶点得到2003个三角形,则这个多边形的边数为( )
A、2001 B、2005 C、2004 D、2006
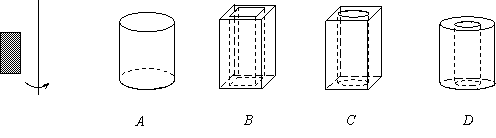 15.观察下图,请把左边的图形绕着给定的直线旋转一周后可能形成的几何体选出来( )
15.观察下图,请把左边的图形绕着给定的直线旋转一周后可能形成的几何体选出来( )
1. 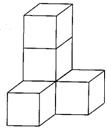 下图是由五块积木搭成,这几块积木都是相同的正方体,请画出这个图形的主视图、左视图和俯视图。
下图是由五块积木搭成,这几块积木都是相同的正方体,请画出这个图形的主视图、左视图和俯视图。
2. 如图是几个正方体所组成的几何体的俯视图,小正方形中的数字表示该位置小正方块的个数.请画出这个几何体的主视图和俯视图.
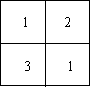 |
3、推理猜测题:(每题3分,共12分)
 (1).三棱锥有______条棱,四棱锥有______条棱,十棱锥有______条棱;
(1).三棱锥有______条棱,四棱锥有______条棱,十棱锥有______条棱;
.______棱锥有30条棱;
(2).一个多面体的棱数是8,则这个多面体的面数是______.
(3). 如右上图所示,电视台的摄像机1、)(4)在不同位置拍摄了四幅画面,则A图象是______号摄像机所拍,B图象是______号摄像机所拍,C图象是______号摄像机所拍,D图象是______号摄像机所拍。
4、将一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱,现在有一个长为4厘米,宽为3厘米的长方形,分别绕它的长、宽所在的直线旋转一周,得到不同的圆柱体,它们的体积分别是多大?
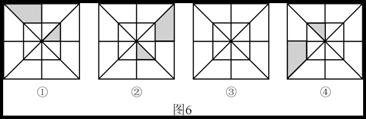
1.(2004年四川资阳)分析图6①,②,④中阴影部分的分布规律,按此规律在图6③中画出其中的阴影部分.
2.水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”
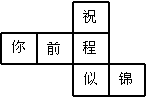 表示.如右图,是一个正方体的平面展开图,若图中的“似”表示正
表示.如右图,是一个正方体的平面展开图,若图中的“似”表示正
方体的前面, “锦”表示右面, “程”表示下面.则“祝”、
“你”、 “前”分别表示正方体的___________________________
________________________.(04潍坊)
3圆锥是由____个面围成,其中有____个平面,_____个曲面。
4.将一个硬币立在桌面上用力一转,它形成的是一个_______体,由此说明_______________。
5.在棱柱中,任何相邻的两个面的交线都叫做______,相邻的两个侧面的交线叫做_______。
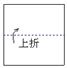
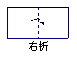
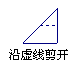
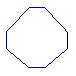
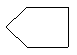
6如图,把一个正方形三次对折后沿虚线剪下则得到的图形是_____.(04河南)




 (A)
(B)
(C) (D)
(A)
(B)
(C) (D)
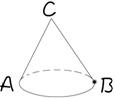
7如图,在圆锥底面圆周B点有一只蚂蚁,要从圆锥体侧面爬一圈后,再回到B点,请你结合圆锥的展开图设计一条最短路径。
1、从一个多边形的某个顶点出发,分别连接这个点和其余各顶点,可以把这个多边形分割成十个三角形,则这个多边形的边数为___ __。
2、伟大的数学家欧拉发现并证明的关于一个多面体的顶点(V)、棱数(E)、面数(F)之间关系的公式为_______________,一个n面体共有8条棱,5个顶点,则n=_____。
3、写出两个三视图形状都一样的几何体:____ ___、_________。
4、一个长方形长为4厘米,宽为2厘米,以它的长边为轴,把长方形转一周后,得到一个_____体,这个立体图形的体积是________立方厘米。(结果中保留π)
5、在桌面上摆有一些大小一样的正方体木块,主视图(1),俯视图(2),要摆出这样的图形至多需用__________块正方体木块,至少需用_________块正方体木块。
 | 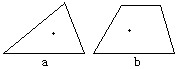 |
(第8题) (第9题) (第10题)
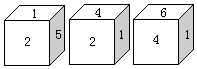
6、已知一不透明的正方体的六个面上分别写着1至6六个数字,如图是我们能看到的三种情况,那么1和5的对面数字分别是____和_____。
7、(1) 如图(a),在三角形内取一点,与三角形的三条边可以组成____个三角形.
(2) 如图 (b),在四边形内取一点,与四边形的四条边可以组成_______个三角形.
(3) 在n边形(n为不小于3的自然数)内取一点,与n边形的每条边可以组成_______个三角形。
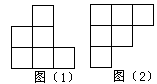
8、在下列几何体中,不能展开成平面图形的是( )
A、棱柱 B、圆柱 C、圆锥 D、球
9、下面几何体的截面图不可能是圆的是( )
A、圆柱 B、圆锥 C、球 D、棱柱
10、一个直立在水平面上的圆柱体的主视图、俯视图、左视图分别是( )
A、长方形、圆、长方形 B、长方形、长方形、圆
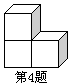 C、圆、长方形、长方形 D、长方形、长主形、圆
C、圆、长方形、长方形 D、长方形、长主形、圆
11、将半圆绕它的直径旋转一周形成的几何体是( )
A、圆柱 B、圆锥 C、球 D、正方体
![]() 12、如图,该物体的俯视图是( )
12、如图,该物体的俯视图是( )
![]()
![]()
![]() A、
B、
C、
D、
A、
B、
C、
D、
13、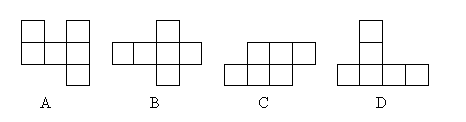 下列图形是正方体的展开图的是( )
下列图形是正方体的展开图的是( )
1、若一个立体图形的主视图与左视图都是等腰三角形,俯视图是圆,则这个图形可能是( )
A.圆台 B.圆柱 C.圆锥 D.三棱锥
2、一只蚂蚁从如图正方体的一顶点A沿着棱爬向B,只能经过三条棱,共有多少种走法( )
A.8种 B.7种 C.6种 D.5种
3、将n边形的一个顶点与其他(不相邻的)连结起来,这样的对角线的条数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4、如果由小正方体组成的模型中白色的面正对着你,请你画出它的三视图

(主视图) (左视图) (俯视图)
5、画出如图所示的几何体的主视图和左视图。
![]()
![]()
![]() 3 4 2
3 4 2
![]() 2 1
2 1
(俯视图)
6、请你尝试用圆、扇形、多边形、直线等几何图形为2008年奥运会设计一个有意义的画面,并用优美的语言表达你所创作的作品的含义。
7你为下面这个图形再添加两个小正方形,使它能拼成一个正方体。(尽可能的多)
![]()
![]()
![]()
![]()
![]()
![]()
1、 

 已知下图为一几何体的三视图:(1)写出这个几何体的名称;(2)任意画出它的一种表面展开图;(3)若主视图的长为10cm,俯视图中三角形的边长为4cm,求这个几何体的侧面积。
已知下图为一几何体的三视图:(1)写出这个几何体的名称;(2)任意画出它的一种表面展开图;(3)若主视图的长为10cm,俯视图中三角形的边长为4cm,求这个几何体的侧面积。
主视图:长方形 左视图:长方形 俯视图:等边三角形
 2、如图,已知一个矩形,其长是宽的两倍。请你把这矩形剪成:
2、如图,已知一个矩形,其长是宽的两倍。请你把这矩形剪成:
(1) 两部分,使得它们能够拼成一个等腰三角形;
(2) 两部分,使得它们能够拼成一个直角三角形;
(3) 三部分,使得它们能够拼成一个正方形。



3看下图,这些图经过折叠可以围成一个棱柱吗?想一想,亲自动手折一折。

(1) (2) (3)
1如右图是一多面体的展开图,每个面内都标注了字母,请根据要求回答问题
(1) 如果面A在多面体的底部,那么哪一面会在上面?
(2) 如果面F在前面,从左面看是面B,那么哪一面会在上面?
(3)
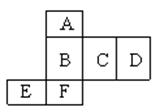 从右面看是面C,面D在后面,那么哪一面会在上面?
从右面看是面C,面D在后面,那么哪一面会在上面?
分析 (1)面F;(2)面C ;(3)面A
说明 这是一个长方形的表面展开图,共有6个面,其中面A与面C、E、F相同,根据所处位置可知面A与面F相对,面C与面E相对,面B与面D相对。(1)中,面A在长方体的底部,那么它所对的面F就应该在上面;(2)中面F在前面,面B在左面,那么它们所对的面A就在后面,面D就在右面,所以面C应该在上面,而面E在底部;(3)中面C在右面,那么面E就在左面,面D在后面,那么面B就在前面,所以此时面F在底部,而面A则应该在上面。
2.如图(1)所示,该图是某立体图形从正面看,从左面看,从上面看得到的平面图形,该立体图形的名称是_______。

3.计算:(1)78°32′-51°47°=_______· (2)23°45′+24°20′=_______·
4.已知线段AB,在BA的延长线上取一点C,使CA=3AB,则CB=_______AB,CA=_______CB.
5.如果两个角互补,并且它们的差是30°,那么较大的角等于_______·
6.时针指示6点45分,它的时针和分针所成的锐角度数是_______·
7.已知:∠AOB=40°,OC是∠AOB的平分线,则∠AOC的余角度数是_______·
8.如图(2)所示,点B到直线AC的距离是_______, CD的长度是_____到线段______的距离.
9.数一数图(3)中共有_______个三角形.



10.如图(4)所示,射线OA表示的方向是_______,射线OB表示的方向是_______·
11.平面上画出四条直线,交点的个数最多有( )
A.5个 D。6个 C.7个 D.8个
1.如图是用4个长方体搭成的图形,从左面看,它应是下列图形中的( )





2.下列说法中错误的有( )
(1)线段有两个端点,直线有一个端点
(2)角的大小与我们画出的角的两边的长短无关
(3)线段上有无数个点
(4)同角或等角的补角相等
(5)两个锐角的和一定大于直角
A.1个 B.2个 C.3个 D.4个
3.在如图所示中,∠α与∠β为对顶角的是( )




4.如图(5)所示,O在直线m上,∠1与∠2互余,∠α=134°,则∠β的度数是( )
A.134° B.136° C.154° D.156°


![]()
5.如图(6)中,下列表示不正确的是( )
A.AB+BC=AC B.∠C=45° C.∠B+∠B=180° D.∠1+∠2=∠ADC
6.如图(7)所示,M是AB上一点,AM=8cm,BM=2cm,N是AB的中点,则MN的长为( )
A.1cm B.2cm C.3cm D.4cm
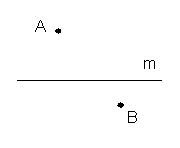 1.如图,直线m表示一条河,在河两侧有两个村庄A、B,要在河边建一个供水站,使供水站到两个村庄的距离之和最小,请找出C点位置,并说明理由.
1.如图,直线m表示一条河,在河两侧有两个村庄A、B,要在河边建一个供水站,使供水站到两个村庄的距离之和最小,请找出C点位置,并说明理由.
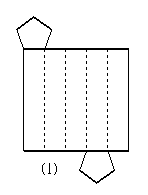
2.想一想,哪种几何体的表面展开成如下的平面图形,画出表示这些几何体的立体图形.
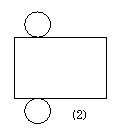
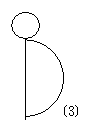
3.已知线段AB上两点C、D,其中AB=acm,CD=bcm,E、F分别是AC、DB的中点.
(1)求AC+DB的长度;(2)E、F两点间的距离.
4.如图,O是直线AB上的点,OD是∠AOC的平分线,OE是∠COB的平分线.
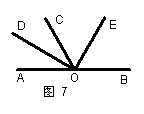 (1)求∠DOE的度数;(2)若∠DOE=90°,OD平分∠AOC,问OE是否平分∠BOC?
(1)求∠DOE的度数;(2)若∠DOE=90°,OD平分∠AOC,问OE是否平分∠BOC?
5.已知:一个角的补角加上10°后,等于这个角的余角的3倍,求:这个角及其余角和补角的度数.
1.如图,观察图形,填空:包围着体的是______;面与面相交的地方形成______; 线与线相交的地方是_______.
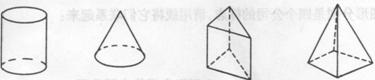
 2.笔尖在纸上快速滑动写出了一个又一个字,这说明了_________;车轮旋转时,看起来像一个整体的圆面,这说明了_________;直角三角形绕它的直角边旋转一周,形成了一圆锥体,这说明了_____________.
2.笔尖在纸上快速滑动写出了一个又一个字,这说明了_________;车轮旋转时,看起来像一个整体的圆面,这说明了_________;直角三角形绕它的直角边旋转一周,形成了一圆锥体,这说明了_____________.
3.如图,三棱锥有________个面,它们相交形成了________条棱, 这些棱相交形成了________个点.
4.如图,各图中的阴影图形绕着直线I旋转360°,各能形成怎样的立体图形?
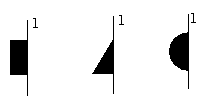
 5.小明用如图所示的胶滚沿从左到右的方向将图案滚涂到墙上,下列给出的4个图案中,符合图示滚涂出的图案是( )
5.小明用如图所示的胶滚沿从左到右的方向将图案滚涂到墙上,下列给出的4个图案中,符合图示滚涂出的图案是( )
6.生活中经常看到由一些简单的平面图形组成的优美图案, 你能说出下面图中的神秘图案是由哪些平面图形组成的吗?

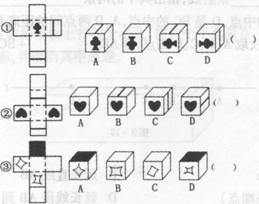 7.将如图左边的图形折成一个立方体, 判断右边的四个立方体哪个是由左边的图形折成的.
7.将如图左边的图形折成一个立方体, 判断右边的四个立方体哪个是由左边的图形折成的.
8.用6根火柴能摆成含有4个三角形的图形吗?有几种方法?
1.小明为班级专栏设计一个图案,如图,主题是“我们喜爱合作学习”, 请你也尝试用圆、扇形、三角形、四边形、直线等为环保专栏设计一个图案, 并标明你的主题.
2图(1)是棱长为1的小正方体,图(2)、图(3)是由这样的正方体摆放面成,按照这样的方法继续摆放,自上而下分别叫第1层、第2层……第n层,第n层的小正方体个数记为S;解答下列问题:
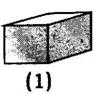
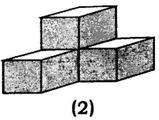
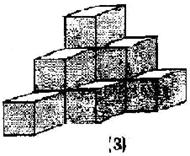
(1)按要求填表:
| n | 1 | 2 | 3 | 4 | …… |
| 1 | 3 | 6 | ? | …… |
(2)写出当n=10时,S=__________
3.如图,在∠AOB的内部引一条射线OC,可得几个小于平角的角? 引两条射线OC、OD呢?引三条射线OC、OD、OE呢?若引十条射线一共会有多少个角?
4.请用直线、线段、角等图形设计成表示客观事物的图画,如图, 并为你的图画命名.
1.经过一点,有______条直线;经过两点有_____条直线,并且______条直线.
2.如图1,图中共有______条线段,它们是_________.
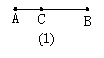
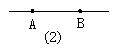
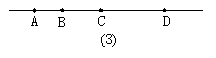
3.如图2,图中共有_______条射线,指出其中的两条________.
4.线段AB=8cm,C是AB的中点,D是BC的中点,A、D两点间的距离是_____cm.
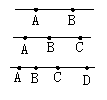
5.如图3,在直线I上顺次取A、B、C、D四点,则AC=______+BC=AD-_____,AC+BD- BC=________.
6.下列语句准确规范的是( )
A.直线a、b相交于一点m B.延长直线AB
C.反向延长射线AO(O是端点) D.延长线段AB到C,使BC=AB
7.下列四个图中的线段(或直线、射线)能相交的是( )

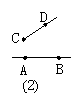
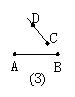
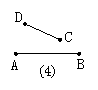
A.(1) B.(2) C.(3) D.(4)
 8.如果点C在AB上,下列表达式①AC=
8.如果点C在AB上,下列表达式①AC=![]() AB;②AB=2BC;③AC=BC;④AC+BC=AB中, 能表示C是AB中点的有( )
AB;②AB=2BC;③AC=BC;④AC+BC=AB中, 能表示C是AB中点的有( )
A.1个 B.2个 C.3个 D.4个
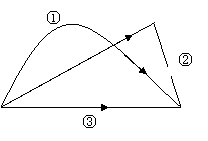
9.如图,从A到B有3条路径,最短的路径是③,理由是( )
A.因为③是直的 B.两点确定一条直线
C.两点间距离的定义 D.两点之间,线段最短
10.如图,平面上有四个点A、B、C、D,根据下列语句画图
(1)画直线AB、CD交于E点;
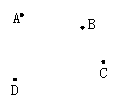 (2)画线段AC、BD交于点F;
(2)画线段AC、BD交于点F;
(3)连接E、F交BC于点G;
(4)连接AD,并将其反向延长;
(5)作射线BC;
(6)取一点P,使P在直线AB上又在直线CD上.
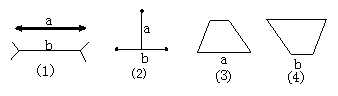 11.观察图中的3组图形,分别比较线段a、b的长短,再用刻度尺量一下, 看看你的结果是否正确.
11.观察图中的3组图形,分别比较线段a、b的长短,再用刻度尺量一下, 看看你的结果是否正确.
1.如图,要在一个长方体的木块上打四个小孔,这四个小孔要在一条直线上,且每两个相邻孔之间的距离相等,画出图形,并说明其中道理.

2.如图,一个三角形纸片,不用任何工具,你能准确比较线段AB与线段AC的大小吗?试用你的方法分别确定线段AB、AC的中点.

3.在一条直线上取两上点A、B,共得几条线段?在一条直线上取三个点A、B、 C,共得几条线段?在一条直线上取A、B、C、D四个点时,共得多少条线段? 在一条直线上取n个点时,共可得多少条线段?
9.分别确定四个城市相应钟表上时针与分钟所成的角的度数.

1.下列关于角的说法正确的个数是( )
①角是由两条射线组成的图形;②角的边越长,角越大; ③在角一边延长线上取一点D;④角可以看作由一条射线绕着它的端点旋转而形成的图形.
A.1个 B.2个 C.3个 D.4个
2.下列4个图形中,能用∠1,∠AOB,∠O三种方法表示同一角的图形是( )
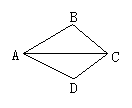
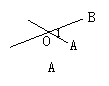
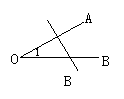
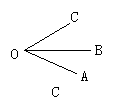
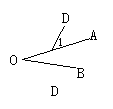
3.图中,小于平角的角有( )
A.5个 B.6个 C.7个 D.8个
二、填空:
4.将一个周角分成360份,其中每一份是______°的角,
直角等于____°,平角等于______°.
5.30.6°=_____°_____′=_______′;30°6′=_______′______°.
三、解答题:
6.计算:
(1)49°38′+66°22′; (2)180°-79°19′; (2)22°16′×5; (4)182°36′÷4.
7.根据下列语句画图:
(1)画∠AOB=100°;
(2)在∠AOB的内部画射线OC,使∠BOC=50°;
(3)在∠AOB的外部画射线OD,使∠DOA=40°;
(4)在射线OD上取E点,在射线OA上取F,使∠OEF=90°.
8.任意画一个三角形,估计其中三个角的度数的和,
再用量角器检验你的估计是否准确.
10.九点20分时,时钟上时钟与分钟的夹角a等于多少度?