第二章 有理数的概念
班级: 姓名:
1.把下列各数分类:
1,![]() ,8.2,-7,
,8.2,-7,![]() ,0,-3.5,1008,-0.5,-10
,0,-3.5,1008,-0.5,-10
2.当a﹤0时,![]() ;
;![]() 的相反数是 ,绝对值为5的数是 ,相反数为3的数为 。
的相反数是 ,绝对值为5的数是 ,相反数为3的数为 。
3.绝对值不大于4的整数是 。绝对值不大于4的整数的和是 。
4.![]() 的倒数与
的倒数与![]() 的相反数的差等于
。
的相反数的差等于
。
5.满足![]() 的数有 个,他们是
;满足
的数有 个,他们是
;满足![]() 的数有 个,他们是
的数有 个,他们是
;满足![]() 的数有 个。
的数有 个。
6.若![]() ,则
,则![]() 。
。
7.在数轴上与数-1所对应的点相距2个单位长度的点表示的数为 ,长为2个单位长度的木条放在数轴上,最多能覆盖 个点。
8.已知a﹥0,b﹤0,︱a︱﹤︱b︱,用“﹤”符号把![]() ,
,![]() ,
,![]() ,
,![]() 连接起来的式子为
。
连接起来的式子为
。
9.如果![]() ,那么
,那么![]() 。
。
10.若![]() 、
、![]() 互为相反数,
互为相反数,![]() 、
、![]() 互为倒数,有理数
互为倒数,有理数![]() 在数轴上的对应点到原点的距离为1,则代数式
在数轴上的对应点到原点的距离为1,则代数式![]() 的值是
。
的值是
。
11.若![]() ,若
,若![]() 0,若
0,若![]() ,若
,若![]() 0。
0。
12.一个有理数与它的倒数相等,这样的有理数是 。
13.下列说法正确的是( )
A.正数和负数互为相反数。 B.数轴上,原点两旁的两个点所表示的数是互为相反数
C.除0以外的数都有它的相反数。 D.任何一个数都有它的相反数。
14.下列说法正确的是( )
A.绝对值等于它本身的数一定是正数 B.最大的负数是-1
C.整数是由正整数和负整数所组成的 D.有限小数是有理数
15.已知![]() ,
,![]() ,求
,求![]() 的值。
的值。
16.有理数![]() 、
、![]() 在数轴上的对应点如图所示,则下列结论错误的是
在数轴上的对应点如图所示,则下列结论错误的是
![]()
![]()
![]() A. ︱b︱﹥-a B. ︱a︱﹥-b C. b﹥a D.
︱a︱﹥︱b︱
A. ︱b︱﹥-a B. ︱a︱﹥-b C. b﹥a D.
︱a︱﹥︱b︱
![]()
![]() 17.已知
17.已知![]() ,求
,求![]() 、
、![]() 的值。
的值。
![]()
![]() 0
0
18.当 -2﹤x﹤5时,化简![]() 。
。
19.如果![]() ,
,![]() ,
,![]() ,那么
,那么![]() ,
,![]() 。
。
20.绝对值小于10的所有的整数的和是 ,积是 。
21.已知![]() ,
,![]() ,
,![]() ,则
,则![]() 的值为
。
的值为
。
22.若![]() ,式子
,式子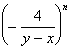 的值(
的值(![]() 为整数)是
。
为整数)是
。
23.若![]() ,计算代数式:
,计算代数式:
![]()
24.如果收入20元记作+20元,那么-75元表示 。
25.如果-30%表示减少30%,那么+50%表示 。
26.求下列各数的相反数:
(1)-5 (2)![]() (3)0 (4)
(3)0 (4)![]() (5)
(5)![]() (6)
(6)![]() (7)
(7)![]()
27.大于-4.5的非正整数有 个,大于-7.6且小于2.9的整数有 个。
28.![]() 是 的相反数,若
是 的相反数,若![]() ,则
,则![]() 。
。
29.绝对值最小的数是 ,绝对值等于![]() 的数是
。
的数是
。
30.绝对值小于3的整数有 个,它们是 。
31.已知![]() ,
,![]() ,则
,则![]() 。
。
32.若![]() ,则
,则![]() 0。
0。
33.已知![]() ,求
,求![]() 的值。
的值。
34.已知 a﹤0, b﹤0,且︱a︱﹤︱b︱,试用“﹤”号将![]() 、
、![]() 、
、![]() 、
、![]() 连接起来。
连接起来。
35.小明同学每天早上6:00钟开始起床,起床穿衣的时间需要5分钟,起床后他立即用煤气灶煮早饭,早饭一共需要7分钟才能煮熟,他洗脸、漱口时间需要5分钟,吃早饭需要8分钟,吃完早饭就去上学,小明同学很会合理安排时间,他从开始起床到吃完早饭仅需要 分钟,请你以后在生活中实践一下。
36.如果 a﹥0,b﹤0,且a+b﹤0,则( )
A. ︱a︱﹥︱b︱ B.![]() C. ︱a︱﹤︱b︱
D. ︱b︱﹤0
C. ︱a︱﹤︱b︱
D. ︱b︱﹤0
37.已知![]() ,则
,则![]() 的值为
。
的值为
。
38.绝对值不大于4的整数的和是 。
39.如果a﹤0, b﹤0,,且︱a︱﹥︱b︱,那么![]() 是(
)
是(
)
A. 正数 B. 负数 C. 0 D. 以上都有可能
40.0减去![]() 的相反数,结果是
。
的相反数,结果是
。
41.若![]() ,
,![]() ,且a﹥0,b﹤0,则
,且a﹥0,b﹤0,则![]() 。
。
42.![]() 的绝对值与
的绝对值与![]() 的相反数的差是
。
的相反数的差是
。
43.已知![]() ,则
,则![]() 。
。
44.![]() ,则
,则![]() 。
。
45.若![]() ,则
,则![]() 。
。
46.下列说法正确的是( )
A. 几个有理数相乘,当负因数有奇数个时,积为负。
B. 几个有理数相乘,当负因数有偶数个时,积为正。
C. 几个有理数相乘,当积为负数时,负因数有奇数个。
D. 几个有理数相乘,当因数有偶数个时,积为正。
47. 求![]() 的所有可能的值。
的所有可能的值。
48 –54 的底数是 ,它表示 。
49. ![]() ,
, ![]()
50.若![]() 、
、![]() 互为倒数,
互为倒数,![]() 、
、![]() 互为相反数,
互为相反数,![]() ,
,![]()
51.![]() ,
,![]() 。
。
52.四个互不相等的整数![]() 、
、![]() 、
、![]() 、
、![]() 的积是9,则
的积是9,则![]() 。
。
53.已知![]() 与
与![]() 互为倒数,
互为倒数,![]() 与
与![]() 互为相反数,且
互为相反数,且![]() ,求
,求![]() 的值。
的值。
54.绝对值大于6小于13的所有负整数的和是 。
55.如果a+b﹥0,并且![]() 、
、![]() 异号,b﹥a,则
异号,b﹥a,则![]()
![]() 。
。
56.如果![]() ,x﹥0,那么
,x﹥0,那么![]() 。
。
57.![]() 的底数是
,指数是
。
的底数是
,指数是
。
![]() 58.
58. ![]() 。
。
![]()
注意:
0的相反数是它本身,0属于整数,属于有理数,0的任何次幂都等于本身,0既不是正数也不是负数,它是有理数,0没有倒数。0是绝对值最小的有理数。
1的平方和立方都等于本身,1的倒数也等于本身,1是最小的正整数。
-1的立方等于本身,平方等于它的相反数,-1是最大的负整数。
两个负数比较大小时,先比较它们的绝对值,绝对值大的反而小,即为反号。
两个正数比较大小时,就直接用小学的通分法比较大小,不反号.
混合运算时,要注意运算顺序,先乘方,后乘除,最后再加减,如果有括号,就先算括号里的,一步一步来,注意除数要变为它的倒数,并带上它本身的符号,计算是本章的重点。
