典型例题

　　例1  判断下面的移项对不对，如果不对，应怎样改正？

　　（1）从 得到 ；

　　（2）从 得到 ；

　　（3）从 得到 ；

　　（4）从 得到 ；

　　分析： 判断移项是否正确，关键看移项后的符号是否改变，一定要牢记“移项变号”．注意：没有移动的项，符号不要改变；另外等号同一边的项互相调换位置，这些项的符号不改变．

　　解：（1）不对，等号左边的7移到等号右边应改变符号．正确应为：

　　（2）对．

　　（3）不对．等号左端的－2移到等号右边改变了符号，但等号右边的 移到等号左边没有改变等号．正确应为：

　　（4）不对．等号右边的 移到等号左边，变为 是对的，但等号右边的－2仍在等号的右边没有移项，不应变号．正确应为：

　　选题角度：关于利用移项法则判断移项是否正确的题目

　　例2 判断下列各式哪些是一元一次方程．

　　（1） ；（2） ；（3） ；

　　（4） ；（5） ；（6）

　　分析： 判断一个数学式子是不是一元一次方程，首先看它是不是方程，其次再看它含有几个未知数，并且未知数的最高次数是多少．

　　解：（1）是，因为 是方程，且方程只含有一个未知数 ，且含未知数的项最高次数是1．

　　（2）不是． 不是方程．

　　（3）不是．因为 虽然是方程但含有两个未知数 、 ．

　　（4）不是．因为 不是方程．

　　（5）不是．因为 含有两个未知数．

　　（6）不是．因为 中未知数最高次数为2次．

　　例3 解方程：

　　（1） ；（2）

　　（3） ；（4）

　　分析： 本题都是简单的方程，只要根据等式的性质2．把等号左边未知的系数化为1，即可得到方程的解．

　　解：（1）把 的系数化为1，根据等式的性质2．在方程两边同时除以3得，

　　检验 左边 ，右边

　　左边=右边．

　　所以 是原方程的解．

　　（2）把 的系数化为1，根据等式的性质2，在方程两边同时除以4得， ．

　　检验：左边 ，右边=2，

　　左边=右边

　　所以 是原方程的解．

　　（3）把 的系数化为1．根据等式性质2，在方程的两边同时乘以 得，

　　

　　

　　检验，左边

　　右边

　　左边=-右边，

　　所以 是原方程的解；

　　（4）把 的系数化为1，根据等式的性质2，在方程两边同时乘以－2得：

　　

　　

　　检验：左边 ，右边 ，

　　左边=右边．

　　所以 是原方程的解．

　　说明： ①在应用等式的性质2把未知数的系数化为1时，什么情况适宜用“乘”，什么情况下适宜用“除”，要根据未知数的系数而定．一般情况来说．当未知数的系数是整数时，适宜用除；当未知数的系数是分数（或小数）适宜用乘．（乘以未知数系数的倒数）．②要养成进行检验的习惯，但检验可不必书面写出．

　　选题角度：关于判断方程是不是一元一次方程的题目

　　例4　解方程

　　分析：题给方程不是一元一次方程的标准形式，我们利用移项法则把含x的项全部移到等式左边，把常数项全部移到等式右边．转化成标准形式就容易求解了．

　　解：移项，得

　　合并同类项，得

　　方程两边同除以一5，得 。

　　例5 解方程：

　　（1） ；（2） ；

　　（3） ；（4）

　　分析： 解方程的思路是将已知方程通过一系列变形化为最简方程 的形式，也就是说把 作为已知方程变形的目标．因此，要把已知方程转化为最简化，就要把含有未知数的项都移到等号的一边，常数项移到等号的另一端．

　　解法一：（1）移项，得：

　　

　　合并同类项，得：

　　（2）移项，得

　　合并同类项，得　，

　　系数化成1，得，　

　　解法二，移项，得，

　　 ，

　　合并同类项，得：

　　

　　系数化为1，得，

　　

　　（3）移项，得：

　　

　　合并同类项，得

　　

　　系数化为1，得

　　

　　（4）移项，得：

　　

　　合并同类项，得，

　　

　　系数化为1，得

　　

　　说明： 第（2）题采用了两种不同的移项方法，目的都是将未知数的项移到等号的一端，已知数移到等号另一端，事实上，其它的题目也都可以采用不同的移项方法，要根据题目的特点，寻找简捷的移项方法．

　　例6　解方程

　　分析：本题的特征是方程含有小括号，这就启发我们先从去括号入手。

　　解：去括号，得

　　整理得

　　移项，得

　　合并，得

　　两边同除以30，得

　　选题角度：关于解系数系数都是整数的一元一次方程

习题精选

　　一、选择题

　　1．下列各方程中，属于一元一次方程的是（　  ）

　　A． 　 B． 　　C． 　　D．

　　2．下列方程中，是一元一次方程的是（）

　　A． 　　 B．

　　C． 　　D．

　　3．方程 是一元一次方程，那么a的值是（　　）

　　A．0　　B．-1　　C．0或1　 D．1

　　4．方程 移项后，正确的是（）

　　A． 　　B．

　　C． 　　D．

　　5．方程 去分母得（　　 ）

　　A． 　　　B．

　　C． 　　 D．

　　6．方程 的解是（　　 ）

　　A．4　　 B．2　　 C．1　　 D．0

　　7．如果 那么 的值是（　　）

　　A．20　　B．30　　 C．40　　 D．-10

　　8．方程 去分母后，正确的是（）

　　A． 　　B．

　　C． 　　D．

　　9．关于 的方程 与 是同解方程，那么 的值是（）

　　（A）10　 （B）9　　 （C）8　　（D）3

　　10．方程 的解是（）

　　（A） 　　（B） 　　（C） 　 （D）

　　11．如果方程 的解是0，那么 的值等于（）

　　（A） 　　（B） 　　（C） 　 （D）

　　12．下列去分母错误的是（）

　　（A） ，去分母得

　　（B） ，去分母得

　　（C） ，去分母得

　　（D） ，去分母得

　　13．方程 的解是（）

　　（A） 　　（B）

　　（C） 　　 （D）

　　二、填空题

　　1．解方程中移项变号的根据是_________；

　　2．一元一次方程的标准形式是_________；

　　3．解一元一次方程的一般步骤有_________；

　　4．方程 的解是_________；

　　5．方程 的解是_________；

　　6．方程 的解是_________；

　　7．方程 的解是_________；

　　8．方程 的解是_________；

　　9．方程 的解是_________；

　　10．解方程 去分母，得_________；

　　11．已知关于x的方程 是一元一次方程，则 为_____，n为______;

　　12．当 时，代数式 与代数式 的值互为相反数;

　　13．已知当 时，四次三项式 的值为5，则 时，它的值是______;

　　14．如果 ，那么 ___________；

　　15．如果 ，那么 ___________；

　　16．如果 ，那么 ___________；

　　17．已知 ，那么代数式 的值是___________.

　　18．在方程 ， ， ， ， 中是一元一次方程的为_________；

　　19．方程 的解是________；

　　20．方程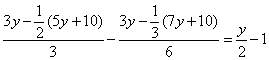 的解是___________.

　　三、解答题

　　1．解方程：

　　（1） ；（2） ；

　　（3） ；（4） ；

　　（5） ；（6）

　　2．解方程：

　　（1） ；

　　（2） ；

　　（3） ；

　　（4） ；

　　3．解方程：

　　（1） ；（2） ；

　　（3）；（4）

　　4．解方程：

　　（1） ；

　　（2） ；

　　5．解方程：

　　（1） ；（2） ；

　　（3） ；（4）

　　6．解下列方程：

　　（1）

　　（2）

　　（3）

　　（4）

　　（5）

　　（6）

　　（7）

　　7．解方程

　　（1） ；

　　（2） ；

　　（3） ；

　　（4） ；

　　（5） ；

　　（6）

　　8．解关于 的方程：

　　（1） ；（2）

　　（3） ；（4）

　　9．根据下列条件列出方程，然后求出某数。

　　（1）某数的 比它的相反数小5；

　　（2）某数与3的差的一半比9与这个数的差少6；

　　（3）某数与－6的差的3倍等于这个数的相反数；

　　（4）某数的7倍与10%的和恰好是它的5%与3的差。

　　10．（1） 取何值，代数式 与 的值相等？

　　（2） 取何值，代数式 与 的值相等？

　　11．解关于x的方程：

　　12．如果方程 与 的解相同，求m的值。（△）

　　13．已知 ，且 ，求代数式 的值。

　　14． 为何值时，关于x的方程 的解：

　　（1）有唯一的解？（2）没有解？

　　15．已知关于x的方程 和方程 有相同的解，求a的值及这个相同的解。（△）

　　16．方程 与 的解相同，求 的值。

　　17．若 ，代数式 的值比 多1，求 的值。

　　18．解关于 的方程

　　19．已知方程 与方程 都是关于 的方程且两个方程的解相同，求它们的解及相应 的值。

　　20．（1）已知关于 的方程 的解是－4，求 的值；

　　（2）已知方程 的解与关于 的方程 的解相同，求代数式 的值。

　　21．梯形面积公式 中：

　　（1）已知S、 、 求 ；（2）已知S、 、 求 。

　　22．求出适合下列等式的未知数的值：

　　（1） ；

　　（2） ；

　　（3）

　　23．代数式 的值与代数式 的值互为相反数，求 的值。

　　24．在梯形面积公式 中，已知 ， ， ，求 。

　　25．解方程：

　　26．解方程：

　　27．已知关于 的方程 的解与 的解相等，求 的值。

　　28．把方程 化成两个一元一次方程，并分别求出它们的解。

　　研究题：

　　若 ，解关于 的方程：

　　答案：

　　一、1．D 2．D 3．D　4．C 5．C　 6．C　 7．C． 8．B　9. A；10. C；11. B；12. B； 13. D.

　　二、1．等式的性质1；　　2． ；

　　３．去分母，去括号，移项，合并同类项，系数化1。

　　４． ；５． ；６． ；７． ；

　　８． ；９． ；10．

　　11．不为2；2或0　12．   13．-7 .

　　14． ；15． ； 16． ； 17．24 .

　　18. ; . 19. x=5 ; 20. .

　　三、1．解方程：

　　（1） ；（2） ；（3） ；（4） ；

　　（5） ；（6）

　　2．解方程：

　　（1） ； （2） ；（3） ；（4）

　　3．解方程：

　　（1） ；（2） ；（3） ；（4）

　　4．解方程：

　　（1） ；（2）

　　5．解方程：

　　（1） ；（2） ；（3） ；（4）

　　6．（1） ；（2）；（3）；（4）；

　　（5） ；（6） ；（7） 或

　　7．（1） ；（2） ；（3） ；

　　（4） ；（5） 或；（6） 或

　　8．（1） ；（2） ；（3） ；

　　（4）当 时， ，当 时， 为任意有理数。

　　9．根据下列条件列出方程，然后求出某数。

　　（1） ， ；

　　（2） ；

　　（3） ；

　　（4）

　　10．（1） ；（2）

　　11．当 时，方程有无数个解，即为任意数；当 时，方程的解为   12．

　　13．-8　 14．（1） ；（2） 　　15．由 解得 ；由 解得 ，依两方程的解相同，有 解得 ，故 · 。

　　16．121．提示：由 得 ，由于 的解与 的解相同，所以有 ，从而有

　　17．0．由 得 又因为 的值比 多1，所以有 ，将 代入上式可解得

　　18．由 ，得

　　∵   ∴   ∴

　　19． ，得 ；由 ，得； ；

　　根据题意，有 解之，得 ，∴

　　20．（1） ; （2）

　　21．（1） ;　（2）

　　22．（1） 且 ； （2） 且 ；（3） 且

　　23． ；　24．

　　25． 　　26．   27．   28．

　　研究题：

　　略解

　　　　 ，

　　　　

　　　　

　　所以