初一数学“命题、定理与证明”练习
1、判断下列语句是不是命题
（1）延长线段AB（ ）
（2）两条直线相交，只有一交点（ ）
（3）画线段AB的中点（ ）
（4）若x=2，则x=2（ ）
（5）角平分线是一条射线（ ）
2、选择题
（1）下列语句不是命题的是（ ）
A、两点之间，线段最短 B、不平行的两条直线有一个交点
C、x与y的和等于0吗？ D、对顶角不相等。
（2）下列命题中真命题是（ ）
A、两个锐角之和为钝角 B、两个锐角之和为锐角
C、钝角大于它的补角 D、锐角小于它的余角
（3）命题：①对顶角相等；②垂直于同一条直线的两直线平行；③相等的角是对顶角；④同位角相等。其中假命题有（ ）
A、1个 B、2个 C、3个 D、4个
3、分别指出下列各命题的题设和结论。
（1）如果a∥b，b∥c，那么a∥c
（2）同旁内角互补，两直线平行。
4、分别把下列命题写成“如果……，那么……”的形式。
（1）两点确定一条直线；
（2）等角的补角相等；
（3）内错角相等。
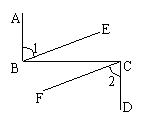
5、已知：如图AB⊥BC，BC⊥CD且∠1=∠2，求证：BE∥CF
证明：∵AB⊥BC，BC⊥CD（已知）
∴ = =90°（ ）
∵∠1=∠2（已知）
∴ = （等式性质）
∴BE∥CF（
）
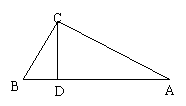
6、已知：如图，AC⊥BC，垂足为C，∠BCD是∠B的余角。
求证：∠ACD=∠B。
证明：∵AC⊥BC（已知）
∴∠ACB=90°（ ）
∴∠BCD是∠DCA的余角
∵∠BCD是∠B的余角（已知） ∴∠ACD=∠B（ ）
7、已知，如图，BCE、AFE是直线，AB∥CD，∠1=∠2，∠3=∠4。
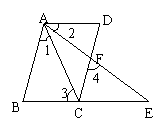求证：AD∥BE。
证明：∵AB∥CD（已知）
∴∠4=∠ （ ）
∵∠3=∠4（已知）
∴∠3=∠ （ ）
∵∠1=∠2（已知）
∴∠1+∠CAF=∠2+∠CAF（ ）
即∠ =∠
∴∠3=∠ （ ）
∴AD∥BE（ ）
 |
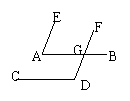8、已知，如图，AB∥CD，∠EAB+∠FDC=180°。
求证：AE∥FD。
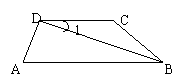9、已知：如图，DC∥AB，∠1+∠A=90°。
求证：AD⊥DB。
 |
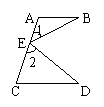
10、如图，已知AC∥DE，∠1=∠2。
求证：AB∥CD。
 |
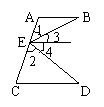
11、已知，如图，AB∥CD，∠1=∠B，∠2=∠D。
求证：BE⊥DE。
12、求证：两条平行直线被第三条直线所截，内错角的平分线互相平行。
【练习答案】
1、（1）不是 （2）是 （3）不是 （4）是 （5）是
2、（1）C （2）C （3）B
3、（1）题设：a∥b，b∥c结论：a∥c
（2）题设：两条直线被第三条直线所截的同旁内角互补。
结论：这两条直线平行。
4、（1）如果有两个定点，那么过这两点有且只有一条直线
（2）如果两个角分别是两个等角的补角，那么这两个角相等。
（3）如果两个角是内错角，那么这两个角相等。
5、∠ABC=∠BCD，垂直定义，∠EBC=∠BCF，内错角相等，两直线平行。
6、垂直定义；余角定义，同角的余角相等。
7、∠BAE 两直线平行同位角相等
∠BAE （等量代换） 等式性质
∠BAE，∠CAD，∠CAD（等量代换）
内错角相等，两直线平行。
8、证明：∵AB∥CD
∴∠AGD+∠FDC=180°（两直线平行，同旁内角互补）
∵∠EAB+∠FDC=180°（已知）
∴∠AGD=∠EAB（同角的补角相等）
∴AE∥FD（内错角相等，两直线平行）
9、证明：∵DC∥AB（已知）
∴∠A+∠ADC=180°（两直线平行，同旁内角互补）
即∠A+∠ADB+∠1=180°
∵∠1+∠A=90°（已知）
∴∠ADB=90°（等式性质）
∴AD⊥DB（垂直定义）
10、证明：∵AC∥DE（已知）
∴∠2=∠ACD（两直线平行，内错角相等）
∵∠1=∠2 （已知）
∴∠1=∠ACD（等量代换）
∴AB∥CD（内错角相等，两直线平行）
11、证明：作EF∥AB
∵AB∥CD
∴∠B=∠3（两直线平行，内错角相等）
∵∠1=∠B（已知）
∴∠1=∠3（等量代换）
∵AB∥EF，AB∥（已作，已知）
∴EF∥CD（平行于同一直线的两直线平行）
∴∠4=∠D（两直线平行，内错角相等）
∵∠2=∠D（已知）
∴∠2=∠4（等量代换）
∵∠1+∠2+∠3+∠4=180°（平角定义）
∴∠3+∠4=90°（等量代换、等式性质）
即∠BED=90°
∴BE⊥ED（垂直定义）
12、已知：AB∥CD，EG、FR分别是∠BEF、∠EFC的平分线。
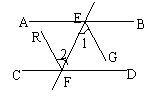求证：EG∥FR。
证明：∵AB∥CD（已知）
∴∠BEF=∠EFC（两直线平行，内错角相等）
∵EG、FR分别是∠BEF、∠EFC的平分线（已知）
∴2∠1=∠BEF，2∠2=∠EFC（角平分线定义）
∴2∠1=2∠2（等量代换）
∴∠1=∠2（等式性质）
∴EG∥FR（内错角相等，两直线平行）