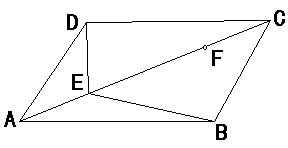| 三角形四边形练习题 |
| 一、填空 |
| 1、若凸n边形的内角和等于360°,则n=________。 |
| 2、用长为100cm的铁丝制成一个矩形,其面积为625cm  ,那么这个矩形的对角线长_____cm。 ,那么这个矩形的对角线长_____cm。 |
|  3、 如图,已知 3、 如图,已知 , , , , ,则 ,则 _________。 _________。
|
| 4、已知四边形ABCD的对角线AC与BD相交于点O,若 , , ,则四边形ABCD的面积最小值为_____。 ,则四边形ABCD的面积最小值为_____。 |
|  5、 如图,三角形纸片ABC中, 5、 如图,三角形纸片ABC中, , , ,将纸片的一角折叠,使C落在 ,将纸片的一角折叠,使C落在 ABC 内, ABC 内, ,将纸片的一角折叠,使点C落在 ,将纸片的一角折叠,使点C落在 内,若 内,若 ,则 ,则 为_______度。 为_______度。
|
| 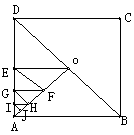 6、如图,在正方形ABCD 中,AD 6、如图,在正方形ABCD 中,AD OE, FG, HI, 都垂直于AD, EF, GH, I J都垂直于AO, 若已知 OE, FG, HI, 都垂直于AD, EF, GH, I J都垂直于AO, 若已知 ,则S正方形ABCD=_____。 ,则S正方形ABCD=_____。
|
|  7、如图在 7、如图在 ABC中,BC=a, ABC中,BC=a,  , , 是AB边的五等分点, 是AB边的五等分点, 是AC边的五等分点,则 是AC边的五等分点,则 ——。 ——。
|
| 8、已知三个数1、2、 ,请你再添上一个数(只填一个)使它们构成一个比例式,则这个数是_______。 ,请你再添上一个数(只填一个)使它们构成一个比例式,则这个数是_______。 |
| 10、如图,在 ABC中, ABC中, ACB= ACB= ,CD⊥AB, 垂足为D, AD=6, BD=2, 则CD的长是_____ 。 ,CD⊥AB, 垂足为D, AD=6, BD=2, 则CD的长是_____ 。 
|
| 11、把直角三角形ABC的斜边AB放在垂直线t 上,按顺时针方向在t 上转动两次,使它转到 的位置,设BC=1,AC= 的位置,设BC=1,AC= ,则顶点A运动到 ,则顶点A运动到 位置时,点A经过的路线与直线t 所围成的面积是_______(计算结果可求近似值) 位置时,点A经过的路线与直线t 所围成的面积是_______(计算结果可求近似值) |
| 二、选择 |
| 1、 如图已知梯形ABCD中,AD∥BC, 如图已知梯形ABCD中,AD∥BC,  , , ,AB=8则CD的长为( ) ,AB=8则CD的长为( ) A、 B、 B、 C、 C、 D、 D、 |
| 2、如图:E是边长为1 的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q, PR⊥BE于点R,则PQ+PR的值为( )
A、 B、 B、 C、 C、 D、 D、 
|
| 3、如图,在等边 ABC中,P为BC上一点,D为AC上一点,且 ABC中,P为BC上一点,D为AC上一点,且 ,BP=1, CD= ,BP=1, CD= ,则 ,则 ABC的边长为( ) ABC的边长为( )
A、3 B、4 C、5 D、6 
|
| 4、如图,已知矩形ABCD,R,P分别是DC、BC上的点,E、F分别是AP、RP的中点,若P在BC上从B向C移动,而R不动时,那么下列结论成立的是( )
A、 线段EF的长逐渐增大
B、 线段EF的长逐渐减小
C、 线段EF的长不改变
D、线段EF的长不能确定 |
| 5、将一张平行四边形纸片折一次,使该折痕平分这个平行四边形的面积,则这样的折纸方法共有( )
A、1种 B、2种 C、4种 D、无数 |
| 6、如图,在 ABC中,AB=24, AC=18, D是 ABC中,AB=24, AC=18, D是 AC上一点,AD=12,在AB上取一点E,使A、D、E三点组成的三角形与 AC上一点,AD=12,在AB上取一点E,使A、D、E三点组成的三角形与 ABC相似,则AE的长为( ) ABC相似,则AE的长为( )
A、16 B、14 C、16或14 D、16或9 |
| 三、大题 |
| 1、如图1,梯形ABCD中,AD∥BC,AB=DC,
①如果P、E、F分别是BC、AC、BD的中点,求证:AB=PE+PF。
②如果P是BC上任一点(中点除外)PE∥AB,PF∥DC,如图2,那么AB=PE+PF这个结论还成立吗?若成立给出证明,若不成立,请明理由。 (北京2003) |
| 2,如图,在平形四边形ABCD中,点E、F在对角线AC上,且AE=CF,请你以F为一个端点,和图中已标明字母的某一点连成一条新线段,猜想并证明它和图中已有的一条线所相等(只须证明一组线段相等即可)
(1).连结__________ 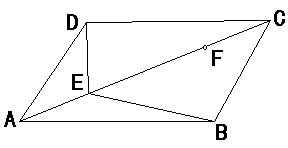
(2).猜想_________=__________
(3).证明你的猜想 (江苏2003) |
| 3、已知:如图D是AC上一点,BE∥AC,BE=AD,AE分别是BD、BC于点F、G、∠CAF=∠CBD 
(1).图中哪几个三角形与 FAD全等?证明你的结论。 FAD全等?证明你的结论。
(2).求证: =FG•EF =FG•EF (河南2003) |
| 4,已知:如图,在Rt ABC 中, ABC 中, ACB=90 ACB=90 ,AC=BC,D为BC的中点,CE⊥AD,垂足为点E,BF∥AC交CE的延长线于点F,求证:AB垂直平分DF。 ,AC=BC,D为BC的中点,CE⊥AD,垂足为点E,BF∥AC交CE的延长线于点F,求证:AB垂直平分DF。 (福州2003) |
| 5,已知:如图,等边 ABC中,AB=2, 点P是AB边上的任一点,(点P可以与点A重合,但不与点B重合),过点P作PE ABC中,AB=2, 点P是AB边上的任一点,(点P可以与点A重合,但不与点B重合),过点P作PE BC,垂足为E; 过点E作EF BC,垂足为E; 过点E作EF AC; 垂足为F,过点F作FQ AC; 垂足为F,过点F作FQ AB,垂足为Q,设BP=X, AQ=Y AB,垂足为Q,设BP=X, AQ=Y
(1) 写出Y与X之间的函数关系式。
(2) 当BP的长等于多少时?点P与点Q重合?
(3) 当线段PE、FQ相交时,写出线段PE、EF、FQ所围成三角形的周长的取值范围(不必写出解题过程) |
 3、 如图,已知
3、 如图,已知 5、 如图,三角形纸片ABC中,
5、 如图,三角形纸片ABC中,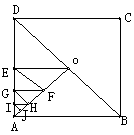 6、如图,在正方形ABCD 中,AD
6、如图,在正方形ABCD 中,AD 7、如图在
7、如图在
 如图已知梯形ABCD中,AD∥BC,
如图已知梯形ABCD中,AD∥BC, 


 AC上一点,AD=12,在AB上取一点E,使A、D、E三点组成的三角形与
AC上一点,AD=12,在AB上取一点E,使A、D、E三点组成的三角形与