七年级（上）期末复习检查题（1）

（华师大课标版）

一、填空题

1.(1)填空:(在括号里填出每一步运算的依据)

(a×b)²=(a×b)×(a×b)(　　　　 )

=a×b×a×b=a×a×b×b(　　　　 )

=(a×a)×(b×b)(　　　 )

=a²×b²(　　　　)

(2)试用上面方法推导出:①(a×b)³=a³×b³②(a×b)ⁿ=aⁿ×bⁿ(n为正整数)

(3)根据上面推导的结果计算:

①[26×(-)]³×(-)³;

②3²ⁿ×()²ⁿ⁺¹(n为正整数);

③10²ⁿ⁺¹×(0.1)²ⁿ⁺¹(n为正整数).

2. 下面是一个立体图形的三视图，你觉得这个立体图形是________．

主视图　　 俯视图　　 左视图

3. 在题后横线上填上"必然发生"或"不可能发生"或"可能发生"，掷两个普通的正方体骰子，把两个骰子的点数相加：

①和为1：　　　　　 ；②和为6：　　　　　　 ；③和为12：　　　　　 ；

④和为14：　　　　　 ；⑤和大于2：　　　　　 ；⑥和小于2：　　　　　 ；

⑦和小于20：　　　　　

4. 探索规律：

（1）当有两个确定的点时，可以画出一条线段；

（2）当有三个确定的点时，可以画出_______条线段；

（3）当有四个确定的点时，可以画出_______条线段；

（4）如此计算，当n个确定的点时，可以画出_______条线段.

5. "外错角"的故事

我们知道，研究直线之间的位置关系时，往往是通过研究它们所成的角实现的.

如我们在课堂上学的：用一条直线去截两条直线，如果截得的同位角、内错角、同旁内角之间有相等或互补的关系时，这两条直线就互相平行.

事实上，我们也可通过其它的角来判定两条直线平行.如图，直线AB、CD被直线EF所截，∠1与∠2分别在直线AB、CD上、下两侧，并且∠1在直线EF的左侧，∠2在直线EF的右侧，像这样的一对角叫做外错角.

下面，请你利用已有的方法来推出"外错角相等，两直线平行"这个结论.

因为∠2=∠3（　　　　  ），

又因为∠1=∠2（已知），

所以∠　　　　=∠　　　　（等量代换），

所以　　　　∥　　　　（　　　　  ，两直线平行）.

我们已经知道了"外错角相等，两直线平行"这个结论，那么相应地，两条平行线的外错角是否相等呢？我们利用已经学过的平行线的特征来进行下面的推理.

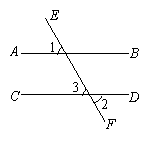如图，因为AB∥CD（已知），

所以∠1=∠ 　　　 （两直线平行，　　　　），

又因为∠2=∠3，

所以　　　　=　　　　（等量代换）.

二、选择题

1. 2 的相反数与绝对值是2 的数的差是 (　　).

（A） － 　（B） －5　 （C） － 或－5 （D） 或5

2. 若ab≠0，那么＋的值不可能是（　　）

（A）－2　（B）0　　（C）1  （D）2

3. 已知育英中学初一（1）班的同学去观看运动会的球类比赛，现由全班同学投票决定去看某两种球类的比赛，结果如下：假如你是班干部，你将怎样安排学生，才能使你班参加人数最多？（　　  ）

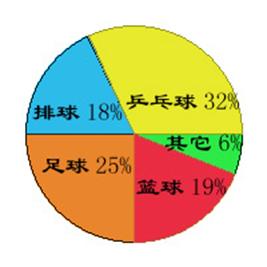（A）两部分分别看篮球和足球　

（B）两部分分别看篮球和排球

（C）两部分分别看乒乓球和足球

（D）两部分分别看排球和足球

4. 如果a－b=0,则a、b的关系是(　　 )

（A） 互为相反数；

（B） a= b,且b≥0;

（C） 相等且都不小于0；

（D） a是b的绝对值.

5. a－b＜0.的条件是（　　 ）

（A）a、b都是正数　（B）a、b都是负数 （C）a、b一正一负　 （D）a比b小

三、解答题

1. 在1，2，3，4，…，2004各数前面任意添加"+"或"－"号，然后求和，可以得到最小的非负值是多少.

2. 已知a－c=2，b－c=－3，求a+b－2c的值.

3. 词人苏轼有一句传诵千古的名句："横看成岭侧成峰，远近高低各不同."①请用简洁的几何图形勾画出这句话所表达的情境.②同学们一起交流一下这句话给我们的启示，特别谈谈对我们学习数学知识有何启迪.

4. 试说明两个有理数的和仍是有理数．

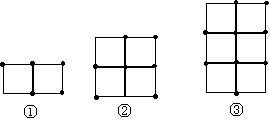5. 用火柴棒按下面的方式搭图形:

(1)填写下表:

(2)第n个图形需多少根火柴棒?

参考答案

一、填空题

1. (1)乘方的意义,乘法交换律,乘法结合律,乘方的意义;

(2)略;（3）；；-1

2. （三棱柱）

说明：这个三棱柱是像如图这样摆放的：

3. 不可能；可能；可能；不可能；可能；不可能；必然

4. （2）3，（3）6，（4）n(n-1)；

5. 对顶角相等，1，3，AB，CD，同位角相等，3，同位角相等，∠1，∠2

二、选择题

1. C；2. C；3. C；4. B；5. D

三、解答题

1. 0；（提示，任意4个连续整数n，n+1，n+2，n+3，总可以得到0，比如，－n－(n+3)+(n+1)+(n+2)=0，把1，2，…，2004，每4个一组，便可得到501个0，所以，最小的非负数为0）

2. －1

3. ①略；②各抒己见吧！

^{4. 设两个有理数分别是、，其中a,b,c,d为整数，且b≠０,d≠０.}

^{因为+=且两个整数的和与积仍是整数，所以ad＋bc与bd都为整数，所以是有理数，即+是有理数．}

5．（1）略；(2)5n+2