典型例题
例1 用代数式表示图中阴影部分面积S，并求当
时阴影部分面积S（
取
）．
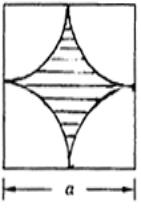
分析 为了方便，可分别设正方形、扇形面积
、
，由图可知：
，进一步利用面积公式就可求出结果．
解：
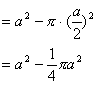
当 时，
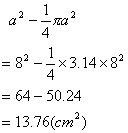
答：当 时阴影部分面积为
．
说明：计算此类阴影部分面积，常采取“叠加法”或“割补法”．要注意这种“聚零为整，化整为零”的思想方法在解题中的应用．
例2 已知梯形的上底是
，下底是
，高是
，面积是S．若
，
．求下底 ．
解：根据加与减，乘与除互为逆运算
由
，得
，
，
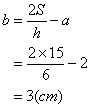
答：所求梯形的下底 为
．
说明：解此类题时，可先根据加与减，乘与除互为逆运算将公式变形，再由变形后的公式进行计算．
例3 某电影院有20排座位，已知第一排有18个座位，后面一排前一排多2个座位．写出计算第
排的座位数
的公式，并求第19排的座位数．
分析 可将排数与对应的座位数列表如下：
| 排数 | 每排座位数 |
| 1 2 3 4 5 … | 18 20 22 24 26 … |
第一排为
个座位；第二排有
个座位；第三排有
个座位……，由此可知座位数 与排数
之间的关系．
解：座位数 与排数 之间关系为：
当
时，
说明：此题需从反映数量关系的一些数据中分析出公式，进而求代数式的值，其中包含“由特殊到一般，又由一般到特殊”的思维方法，解题时要注意体会．
例4 某校气象兴趣小组为了研究气温随海拔高度变化的关系，在学校附近的一座小山上实地测量了不同高度的气温，测得结果如下表：
| 海拔高度 | 气温 |
| 0 | 20 |
| 100 | 19．4 |
| 200 | 18．8 |
| 300 | 18．2 |
| 400 | 17．6 |
（1）写出用海拔高度 表示气温
的公式；
（2）计算450米海拔高度时的气温．
分析：从表中可以看出：海拔高度每升高100米，气温就下降0．6摄氏度．而
，
，
，
，
……
且 
因此，上面各等式中右边“－”号后部分是
．用20减去 ，即是气温 ．
解：由题意，可得
（1）
；
（2）当
米时，
（摄氏度）．
答：450米海拔高度时的气温为17．3摄氏度．
说明：通过本例可以看出，公式并不是从天上掉下来的，而是通过“试验——观察——分析——寻求规律”的方法而发现的，反映了一种从特殊到一般的归纳思想，以及“由特殊到一般，由一般到特殊”的认识论方法．这些方法在今后的学习中必须重视．
例5 用代数式表示如图1-1阴影部分面积．
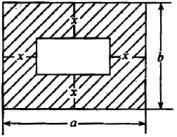
分析：阴影部分的面积可视为两个长方形的面积之差．也可以分割成几个小长方形或正方形，它们的面积和即为所求．
解法1：把阴影部分面积视为图中外长方形与内长方形的面积之差．
则 
解法2：把阴影部分割成两个长为 、宽为
与两个长为（
）、宽为 的长方形，
则 
.
说明：解决这种问题，主要是把所求图形，制补成一些基本的规则图形（能直接利用面积公式求解的图形），就很容易根据要求，把所求面积用代数式表示出来．当然，要注意割补合理、巧妙，从而确定出最佳方案，以最快的速度求出阴影部分的面积．
另外，上述两种解法得到的结果虽然形式上不一样，但是经过化简，实质上是一样的．
选题角度：
大体分这几类：一、用代数式表示图中阴影部分面积 ；二、 研究气温随海拔高度变化的关系；三、 用代数式表示电影院的每排座位数与排数的关系；四、用常见的公式求值，如梯形面积公式、长方形的面积公式等等。
习题精选
一、填空题
1．如图1-4-3，在长方形两边各以其宽为直径作半圆，正中紧贴两半圆作一个圆，则图中阴影部分的面积
________（用 、 、
表示）．
2．观察下列等式：
，
，
，
，…，则第 个等式用 表示为_______．
3．一个圆环，外圆半径为
cm，内圆半径为
cm，则圆环的面积
的公式为：
_________．此公式中，若用 、 、 表示
的结果应为：
=_______．
4．有一列数：
，
，
，
，…，则这一列数的第 个数为____________；这一列数中前100个数的和为_________．
5．下面由火柴杆拼出的一列图形中，第 个图形由 个正方形组成；
……观察发现．第四个图形中火柴杆有________根；第 个图形中有火柴杆________根．
参考答案
1．
；
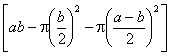2．
；
3．
， 
；
4．
，
；
5．13 
．
二、选择题
1．梯形的上底长1厘米，高为5厘米，面积是20平方厘米，则下底长为（ ）．
A．7厘米 B．3厘米
C．7厘米或3厘米 D．不能确定
2．正方形的棱长为a，则它的表面积S为（ ）．
A．a
B．4a
C．6a
D．8a
3．小红每天要做
道课外习题，第一天用了 小时，第二天用了 小时，则小红这两天平均每小时做的习题数 为（ ）．
A．
B．
C．
D．
4．长方形的长为 ，面积为 ，则其周长
用 、 表示的结果为（ ）．
A．
B．
C．
D．
5．李阳将压岁钱100元存入银行，存款的月利率是
，到期取出时，其本息和
元与所存月数 之间的关系为（不计利息税）（ ）．
A．
B．
C．
D．
6．三角形的两边为 、 ，其上的高分别为
、
，则用 、 、 表示 的结果为（ ）．
A．
B．
C．
D．
7．销售活动中，
. 某商人有一进价为450元的商品，要使利润率不低于10％，则售价最少应为（ ）．
A．495元 B．500元 C．545元 D．550元
参考答案：1．A 2．C 
3．C 4．D 5．D
6．B 7．A
三、解答题
1．球从高处自由落下，用仪器测得1秒末下落5米，2秒末下落20米，3秒末下落45米；用下落时间t(秒)表示下落的距离h(米)，写出这个公式．
2．根据给出的数据推导公式．
推导从1到 这 个连续自然数的和
的公式，并求当
时， 的值．
3．已知：两圆的直径和为30，其中一个圆的半径为R．
（1）用代数式表示2个圆的面积之和；
（2）当
时，求2个圆的面积之和．
4．梯形的上底是 ，下底是 ，面积是 ．如果
，
，
，求高 ．
5．一根钢管，它的截面是一个圆环，外圆直径
厘米，内圆直径
厘米，钢管长
米．求这个钢管的体积
．
6．如图，在长方形
中，
是
边的中点，两个直角扇形的半径分别为 与 ．设图中阴影部分的面积为 ．
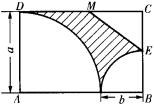
（1）求用 、 、 表示 的公式；（2）当
，
，
时，求 的值．
7．某商店出售一种商品，重量 与售价 之间的关系如右表：
| 数量 | 售价 |
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| … | … |
（1）写出用数量 表示售价 的公式．
（2）小张想买此种商品7.5千克，应付款多少元？
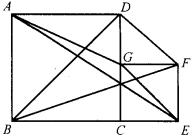
8．如图，已知正方形 的边长为 ，正方形
的边长为
，三角形
、
的面积分别记作
、
，试用两种方法求出用 、 表示 、 的公式．
9．钢铁厂工人堆放某种型号的圆柱形钢管的方法是：在最下面第一层先排 根，以后每层均比其下面的一层少一根钢管．第 层有
根钢管，这一堆钢管总数为
．
（1）写出用 、 表示 、 的公式，并说明当第一层排放了30根钢管时，这堆钢管最多有多少层？
（2）若钢铁厂某周生产此种钢管345根，受仓库高的限制只能堆放15层，则最下面一层应排放多少根？
参考答案：
1． 
．
2． 
．
当 时，
．
3．（1）设半径为R的圆的面积为
，则另一圆的面积为
，则；
．
（2）当 时，
，
∴ 
．
4．由题意，
．∴
4．答：所求梯形的高是 4．
5．由题意，可得
（立方厘米）．
6．（1）
（2）
．
7．（1）
（2）
元．
8．方法一：
，
方法二：延长
、
交于 ，
则 ，
．
9．（1）
（2）30层
（3）30根．