典型例题

　　例1　下列各图中，表示数轴的是(　　)．

　　

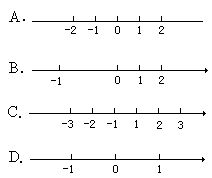
　　分析：画数轴时，数轴的三要素——原点、正方向、单位长度是缺一不可的，所以应当用这三要素检查每个图形，判断是否画的正确．

　　解：A图没有指明正方向；

　　　　B图中，1和-1表示的一个单位长度不相等，在同一数轴上，单位长度必须一致；

　　　　C图中没有原点；

　　　　D图中三要素齐全．

　　　　∴A、B、C三个图画的都不是数轴，只有D图画的是数轴．

　　例2　在所给的数轴上画出表示下列各数的点：

　　

　　

　　分析：第一步画数轴，第二步在数轴上找出相对应的点，每个正有理数都可用数轴上原点右边的一个点来表示，例如2、3.5，可用数轴上分别位于原点右边2个单位，3.5个单位的点表示．每一个负有理数都可用数轴上原点左边的一个点来表示，

　　解：

　　

　　说明：数轴上表示数的点可用大写字母标出，写在数轴上方所对应数的上面，原点用O标出，它表示数0．数轴上原点的位置要根据需要来确定，不一定要居中．单位长度应根据需要来确定，1 cm的长度可以表示1个单位长度，也可以表示2个，5个，10个…单位长度，但在同一数轴上，单位长度必须一致，不可随意改变．

　　例3　指出数轴上A、B、C、D、E各点分别表示什么数．

　　

　　分析：表示正数的点都在原点的右侧，表示负数的点都在原点的左侧．要特别注意相邻两个负整数点之间的等分点所表示的数，例如：－2，－3之间的A点是表示，而不是．

　　解：O表示0，A表示，B表示1，C表示，D表示－4，E表示－0.5．

　　例4　下面说法中错误的是 [　 ]．

　　A．数轴上原点的位置是任意取的，不一定要居中；

　　B．数轴上单位长度的大小要根据实际需要选取．1厘米长的线段可以代表1个单位长度，也可以代表2个、5个、10个、100个、…单位长度，但一经取定，就不可改动；

　　C．如果a＜b，那么在数轴上表示a的点比表示b的点距离原点更近；

　　D．所有的有理数都可以用数轴上的点表示，但不能说数轴上所有的点都表示有理数．

　　解：当a，b都是正数时，C的结论成立；

　　当a，b不都是正数时，例如a＝-10，b＝2，此时-10＜2，也满足条件a＜b，但表示a的点与原点的距离(10)比表示b的点与原点的距离(2)远，C的结论不成立．

　　∴C错．

　　说明：因为有理数包含正数、负数和0，所以用字母表示数时，这个字母就可以代表正数、负数或0．在分析问题时，忘记字母代表的数可能是负数或0经常是造成错误的原因．

　　例5 比较下列各组数的大小：

　　

　　分析：依据“正数都大于0，负数都小于0；正数大于一切负数．”和“在数轴上表示的两个数，右边的数总比左边的数大．”比较两个数的大小．

　　用通分的方法比较（5）中的两个分数的大小是很麻烦的，如果都与（中间数）比较，则可化繁为简；（6）中的两个负数，应当把小数化为分数或把分数化为小数后才便于比较．

　　解：

　　

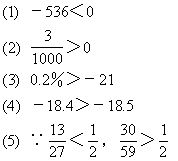
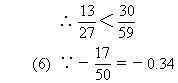
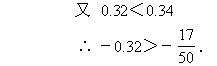
　　说明：分母不同的两个分数比较大小时，一般采用通分的方法．当分母比较大时，通分是比较麻烦的，这时应当考虑其他的方法和技巧．例如：借助中间数的方法；让分子相等比分母的方法，比较它们的倒数的方法等等．

选题角度：

　　本节从以下几个方面选题：

　　关于数轴正确画法的判定、说明数轴上给出点所对应的数、 在数轴上标出给定数的位置 、借助于数轴比较两数的大小、有关数轴概念判断的题目。

习题精选

　　一、填空题

　　1．数轴的三要素是____，____和____．

　　2．用“＞”、“＜”、“＝”连接下列各组中的两数：

　　（1）0.001______-0.001；（2）-3.14_____- ；（3） ____ ；（4）0____-0.1

　　3．在数轴上，原点左边的数都是________数，原点左边的数都是________数．

　　4．数轴上，离开原点4个单位长度的数是__________．

　　5．把-3在数轴上对应的点沿数轴移动5个单位长度后，所得的点对应的数是_________．

　　6．不小于-4，又不大于0的整数是________．

　　7．已知点 在数轴上对应的有理数为 ，将 向左移4个单位长度后，再向右移动1个单位长度得到点 ，点 对应的数为 ，则有理数 ________．

　　8．若 为有理数，在 与 之间有2001个整数，则 的取值范围是_______．

　　二、选择题

　　1．在已知的数轴上，表示-2.75的点是（　　）．

　　　　

　　A.E点　 B.F点 　C.G点 　D.H点

　　2．一个点从数轴上的原点开始，先向右移动3个单位长度，再向左移动7个单位长度，这时点所对应的数是（　　）．

　　A.3 　　B.1 　　C.-2 　　D.-4

　　3．以下四个数，分别是数轴上A.B.C.D四个点可表示的数，其中数写错的是（　　）．

　　

　

　　4．下列各语句中，错误的是（　　）．

　　A.数轴上，原点位置的确定是任意的；

　　B.数轴上，正方向可以是从原点向右，也可以是从原点向左；

　　C.数轴上，单位长度1的长度的确定， 可根据需要任意选取；

　　D.数轴上，与原点的距离等于36.8的点有两个．

　　5．用 表示的数一定是（　 ）．

　　A．负数　 B．负整数　C．正数或负数　 D．以上结论都不对

　　6．有一种记分方法：以80分为准，88分记＋8分，某个学生得分为74分，则应记为（　　 ）．

　　A．74　　 B．＋6　　C．－74　　  D．－6

　　7．给出下列四种说法：（l）自然数即是正整数；（2）正数、0、负数统称为有理数；（3）整数分为正整数和负整数；（4）非负整数和负整数组成整数集合．其中正确的说法个数为（　　 ）．

　　　A．1　　　 B．2　　　　　C．3　　 D．4

　　8．如图，根据 、 、 、 在数轴上的位置，下列关系正确的是（　　 ）．

　　　A． 　　B．

　　　C． 　　D．

　　9．若有理数 在数轴上点 表示数 ，点 表示数 ，则有（　　 ）．

　　　A．点 在点 的左边

　　B．点 在点 的右边

　　　C．点 在原点的右边，点 在原点的左边

　　D．点 和点 均在原点左边

　　10．比较 ， ， 的大小，正确的是（　　 ）．

　　　A． 　 B．

　　　C． 　 D．

　　11．若数轴上的点 对应的数是 ，那么与 相距1个单位长度的点 所对应的数是（　　 ）．

　　A． 　　B． 　 C． 或 　 D． 或

　　三、解答题

　　1．画出数轴, 在数轴上画出表示下列各数的点：

　　

　　2．在数轴上标出下列各数，并按从小到大的顺序用不等号把它们连接起来．

　　

　　3．上体育课时，老师对全班同学进行仰卧起坐测验，以能完成10次为达标，记录成绩时，超过的次数用正数表示，不足的次数用负数表示，某小组8名女生的厅局级如下：

　　＋2，＋3，－1,0，－4，＋5，－2,0

　　请在数轴上把它们表示出来，并计算该组女生的达标率．

　　4．把下列各数填入相应的集合的括号内：

　　

　　正数集合：{　　　　}；　　整数集合：{　　　　}

　　非正数集合：{　　　　}；偶数集合：{　　　　}

　　5．飞机上升用正数表示，下降用负数表示，若甲机在1500米高空，两次记录飞机飞行升降情况是＋200米，－400米；乙飞机在1400米高空，同一时间记录飞行升降情况为：＋300米，－700米，此时哪架飞机飞得高些？高多少？

　　6．用“＜”符号从小到大连接下列各数： .

　　7．为计算一个小组 16名学生数学考试的平均分，以 80分为标准，80分以上如 95分记作＋15分，若16名学生的分数顺次记作＋2，＋5，＋9，－10，－3，－6，0，－1，＋l，＋4，－3，＋4，0，＋15，＋12，－12．求这一小组16名学生的数学考试平均分．

　　8.(1)在数轴上表示出距离原点3个单位长度和4.5个单位长度的点，并用“>”号将这些点所表示的数排列起来；

　　(2)写出比-4大但不大于2的所有整数．

参考答案

　　一、1．原点，正方向，单位长度；2．（1）＞（2）＞（3）＜（4）＞；3．正、负；4． ；5． 或 ；6．0、 、 、 、；7． ；8． ．

　　二、1．D　2．D　3．B  4．B　5．D　 6．D　 7．B　 8．B 　9．B 　10．B　 11．C

　　三、1．略；2． ；3． ；

　　4．正数集合 ；整数集合 ；非正数集合 ；偶数集合

　　5．甲机高，高300米;

　　6． ；

　　7．所得正、负数相加得 ，则16名学生的平均为 ;

　　8．(1)由图看出4.5>3>-3>-4.5

　　 ：

　　(2)在数轴上画出大于-4但不大于2的数的范围．

　　

　　由图知，大于-4但不大于2的整数是：-3，-2，-1，0，1，2．