典型例题
例1 求下列各数的绝对值:
(1)-38;(2)0.15;(3)![]() ;(4)
;(4)![]() ;(5)
;(5)![]() ;(6)
;(6)![]() .
.
分析:欲求一个数的绝对值,关键是确定绝对值符号内的这个数是正数还是负数,然后根据绝对值的代数定义去掉绝对值符号,(6)题没有给出a与b的大小关系,所以要进行分类讨论.
解:(1)-38=38;(2)+0.15=0.15;
(3)∵![]() <0,∴
<0,∴![]() =-
=-![]() ;
;
(4)∵b>0,∴3b>0,3b=3b;
(5)∵![]() <2,∴
<2,∴![]() -2<0,
-2<0,![]() -2=-(
-2=-(![]() -2)=2-
-2)=2-![]() ;
;
(6)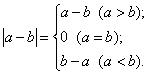
说明:分类讨论是数学中的重要思想方法之一,当绝对值符号内的数(用含字母的式子表示时)无法判断其正、负时,要化去绝对值符号,一般都要进行分类讨论.
选题角度:求数或式的绝对值。
例2 判断下列各式是否正确(正确入“T”,错误入“F”):
(1)![]() ;
( )
;
( )
(2)![]() ; ( )
; ( )
(3)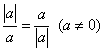 ;( )
;( )
(4)若![]() =b,则
=b,则![]() =b; ( )
=b; ( )
(5)若![]() =b,则
=b,则![]() =b; ( )
=b; ( )
(6)若![]() >b,则
>b,则![]() >b; ( )
>b; ( )
(7)若![]() >b,则
>b,则![]() >b; ( )
>b; ( )
(8)若![]() >b,则b-
>b,则b-![]() =
=![]() -b. ( )
-b. ( )
分析:判断上述各小题正确与否的依据是绝对值的定义,所以思维应集中到用绝对值的定义来判断每一个结论的正确性.判数(或证明)一个结论是错误的,只要能举出反例即可.如第(2)小题中取![]() =1,则-
=1,则-![]() =-1=-1,而-
=-1=-1,而-![]() =-1=1,所以-
=-1=1,所以-![]() ≠-
≠-![]() .同理,在第(6)小题中取
.同理,在第(6)小题中取![]() =-1,b=0,在第(4)、(7)小题中取
=-1,b=0,在第(4)、(7)小题中取![]() =5,b=-5等,都可以充分说明结论是错误的.要证明一个结论正确,须写出证明过程.如第(3)小题是正确的.证明步骤如下:
=5,b=-5等,都可以充分说明结论是错误的.要证明一个结论正确,须写出证明过程.如第(3)小题是正确的.证明步骤如下:
当![]() 时,
时,![]() ,而
,而![]() ,
,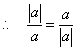 成立;
成立;
当![]() 时,
时,![]() ,而
,而![]() ,
,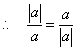 也成立.
也成立.
这说明![]() 时,总有成立.此题证明的依据是利用的定义,化去绝对值符号即可.对于证明第(1)、(5)、(8)小题要注意字母取零的情况.
时,总有成立.此题证明的依据是利用的定义,化去绝对值符号即可.对于证明第(1)、(5)、(8)小题要注意字母取零的情况.
解:其中第(2)、(4)、(6)、(7)小题不正确,(1)、(3)、(5)、(8)小题是正确的.
说明:判断一个结论是正确的与证明它是正确的是相同的思维过程,只是在证明时需要写明道理和依据,步骤都要较为严格、规范.而判断一个结论是错误的,可依据概念、性质等知识,用推理的方法来否定这个结论,也可以用举反例的方法,后者有时更为简便.
选题角度:根据绝对值的定义,判断结论是否正确。
例3 比较下列几组数的大小.
(1)![]() 和
和![]() (2)
(2)![]() 和
和![]() (3)
(3)![]() 和2.
和2.
分析:(1)中是两个负数的比较,可先比较它们的绝对值,绝对值大的反而小;(2)中是两个负数的绝对值的比较,应先求出绝对值,直接进行比较;(3)中是一负数与一正数的比较,正数大小一切负数.
解:(1)∵![]()
![]() ,又∵
,又∵![]() ,∴
,∴![]() .
.
(2)∵![]() ,
,![]() ,又∵
,又∵![]() ,∴
,∴![]() .
.
(3)∵![]() ,
,![]() ,∴
,∴![]() .
.
说明:解答此类题应注意以下几点:(1)两负数比较时,采用比较绝对值的方法;(2)两数的绝对值比较则应先求绝对值,再直接比较;(3)根据正数的意义,正数大于一切负数.
选题角度:比较有理数的大小。
习题精选
一、填空题
1.![]() 中最大的一个数是________,最小的一个数是________.
中最大的一个数是________,最小的一个数是________.
2. 有理数![]() ,
,![]() 在数轴上的位置如图,比较大小:
在数轴上的位置如图,比较大小:![]() ________
________![]() ,
,![]() ________
________![]() .
.
![]()
3. 若![]() -1 =0, 则
-1 =0, 则![]() =________,若1-
=________,若1-![]() =1,则
=1,则![]() =________.
=________.
4.把四个数![]() 和
和![]() 用“<”号连接起来是________________________.
用“<”号连接起来是________________________.
5.一个数的倒数是它本身,这个数是________,一个数的相反数是它本身,这个数是________.
6.若![]() 的相反数是5,则
的相反数是5,则![]() 的值为________.
的值为________.
7.一个数比它的绝对值小10,则这个数为________.
8.若![]() ,
,![]() ,
,![]() ,则
,则![]() 与
与![]() 的大小关系是________.
的大小关系是________.
9.若![]() ,且
,且![]() ,则
,则![]() ________.
________.
二、选择题
1.比较三个数![]() 的大小,下列各式中正确的是( ).
的大小,下列各式中正确的是( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2. 如果![]() >0,
>0,![]() <0,
<0,
![]() <
<![]() ,那么
,那么![]() ,
,![]() ,-
,-![]() , -
, -![]() 的大小关系
( ).
的大小关系
( ).
A.-![]() >
>![]() >-
>-![]() >
>![]() B.
B.![]() >
>![]() >-
>-![]() >-
>-![]()
C.-![]() >
>![]() >
>![]() >-
>-![]() D.
D.![]() >
>![]() >-
>-![]() >-
>-![]()
3.一个数在数轴上所对应的点向右移动5个单位长度后,得到它的相反数的对应点,则这个数应是( ).
A.![]() B.2 C.
B.2 C.![]() D.
D.![]()
4.一个数在数轴上的对应点与它的相反数在数轴上的对应点的距离为![]() 个单位长度,则这个数是( ).
个单位长度,则这个数是( ).
A.![]() 或
或![]() B.
B.![]() 或
或![]()
C.![]() 或
或
![]() D.
D.![]() 或
或![]()
5.一个数在数轴上对应点到原点距离为![]() ,则这个数的绝对值为( ).
,则这个数的绝对值为( ).
A.![]() B .
B .![]() C.
C.![]() D.
D. ![]()
6.已知![]() ,
,![]() ,且
,且![]() ,则( ).
,则( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.数![]() ,
,![]() ,
,![]() 的绝对值的大小关系是( ).
的绝对值的大小关系是( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.若![]() ,则( ).
,则( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.在数轴上,下面说法中不正确的是( ).
A.两个有理数,绝对值小的离原点近
B.两个有理数,大数对应的点在右边
C.两个负数,较大的数对应的点离原点近
D.两个有理数,大的离原点较远
10.![]() 、
、![]() 、
、![]() 、
、![]() 都是有理数,且
都是有理数,且![]() ,
,![]() ,那么
,那么![]() 与
与![]() ( ).
( ).
A.互为相反数 B.互为倒数 C.互为负倒数 D.相等
三、解答题
1.已知![]() 、
、![]() 、
、![]() 的位置如图,试化简
的位置如图,试化简![]() .
.
![]()
2.已知![]() ,
,![]() ,且
,且![]() ,试求
,试求![]() ,
,![]() 的值.
的值.
3.比较下列各数的大小:(1)![]() 和
和![]() ;(2)
;(2)![]() ,
,![]() 和
和![]() .
.
4.若![]() ,且数轴上表示
,且数轴上表示![]() 的点到原点的距离大于表示
的点到原点的距离大于表示![]() 的点到原点的距离,试把
的点到原点的距离,试把![]() ,
,![]() ,
,![]() ,
,![]() 这四个数从大到小排列起来.
这四个数从大到小排列起来.
5.若![]() ,试求
,试求![]() 的值.
的值.
6.把![]() 记在数轴上,并按从小到大的顺序排列出来.
记在数轴上,并按从小到大的顺序排列出来.
7.计算:![]()
8.已知![]() 、
、![]() 、
、![]() 、
、![]() 为有理数,其中
为有理数,其中![]() 、
、![]() 、
、![]() 在数轴上的位置,如图所示,且
在数轴上的位置,如图所示,且![]() ,求
,求![]() 的值.
的值.
![]()
参考答案
一、1.![]() ;2. >,>;3. 1,0或-2;4.
;2. >,>;3. 1,0或-2;4. ![]() ;
;
5.![]() ,0;6.
,0;6.![]() ;7.
;7.![]() ;8.
;8.![]() ;9.
;9.![]() .
.
二、1. A 2. A 3.D 4.B 5.B 6.B 7.B 8.D 9.D 10.A
三、1.![]() ;
;
2.![]() ,
,![]() 或
或![]() ,
,![]() ;
;
3.(l)![]() ;(2)
;(2)![]() ;
;
4.![]() ;
;
5.∵![]() ,
,![]() ∴
∴![]() ,
,![]() ∴
∴![]() ;
;
6.![]() ;
;
7.原式![]()
8.观察可得![]() ,由已知条件可求得:
,由已知条件可求得:![]() ,
,![]() ,
,![]() ,
,![]() ,故原式
,故原式![]() .
.