典型例题

　　例1　计算

　　（1）（－9）＋（－8）；（2） ；

　　（3） ；（4） ．

　　分析：在有理数加法运算时，应注意包括符号确定和绝对值运算两部分．绝对值计算是小学数学中的计算，而符号又分为同号两数与异号两数两种情况．因此计算时应先确定和的符号，再计算它们的绝对值．

　　解：（1）（－9）＋（－8）＝－（－9＋－8）＝－17；

　　　　（2） ；

　　　　（3） ；

　　　　（4） ．

　　说明：①注意特殊情况：一个数与0相加仍得这个数；互为相反数的两个数相加得0；

　　　　　②第（2）题的结果中“ ”要注意约分．

　　选题角度：关于两个有理数相加的题目

　　例2　计算 ．

　　分析： 做带分数加法时，可将整数部分与分数部分相加，然后再把结果相加；

　　解：

　　

　　

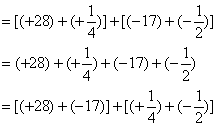
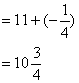
　　说明：解题时要注意：①分开的整数部分与分数部分必须保持原带分数的符号．②运算符号和数的性质符号要用括号分开，如： ，这里的“+”是运算符号，“－”是性质符号，这两个符号不能连在一起写成“ ”．

　　选题角度：关于两个真分数相加的题目

　　例3　计算：

　　（1）16.96＋(－3.8)＋5.2＋(－0.2)＋(－0.96)；

　　（2） ．

　　分析：(1)中16.96＋(－0.96)和(－3.8)＋(－0.2)都是整数，应当先做加法；(2)中分母为37的分数分布在两个中括号里，应当先去掉中括号，运用加法的交换律和结合律，把分母为37的分数结合起来运算，才能使计算简便．

　　解：(1)原式＝[16.96 ＋ (－0.96)] ＋ [(－3.8) ＋ (－0.2)] ＋5.2

　　　　　　　 ＝16＋(－4)＋5.2

　　　　　　　 ＝17.2．

　　(2)原式

　　　　　

　　　　　

　　　　　

　　说明：学会观察是此例训练的目的，对于较为复杂的题，先观察分析，发现加数间的联系，而后再选择一个最佳方案，是解决问题的一般思路．在数学的学习中，有意识地培养这种能力是非常重要的，多个有理数相加时，应灵活运用加法运算律，适当交换各个加数的位置，遇到分数，先把同分母的分数结合；遇到小数，先把相加得整数的小数结合．这样能使计算简便些．

　　选题角度：关于多个有理数相加的题目

　　例4　计算下列各式：

　　（1）

　　（2）

　　分析：可仿上题用分组结合法来解之．

　　解：（1）原式

　　　　　　　　

　　（2）原式

　　　　　　

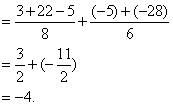
　　说明：对分式的计算，应从分母出发考虑分组，即将分母可化为相同的分成一组，以便于进行计算．

　　选题角度：关于分数求和的题目

习题精选

　　一、选择题

　　1．两个有理数的和的绝对值与它的绝对值的和相等，则（　 ）．

　　（A）这两个有理数都是正数

　　（B）这两个有理数都是负数

　　（C）这两个有理数同号

　　（D）这两个有理数同号或至少一个为零　

　　2．若 ，则以下式子中一定成立的是（　 ）．

　　（A）　　　　　（B） 　

　　（C）　　（D）

　　3．使 成立的x是 （　 ）．

　　（A）任意一个数　　（B）任意一个大于-2000的数

　　（C）任意一个负数　（D）任意一个非负数

　　4．下列各式计算结果等于 的是（　　）．

　　（A） 　　（B）

　　（C） 　　　（D）

　　5．如果两个有理数的和是正数，那么一定是（　　）．

　　（A）这两个数都是正数

　　（B）一个数是正数，另一个数是零

　　（C）一为正数、一为负数，且正数的绝对值较大

　　（D）属于以上三种情况之一

　　6．甲、乙两数的和与甲数比较，其大小关于是（　　）．

　　（A）和必大于甲数　　　　（B）和必小于甲数

　　（C）和必不小于甲数　　　（D）由乙数的取值情况

　　二、填空题

　　1．（1） 　　（2）

　　（3） 　　　（4）

　　（5） 　　 （6）

　　2．已知有理数a、b、c在数轴上对应点如图所示，且

　　

　　（1） 　 （2）

　　（3） 　（4） ．

　　3．a、b为有理数，从 ， ， 中选出一个或几个适当的式子填空，使下列说法正确．

　　（1）因为_______，所以a、b都不为零．

　　（2）因为________，所以a、b至少有一个为正数．

　　（3）因为a、b都为零，所以_________．

　　（4）因为a、b都不为零，所以___________．

　　（5）因为a、b不都为零，所以___________．

　　三、判断题“对”的填入T，“错”的填入F．

　　1．两个有理数的和为正数时，这两个数都是正数． ( 　 )

　　2．两个数的和的绝对值一定等于这两个数绝对值的和． ( 　 )

　　3．两个有理数的和为负数时，这两个数都是负数． (　  )

　　4．如果两个数的和为负数，那么这两个加数中至少有一个是负数． (　  )

　　5．两数之和必大于任何一个加数． ( 　 )

　　6．如果两个有理数的和比其中任何一个加数都大,那么这两个数都是正数． ( 　 )

　　7．两个不相等的有理数相加，和一定不等于0． (　  )

　　8．两个有理数的和可能等于其中一个加数． ( 　 )

　　四、解答题

　　1．计算：

　　（1） (－7.3)＋(－2) 　　　　（2）－2.1＋(－1.9)

　　（3）(＋1.75)＋(－8.35)　　　（4）

　　2． 计算：

　　（1） （2） ,

　　（3） （4） ．

　　3．计算题

　　（1） ；

　　（2） ；

　　（3） ；

　　（4） ；

　　（5） ；

　　（6） ．

　　 4．用简便方法计算

　　（1） ；

　　（2） ．

　　5．求 的绝对值的相反数与 的相反数的倒数之和．

　　6．求使下列各式成立的 值．

　　（1） ；（2） ；

　　（3） ；（4） ．

　　7．求绝对值小于2003的所有整数之和．

　　8．已知： ， ， ， ，求 的值．

　　9．已知： ， ，求 的值．

参考答案

　　一、1．D　 2．D　 3．D　4．A　5．D　6．D

　　二、1．（1）0；（2）0；（3）32；（4）16；（5）22；（6）10

　　2．（1） ；（2）；（3）；（4）

　　3．（1） ，；（2）；（3）；

　　　（4）（5）

　　三、1．F．异号两数相加，当正数的绝对值较大时，和就是正数．

　　2．F．异号两数相加时，和的绝对值等于这两数绝对值之差．

　　3．F．异号两数相加时，若负数的绝对值较大，则和为负数．

　　4．T．

　　5．F．当两个加数中有一个负数或0时，它们的和必小于或等于另一个加数．

　　6．T．

　　7．F．两个互为相反数的数之和等于0．

　　8．T．任何一个有理数与0的和就等于它本身．

　　四、1．(1) －9.3 ； 　(2) 0.2 ；　　(3)  －6.6；　 （4）0．

　　2．（1） ； （2） ；　（3）－149.95； （4） ．

　　3．（1） ；（2）20；（3）－7；（4）－510；（5） （6） ．

　　4．（1） ，（2）－34．

　　5． ．

　　6．（1） ；（2） ；（3） ；（4） ．

　　7．0．

　　8． ．

　　9． ； ．