北师大版七年级数学(下)第一章《整式的运算》测试题
班别:________ 姓名:________ 座号:________ 成绩:__________
一、填空(3′×9)
1、3-2=________;
2、有一单项式的系数是2,次数为3,这个单项式可能是________;
3、________÷a=a3;
4、一种电子计算机每秒可做108次计算,用科学记数法表示它8分钟可做___________次运算;
5、一个十位数字是a,个位数学是b的两位数表示为10a+b,交换这个两位数的十位数字和个位数字,又得一个新的两位数,它是________,这两个数的差是________;
6、有一道计算题:(-a4)2,李老师发现全班有以下四种解法,
①(-a4)2=(-a4)(-a4)=a4·a4=a8;
②(-a4)2=-a4×2=-a8;
③(-a4)2=(-a)4×2=(-a)8=a8;
④(-a4)2=(-1×a4)2=(-1)2·(a4)2=a8;
你认为其中完全正确的是(填序号)_______;
7、我国北宋时期数学家贾宪在他的著作《开方作法本源》中的“开方作法本源图”如下图⑴所示,通过观察你认为图中a=________;
8、有二张长方形的纸片(如图⑵),把它们叠合成图⑶的形状,这时图形的面积是_____________;

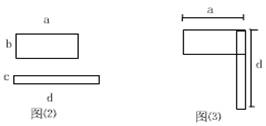
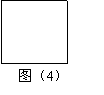
9、小华把一张边长是a厘米的正方形纸片(如图⑷)的边长减少1厘米后,重新得到一个正方形纸片,这时纸片的面积是_____________厘米;
二、选择题(3′×3)
 10、下列运算正确的是( )
10、下列运算正确的是( )
A.a5·a5=a25 B.a5+a5=a10
C .a5·a5=a10 D.a5·a3=a15
11、计算 (-2a2)2的结果是( )
A 2a4 B -2a4 C 4a4 D -4a4
12、用小数表示3×10-2的结果为( )
A -0.03 B -0.003 C 0.03 D 0.003
三、计算下列各题(8′×5)
13、(2a+1)2-(2a+1)(-1+2a) 14、(3xy2)·(-2xy)
15、(2a6x3-9ax5)÷(3ax3) 16、(-8a4b5c÷4ab5)·(3a3b2)
17、(x-2)(x+2)-(x+1)(x-3)
四、(6′)七年级学生小颖是一个非常喜欢思考问题而又乐于助人的同学,一天邻居家正在读小学的小明,请小颖姐姐帮忙检查作业:
7×9= 63 8×8=64
11×13=143 12×12=144
24×26=624 25×25=625
小颖仔细检查后,夸小明聪明仔细,作业全对了!小颖还从这几道题发现了一个规律。你知道小颖发现了什么规律吗?请用字母表示这一规律,并说明它的正确性。
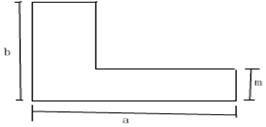
五、(7′)古人云:凡事宜先预后立。我们做任何事都要先想清楚,然后再动手去做,才可能避免盲目性。一天,需要小华计算一个L形的花坛的面积,在动手测量前小明依花坛形状画了如下示意图,并用字母表示了将要测量的边长(如图所标示),小明在列式进行面积计算时,发现还需要再测量一条边的长度,你认为他还需测哪条边的长度?请你在图中标示出来,并用字母n表示,然后再求出它的面积。
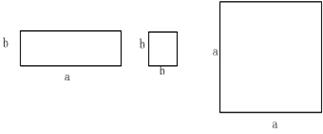
六、(6′)如图所示的长方形或正方形三类卡片各有若干张,请你用这些卡片,拼成一个长方形或正方形图形。
要求:所拼图形中每类卡片都要有,卡片之间不能重叠。
画出示意图,并计算出它的面积。
七、(7′)小华看着电视里的舞蹈节目:七个身穿不同民族服装的舞蹈演员正在面对观众进行队列变换,他陷入了沉思:这7个演员面对观众一共会有几种队列变换呢?……为了解决这一问题,他是这样思考和探索的:
①若只有一个演员A,那就只有队列变换A,共1种;
②若有二个演员A、B,那就有队列变换:AB和BA,共2种;
③若有三个演员A、B、C,那就有队列变换:ABC、ACB、BAC、BCA、CAB、CBA,共6种;
④若有四个演员A、B、C、D,那就有队列变换(小华把这四个字母在纸上不停的变换顺序地排列着、写着)……数数看,哇!有24种,变化如此之快呀,五个、六个、七个演员呢?看来不可再强攻,否则就……,还是智取吧……
再应用表格吧,记得书上有这样的例子,老师也曾示范过,它能更加清楚地反映其中的数字规律呢:
| 演员的个数_ | 1_ | 2_ | 3_ | 4_ | ……_ |
| 可能有的变换数_ | 1_ | 2_ | 6_ | 24_ | ……_ |
……
⑴你知道这7个舞蹈演员面对观众一共会有几种队列变换吗?说说你的理由。
⑵请你先仔细体会小华的解题策略,然后再探索:220的末位数字是多少?说说你是怎样想的。例如:25的末位数字是5;2043的末位数字是3。