典型例题
例1 计算:![]() .
.
分析:此算式以加、减分段, 应分为三段:![]() ,
, ![]() ,
, ![]() .这三段可以同时进行计算,先算乘方,再算乘除.式中-0.2化为
.这三段可以同时进行计算,先算乘方,再算乘除.式中-0.2化为![]() 参加计算较为方便.
参加计算较为方便.
解:原式![]()
![]()
![]()
![]()
说明:做有理数混合运算时,如果算式中不含有中括号、大括号,那么计算时一般用“加”、“减”号分段,使每段只含二、三级运算,这样各段可同时进行计算,有利于提高计算的速度和正确率.
例2 计算:![]() .
.
分析:此题运算顺序是:第一步计算 ![]() 和
和
![]() ;第二步做乘法;第三步做乘方运算;第四步做除法.
;第二步做乘法;第三步做乘方运算;第四步做除法.
解:原式 ![]()
![]()
![]()
![]()
![]()
![]()
说明:由此例题可以看出,括号在确定运算顺序上的作用,所以计算题也需认真审题.
例3 计算:![]()
![]()
分析:要求![]() 、
、![]() 、
、![]() 的值,用笔算在短时间内是不可能的,必须另辟途径.观察题目发现,
的值,用笔算在短时间内是不可能的,必须另辟途径.观察题目发现,![]() ,
,![]() ,逆用乘法分配律,前三项可以凑成含有0的乘法运算,此题即可求出.
,逆用乘法分配律,前三项可以凑成含有0的乘法运算,此题即可求出.
解:原式 ![]()
![]()
![]()
![]()
![]()
说明:“0”乘以任何数等于0.因为运用这一结论必能简化数的计算,所以运算中,能够凑成含“0”因数时,一般都凑成含有0的因数进行计算.当算式中的数字很大或很繁杂时,要注意使用这种“凑0法”.
例4 计算![]()
![]()
分析: ![]() 是
是![]() 的倒数,应当先把它化成分数后再求倒数;右边两项含绝对值号,应当先计算出绝对值的算式的结果再求绝对值.
的倒数,应当先把它化成分数后再求倒数;右边两项含绝对值号,应当先计算出绝对值的算式的结果再求绝对值.
解:原式 ![]()
![]()
![]()
![]()
![]()
说明:对于有理数的混合运算,一定要按运算顺序进行运算,注意不要跳步,每一步的运算结果都应在算式中体现出来,此题(1)要注意区别小括号与绝对值的运算;(2)要熟练掌握乘方运算,注意(-0.1)3,-0.22,(-2)3,-32在意义上的不同.
例5 计算: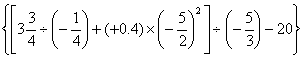
![]() .
.
分析:含有括号的混合运算,一般按小、中、大括号的顺序进行运算,括号里面仍然是先进行第三级运算,再进行第二级运算,最后进行第一级运算.
解:原式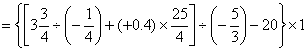
![]()
![]()
![]()
例6 计算![]()
解法一:原式![]()
![]()
解法二:原式![]()
![]()
![]()
说明:加减混合运算时,带分数可以化为假分数,也可把带分数的整数部分与分数部分分别加减,这是因为带分数是一个整数和一个分数的和.
例如:![]()
习题精选
一、选择题
1.若![]() ,
,![]() ,则有( ) .
,则有( ) .
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() 的值是( ) .
的值是( ) .
A.![]() B.44C.28 D.17
B.44C.28 D.17
3.如果![]() ,那么
,那么![]() 的值为( ) .
的值为( ) .
A.0B.4C.-4D.2
4.代数式![]() 取最小值时,
取最小值时,![]() 值为( ) .
值为( ) .
A.![]() B.
B.![]() C.
C.![]() D.无法确定
D.无法确定
5.六个整数的积![]() ,
,![]() 互不相等,则
互不相等,则![]() ( ) .
( ) .
A.0 B.4C.6D.8
6.计算![]() 所得结果为( ) .
所得结果为( ) .
A.2B.![]() C.
C.![]() D.
D.![]()
二、填空题
1.有理数混合运算的顺序是__________________________.
2.已知![]() 为有理数,则
为有理数,则![]() _________0,
_________0,![]() _________0,
_________0,![]() _______0.(填“>”、“<”或“≥”=)
_______0.(填“>”、“<”或“≥”=)
3.平方得16的有理数是_________,_________的立方等于-8.
4.![]() __________.
__________.
5.一个负数减去它的相反数后,再除以这个负数的绝对值,所得商为__________.
三、判断题
1.若![]() 为任意有理数,则
为任意有理数,则![]() .( )
.( )
2.![]()
![]() .( )
.( )
3.![]() .( )
.( )
4.![]() .()
.()
5.![]()
![]() .( )
.( )
四、解答题
1.计算下列各题:
(1)![]() ;
;
(2)![]() ;
;
(3)![]() ;
;
(4)![]() ;
;
(5)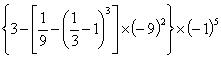 ;
;
(6)![]()
![]() ;
;
(7)![]() ;
;
(8)![]() .
.
2.若有理数![]() 、
、![]() 、
、![]() 满足等式
满足等式![]()
![]() ,试求
,试求![]() 的值.
的值.
3.当![]() ,
,![]() 时,求代数式
时,求代数式![]()
![]() 的值.
的值.
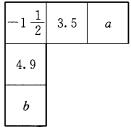
4.已知如图2-11-1,横行和竖列的和相等,试求![]() 的值.
的值.
5.求![]() 的值.
的值.
6.计算![]() .
.
参考答案:
一、1.C 2.C 3.C 4.B 5.A 6.B
二、1.略;2.≥,>,<;3.![]() ,
,![]() ;4.1;5.
;4.1;5.![]() .
.
三、1.× 2.× 3.√ 4.× 5.√
四、1.(1)![]() (2)
(2)![]() (3)
(3)![]() (4)
(4)![]() (5)30(6)
(5)30(6)![]() (7)
(7)![]() (8)
(8)![]() ; 2.∵
; 2.∵![]() ,
,![]() ,
,![]() ∴
∴![]() ;
;
3.![]() ;
;
4.![]() ,
,![]() ,
,![]() ;
;
5.设![]() ,则
,则![]() ,
,![]() ;
;
6.原式![]() .
.