填空题

　　1．某商品原价 元，若八六折出售，现在的售价是_________．

　　2．一个生产车间共生产 个零件，原计划每天生产 个零件，如果每天多生产5个零件，可以提前_________天完成．

　　3．某商品价格为 元，降价10％后，又降价10％，结果销售额猛增．最后商店决定再提价20％，则提价后这种商品的价格为_________．

　　4．在 千克盐水中，盐与水之比为 ，则其中含盐_________千克．

　　5． 、 、5三数的平均值为_________，三数的积为_________．

　　6．若 为自然数，则被4除余1的数可表示为_________，被7除余3的数可表示为_________．

　　7．甲、乙两仓库共有货物 吨，其中甲仓库比乙仓库多5吨；则甲仓库有货物_________吨．

　　8．除以 的商是 ，余数是 的数是_________．

　　9． 个人 天做完的工作，若增加 个人，则可提前_________天完成这项工作．

　　10．三个连续奇数，中间一个是 ，则这三个数的和的平方是_________．

　　11．一个三位数，十位上的数字是 ，个位上的数字比十位上的数字小2，百位上的数字是个位上的数与十位上的数的平均数，则这个三位数可表示为_________．

　　12．已知下列一组数：1， ， ， ， ，…用代数式表示第 个数为_________．

　　参考答案：

　　1．① 元　2． 天　3． 　　4．   5． 　　 6． 　　 7． 8．   9．   10．   11．   12．

 选择题

　　1．用代数式表示： 除 的商与3的倒数的和是（　 ）．

　　（A） 　　（B） 　　（C） 　　（D）

　　2．被8除商 余5的数是（　 ）．

　　（A） 　 （B） 　　（C） 　（D）

　　3．用代数式表示与 的和是8的数是（　　 ）

　　A． 　 B． 　 C． 　 D．

　　4．设甲数为 ，它比乙数的倒数小7，则乙数为（　　 ）．

　　A． 　　B． 　 C． 　 D．

　　5．A、B两地相距 千米，甲每小时行 千米，乙的速度是甲的1.2倍，甲乙两人分别从A、B两地同时出发，相向而行，他们相遇时所行走的时间是（　　 ）．

　　A． 小时　　B． 小时　　C． 小时　 D． 小时

　　6．小明到书店买了 本书，比小红买的书多 ，则小红买书的本数是（　　 ）．

　　A． 　　B． 　 C． 　 D．

　　7．下列各判断中，所列代数式错误的是（　　 ）．

　　A．表示“比 与 的积的 2倍小5的数”是

　　B．表示“ 、 两数的平方差的倒数”是

　　C．表示“甲数为 ，乙数为 ，甲、乙两数的和与它们的积的差”是

　　D．表示“数 的一半与数 的3倍的差”是

参考答案

　　1．C  2．A　　3．C　 4．B　 5．A　 6．B　 7．B

重难点分析

　　列代数式实质是实现从基本数量关系的语言表述到代数式的一种转化。列代数式首先要弄清语句中各种数量的意义及其相互关系，然后把各种数量用适当的字母来表示，最后再把数及字母用适当的运算符号连接起来，从而列出代数式。

　　如：用代数式表示：比 的2倍大2的数。

　　分析  本题属于“…比…多（大）…或…比…少（小）”的类型，首先要抓住这几个关键词。然后从中找出谁是大数，谁是小数，谁是差。比 的2倍大2的数换个方式叙述为所求的数比 的2倍大2。大和比前边的量，即所求的数为大数，那么比和大之间量，即 的2倍则为小数，大后边的量2即为差。所以本小题是已知小数和差求大数。因为大数=小数+差，所以所求的数为：2 +2.

 解答题

　　1．用代数式表示：

　　（1）与 的和是30的数；　　（2）与 的差是 的数；

　　（3）与 的积是15的数；　 （4）与 的商是 的数；

　　（5）被4整除商 的数；　　　 （6）被4除商 余3的数。

　　2．某校组织学生参加公益劳动，初二年级有 人报名，初一年级比初二年级报名人数多10％，初三年级比初二年级报名人数少 ．求该校每个年级报名参加公益劳动的平均人数．

　　3．甲、乙二人从同一地点出发，甲每小时走 千米，乙每小时走 千米 ．用代数式表示：

　　（1）反向行走 小时，两人相距多少千米？

　　（2）同向行走 小时，两人相距多少千米？

　　4．某工厂一月份产值是 万元，二月份比一月份增长 ，三月份又比二月份增长 ，用代数式表示三月份的产值．

　　5．一项工程，甲队单独完成需用 天，乙队单独完成需用 天，若两队合作，完成这项工程共需多少天？

　　6．要制造 个零件，原计划每天造 个，用代数式表示制造完这批零件需用多少天；若每天比原计划多制造20个零件，用代数式表示可以提前几天完成．

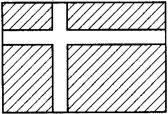
　　7．如图l-2-1，为了绿化校园，学校决定修建一块长方形草坪，且长30米，宽20米，并在草坪上修建如图所示的十字路，小路宽 米，用代数式表示：

　　（1）修建的小路面积为多少平方米？（2）草坪面积是多少平方米？（△）

　

　　8．用代数式表示下列问题的答案：甲乙两人从同一地点出发，甲每小时走 千米，乙每小时走 千米（ ），用代数式表示：（1）反向行走 小时，两人相距多少千米？（2）同向行走对 小时，两人相距多少千米？（3）反向行走，甲比乙早出发 小时，乙走 小时，两人相距多少千米？（4）同向行走，甲比乙晚出发 小时，乙走 小时（ ），两人相距多少千米？

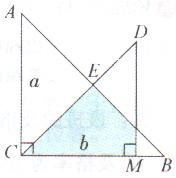
　　9．如右图，三角形ABC和三角形DCM都是等腰直角三角形。AC的长为 ，CM的长为 （ ），请用代数式表示图中阴影部分的面积。

　　10．任意选择小于10的三个不同的数，从这三个数中任取两个构成两位数，可以得到六个不同的两位数；用这六个两位数相加的和除以这三个不同的数的和，所得的商是22．请你说明这个结论的正确性．

　　参考答案

　　1．（1） ；　（2） ；（3） ；　 （4） ．

　　2． ．

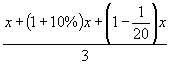　　3．（1）反向而行， 小时后两人之间的距离即为两人所走路程之和，得 千米（或 千米）．

　　　　  （2）同向而行， 小时后两人之间的距离即为两人所走路程之差，得 千米（或 千米）．

　　4．二月份的产值是 万元；三月份的产值是 万元．也就是　　　　　　　　　  万元．

　　5．由题意，甲、乙两队合做，一天能完成工程的 ，那么完成整个工程所需的天数是 天，即为 天．

　　6．要制造 个零件，每天制造 个，则需用 天完成；如果每天比原计划多制造20个零件，可以提前 天完成．

　　7．（1） 　（2） ．

　　8．（1） 千米　（2） 千米　（3） 千米　 （4） 千米； 千米或0．

　　9． ．

　　10．用 、 、 表示任意三个不同的小于10的数，从中任取两个可构成以下六个两位数： ， ， ， ， ， ．

　　设这六个两位数的和为 ，则

　　

　　 ∴

　　即所得结论是正确的．

注意问题

　　1、要分清语言叙述中关键词语的意义，理清它们之间的数量关系。如要注意题中的“大”，“小”，“增加”，“减少”，“倍”，“倒数”，“几分之几”等词语与代数式中的加，减，乘，除的运算间的关系。

　　2、弄清运算顺序和括号的使用。一般按“先读先写”的原则列代数式。

　　3、数字与字母相乘时数字写在前面，乘号省略不写，字母与字母相乘时乘号省略不写。

　　4、在代数式中出现除法时，用分数线表示。