平行线与相交线复习
2.1 台球桌面上的角
(1) 余角--------如果两个角的和是直角,那么称这两个角互为余角。
(2) 补角--------如果两个角的和是平角,那么称这两个角互为补角。
(3) 对顶角------两条相交直线中,有公共顶点,它们的两边互为反向延长线的两个角叫做对顶角.(对顶角相等)
例:如右图1 互为余角的有__________________________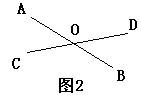 互为补角的有___________________图中有对顶角吗? 答:____________
互为补角的有___________________图中有对顶角吗? 答:____________
 |  | ||
如右图2 对顶角有_______对.它们分别是____________
2 探索直线平行的条件
(1) 同位角,内错角,同旁内角。常见的图形如图3。
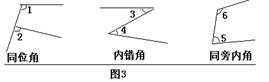
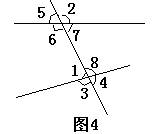
例:找出图4中的同位角,内错角,同旁内角:
同位角有_______________________________
内错角有_______________________________
同旁内角有_____________________________
(2)两直线平行的判定:
同位角____________,两直线平行。
 内错角____________,两直线平行。
内错角____________,两直线平行。
同旁内角__________,两直线平行。
例:如图5,
由∠1=∠3得___ //____( )
由∠2=∠3 得___ //____( )
由∠3+∠4=180
得___ // ____( )
由∠2+∠4=180°
得___ // ____( )
2.3 平行线的特征:
两直线平行,同位角___________
两直线平行,内错角____________.
两直线平行,同旁内角____________.
2.4 用尺规作线段和角
二 巩固练习
一 填空:
(1)∠A的余角是20°,那么∠A等于________度.
(2)∠A与∠B互补,如果∠A=36°,那么∠B的度数为_________.
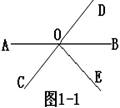
(3)如图1-1所示,∠AOC=36,∠DOE=90,
则∠BOE=_______.
(4)如图1-1中,有_________对对顶角.
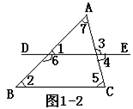
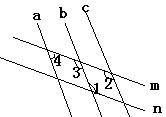
(5)如图1-2中,已知四条直线AB,BC,CD,DE。
问:①∠1=∠2是直线______和直线______被直线_____所截而成的____角. ②∠1=∠3是直线_____和直线_____被直线_____所截而成的____角.
③∠4=∠5是直线______和直线______被直线_____所截而成的____角.
④∠2=∠5是直线______和直线______被直线_____所截而成的____角.
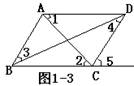
(6)如图1-3:
①∵∠1=∠2,∴_____∥_____,理由是________________.
②∵AB∥DC,∴∠3=∠_______,理由是_________________.
③∵AD∥______,∴∠5=∠ADC,理由是__________________.
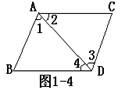
(7)如图1-4所示:
①如果∠1=∠3,可以推出______∥_______,其理由是________________②如果∠2=∠4,可以推出______∥_______,其理由是__________________
③如果∠B+∠BAD=180°,可以推出____∥____,其理由是________________
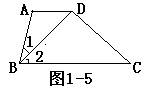
(8)如图1-5,已知AD//BC,∠1=∠2,∠A=112°,且BD⊥CD,则∠ABC=_____,∠C=_____.
二 选择题.
(1) 若∠1与∠2的关系为内错角,∠1=40°,则∠2等于( )
A. 40° B. 140° C. 40°或140° D. 不确定
(2) 下列说法正确的是( )
A. 若两个角相等,则这两个角是对顶角.
B. 若两个角是对顶角,则这两个角是相等.
C. 若两个角不是对顶角,则这两个角不相等.
D. 所有的对顶角相等
(3) 下列说法正确的是( )
A. 有公共顶点,并且相等的两个角是对顶角
B. 两个角的两边分别在同一条直线的,这两个角互为对顶角
C. 如果两个角不相等,那么这两角不是对顶角
D. 如果两个角相等,那么这两个角是对顶角
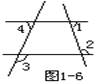
(4) 如图1-6,∠1和∠2互补,∠3=130°,那么∠4的度数是( )
A. 50° B. 60° C.70° D.80°
(图1-10)
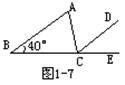
(5) 如图1-7,已知B、C、E在同一直线上,且CD//AB,若∠A=105°,∠B=40°,则∠ACE为( )
A.35° B. 40° C. 105° D. 145°
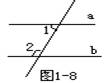
(6) 如图1-8 , a // b,,且∠2是∠1的2倍,那么∠2等于( )
A. 60° B. 90° C. 120° D. 150°
(7) 如图1-9 ,AB,CD交于点O,OE⊥AB于O,则下列说法中不正确的是( )
A.∠1与∠2是对顶角 B. ∠2与∠3是互为余角
C. ∠1和∠3是互为余角 D. ∠3和∠4是对顶角
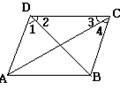
(8) 如图1-10 , 若∠1+∠2+∠3+∠4=180°,则( ) A.AD // BC B. AB // CD
C. BD⊥DC D. AB⊥BC
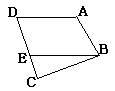
三 解答题: 如右图,AB //CD ,AD // BE ,试说明
∠ABE=∠D.
∵ AB∥CD (已知)
∴ ∠ABE=___________(两直线平行,内错角相等)
 ∵ AD∥BE (已知)
∵ AD∥BE (已知)
∴ ∠D=_________ ( )
∴∠ABE=∠D ( 等量代换)