|
A卷（满分100分）
一、填空题（每空1分，共22分）
1、单项式
的系数是____________，次数是____________。
2、随意掷出一枚均匀的骰子(骰子的六面分别标有1、2、3、4、5、6)，掷出奇数的概率为______________。(填分数)
3、近似数1.96精确到了______位；近似数（保留3个有效数字）为
；水由氢原子和氧原子组成，其中氢原子的直径约为0.米，用科学计数法表示为_____________。
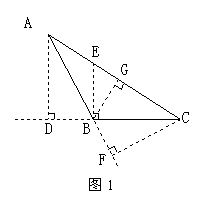
4、如图1，△ABC的边BC上的高是线段___________。
5、当
__________时，单项式
与
是同类项。
6、已知∠1＝
，∠2与∠1互余，则∠2＝_________度。
7、若
，则
＝______________。
8、小王利用计算机设计了一个计算程序，输入和输出的数据如下表：
| 输入 | … | 1 | 2 | 3 | 4 | 5 | 6 | … |
| 输出 | … |
|
|
|
|
|
| … |
那么，当输入的数据是8时，输出的数据是_____________
9、计算：①
＝____________； ②
__;
③
＝__________； ④
＝_______________；
⑤
＝___________；⑥
＝___________________；
⑦
＝__________；⑧
______________.
(
为正整数)
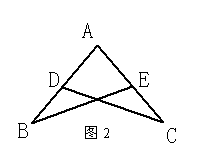10、如图2，已知△ABE≌△ACD，点B和点C是对应顶点，
且∠BEA＝70○，∠A＝80○，则∠C＝__________度。
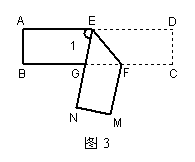11、如图3，一长方形纸条ABCD沿直线EF折叠，
点C、D分别落到点M、N，且∠EFG＝51○，
则∠1＝_____度。
12、当
时，则
____________。
二、选择题（每题2分，共16分）
13、下列计算正确的是（ ）
A.
B.
C.
D.
14、如图4，下列角中与∠B是同位角的有( )
A.∠1 B.∠2 C.∠C D. ∠DAB
15、如图5，方砖除颜色的外完全相同，小老鼠在方砖上自由走
动，最终停留在白色方砖上的概率是（ ）
A.4 B.
C. 
D 
16、
的计算结果是（ ）
A. 
B.
C.
D.
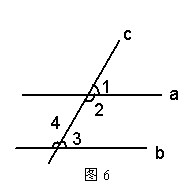
17、如图6，不能推出a∥b的条件是（ ）
A. ∠1＝∠3 B. ∠2＝∠4
C ∠2＝∠3. D. ∠2＋∠3＝180°
18、若
，则
( )
A. 7 B. 12 C. 8 D .9
19、现有两根木棒，它们的长分别是4㎝、6㎝，若要钉成一个三角形的木架，则第三根木棒应从下列四根木棒中选取长为( )的木棒。
A. 10㎝ B. 2㎝ C. 8㎝ D. 12㎝
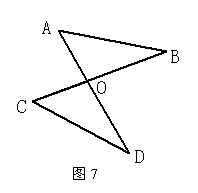
20、如图7，已知直线AD与直线BC相交于点O，
△AOB≌△COD，则下列结论能成立的是（ ）
A..AB∥CD B. ∠B=∠C
C. OB=OC. D. OB = OD
三、设计题：(4分)
21、某公园有一个正方形的花坛(如图所示)，现准备将这个正方形的花坛分成面积相等、形状相同的四块，以便种上不同颜色的花草，应如何设计？请你尽可能精确地画出至少4种设计图。
四、作图题(5分)
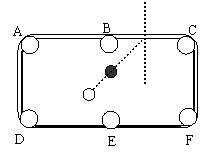22、如图所示：打台球时，用白球沿虚线方向击打黑球，已知入射角等于反射角，请问黑球经过一次反弹后是否会进入F号洞？请你用尺规作图来判断。（请保留作图痕迹，不必写作法、证明）
五、解答题（共53分）
23、计算：(每小题5分，共20分)
①
② 
③ 
④
24、如图，已知直线AB、直线CD被直线EF所截，分别交于G、H，
|
25、解方程：(5分)
|
26、如图，已知点A、B、C与点D、E、F分别在
同一条直线上，直线AF与直线CE、直线BD
分别交于点M、N且 △DNF≌△CMA.
求证：∠3＝∠4.(6分)
证明：∵△DNF≌△CMA（已知）
∴∠1=_______ ， ∠D=∠C
( )
又∵∠1=_______ (已证)
∴_______∥_________( )
∴_______=∠3 ， _______=∠4
( )
又∵∠D =∠C (已证)
∴∠3=∠4 (等量代换)
27、化简求值：(6分)
,其中
.
28、如图①，已知点A、C、D、F在一条直线上，△ABC≌△DEF，
BN平分∠ABC，EM平分∠DEF.
(1) 问：AF与CD相等吗？BN与EM平行吗？请说明你的理由。(6分)
(2)当点C、F在直线AD上移动时(C与点F、点M与点N始终不重合，如
图②、③、④)，其他条件不变，在题(1)中的两个结论还成立吗？若成
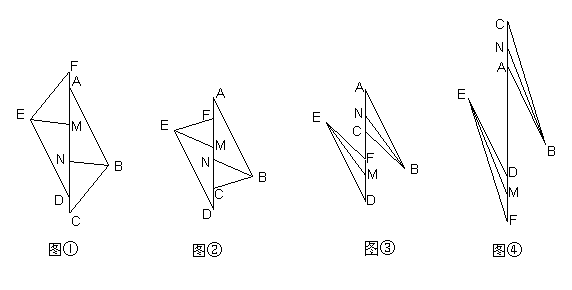立，试选取图②、③、④中的一个图形对其中的一个结论进行说明。(4分)
B卷(满分20分)
一、填空题(每空3分，共15分)
1、如果
，那么
的值是__________________。
2、若
为一个完全平方式，则＝___________。
3、要使
展开后不含
的项，＝_________。
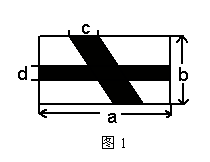
4、如图1，某生活小区有一块长为
米、宽为
米的长
方形绿地，现打算在绿地中建两条小径（阴影部分），
那么建好小径后，绿地的面积为_______________平方米。
5、看图填空
如图2，把一个面积为1的正方形等分成两个面积为 的
矩形，接着把面积为 的矩形等分成两个面积为 的
矩形，再把面积为 的矩形等分成面积为 的矩形，
如此进行下去……
试利用图形揭示的规律计算：
＝____________。
二、解答题
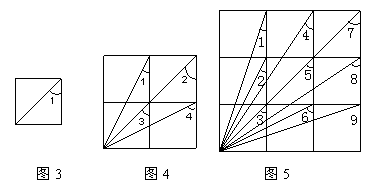6、观察归纳(5分)
(1)如图3，是一个1×1的小正方形，则∠1=______________度；
(2)如图4，是一个2×2的小正方形组成的大正方形，
则∠1+∠2+∠3+∠4=___________度；
(3)如图5，是一个3×3的小正方形组成的大正方形，
则∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8+∠9=________度。
…………………
从上述结论中你发现了什么规律？