第二章 平行线与相交线
【梳理知识】
☆相交线
1、互余与互补(1)概念:①如果两个角的 ,那么这两个角叫做互为余角,简称“ ”;②如果两个角的 ,那么这两个角叫做互为补角,简称“ ”。(2)性质:①余角的性质 ;②补角的性质 .
2、对顶角(1)概念:两条直线相交所成的四个角中,
的两个角叫做对顶角;(2)性质: .
3、“三线八角”
同位角、内错角、同旁内角的概念
☆平行线
1、平行的条件(1) ,两直线平行;(2) ,两直线平行;
(3) ,两直线平行.
2、平行线的特征(1) 两直线平行, ;(2) 两直线平行, ;(3) 两直线平行, ;(4)平行于同一直线的两条直线平行;(5)在同一平面内,垂直于同一直线的两条直线平行.
☆用尺规作一个角等于已知角.
【典例剖析】
例1 (1)一个角的余角比这个角的![]() 还少4°,求这个角的度数.
还少4°,求这个角的度数. 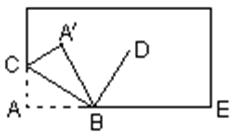
(2)如图,将一张长方形纸的一角斜折过去,使角顶点A落在A'处,BC为折痕,若BD为∠A'BE的平分线,求∠CBD的度数.
例2 (1)如图1,与∠1成同位角的角有 个;与∠1成内错角的角是 ;与∠1成同旁内角的角是 .
(2)如图2,平行线AB、CD与相交线EF、GH相交,图中的同旁内角共有 对.
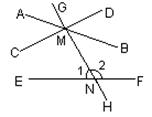
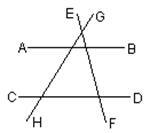
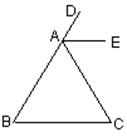
图1 图2 图3
例3 如图3,AE平分∠CAD,AE∥BC,问∠B与∠C有何关系?试说明理由.
例4 已知:如图4,AB∥DE,∠1=∠2,则AE与DC平行吗?完成下列推理,并把每一步的
依据填写在后面的括号内
解:∵AB∥DE (已知)
∴∠1=∠AED ( )
∵∠1=∠2 (已知)
∴∠ =∠ ( )
∴AE∥DC ( )
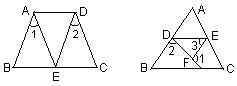
图4 图5
例5 已知:如图5,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的关系,并说明理由.
例6
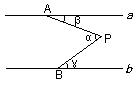
如图,折线APB是夹在两平行线![]() 和
和![]() 之间的一条折线.
之间的一条折线.
(1)试探求∠α与∠β、∠γ之间的关系;
(2)试改变问题中的某些条件时,又有怎样的结论呢?
【同步测试】
1填空题(每小题3分,共24分)
(1)已知∠α=45°,则∠α的余角为 度,补角为 度.
(2)如图,AOE是一条直线,OB⊥AE,OC⊥OD,则图中互余的角有 对,互补的角
有 对.
(3)已知:如图,直线AB和CD相交于O,OE平分∠BOC,且∠AOC=68°,则∠BOE=

(第2题) (第3题) (第4题) (第5题)
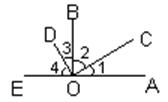
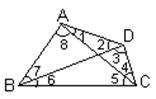
(4)如图,∠1、∠2是两条直线 和 被第三条直线 所截构成的 角.
(5)如图,∠4的内错角是 ,被直线AB所截构成的同旁内角有 对.
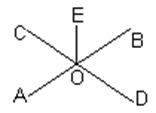
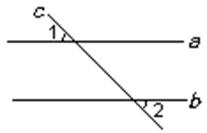
(6)已知:直线c与直线a、b相交,∠1=50°,当∠2= 度时,a∥b.
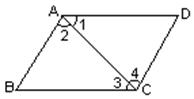
(7)如图所示,要使AB∥CD,只需要添加一个条件,这个条件是 .(填一个你认为正确的条件即可)
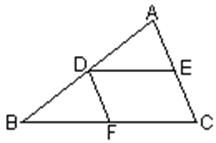
(8)如图所示,DE∥BC,DF∥AC,则图中与∠C相等的角有 个.
(第6题) (第7题) (第8题)
2选择题(每小题4分,共24分)
(9)一个角的补角是它的余角的3倍,则这个角的度数是( )
(A)30° (B)45° (C)60° (D)75°
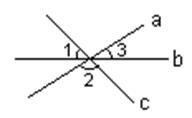
(10)如图,三条直线a、b、c相交于一点,则∠1+∠2+∠3=( )
(A)360° (B)180° (C)120° (D)90°
(第10题) (第11题) (第13题)
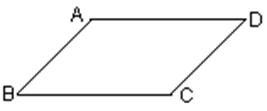
(11)如图,下面推理中,正确的是( )
(A)∵∠A+∠D=180°,∴AD∥BC
(B)∵∠C+∠D=180°,∴AB∥CD
(C)∵∠A+∠D=180°,∴AB∥CD
(D)∵∠A+∠C=180°,∴AB∥CD
(12)如果两个角的一对边在同一直线上,另一对边互相平行,则这两个角( )
(A)相等 (B)互补 (C)相等或互余 (D)相等或互补
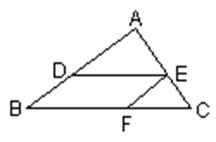
(13)如图,DE∥BC,EF∥AB,则图中与∠BFE互补的角共有( )
(A)2个 (B)3个 (C)4个 (D)5个
(14)下列说法中,错误的是( )
(A)两直线平行,同位角的平分线互相平行
(B)两直线平行,内错角的平分线互相平行
(C)两直线平行,同旁内角的平分线互相平行
(D)两直线平行,同旁内角的平分线互相垂直
3作图题(只保留作图痕迹,每小题5分,共10分)
(15)已知:∠α和∠β(如图),
求作一个角,使它等于∠α+∠β.
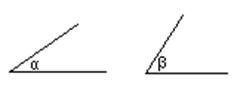
(16)已知:一个三角形的两个角∠A、∠B(如图),
求作第三个角∠C.
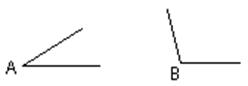
4推理填空(每小题5分,共10分)
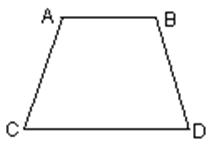
(17)已知:如图,AB∥DC,∠A=∠B,则∠C与∠D相等吗?说明理由.
解:∵AB∥DC (已知)
∴∠A+∠ =180°
∠B+∠ =180° ( )
∵∠A=∠B (已知)
∴∠D=∠C ( )
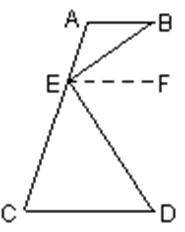
(18)已知:如AB∥CD,∠AEB=∠B,∠CED=∠D,试说明BE⊥DE.
解:作射线EF,使∠AEB=∠BEF(作辅助线)
∵∠AEB=∠B (已知)
∴∠ =∠ ( )
∴ ∥ ( )
∵AB∥CD (已知)
∴ ∥ ( )
∴∠DEF=∠D ( )
∵∠CED=∠D
∴∠ =∠ ( )
∴∠AEB+∠CED=∠BEF+∠DEF
∵∠AEC=180° ( )
∴∠BED=∠BEF+∠DEF=90°
∴BE⊥DE ( )
5解答题(每小题6分,共30分)
(19)如图,AB∥DE,∠A=∠D,AC与DF平行吗?说明理由.
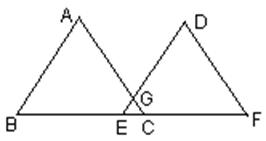
(20)已知:如图,AD⊥BC于D,EG⊥BC于G,交AB于F,交CA延长线于E,且∠AFE=∠E,则AD是∠BAC的平分线吗?

(21)如图,CD⊥AB于D,点F是BC上任意一点,FE⊥AB于E,且∠1=∠2,∠3=80°求∠BCA的度数.
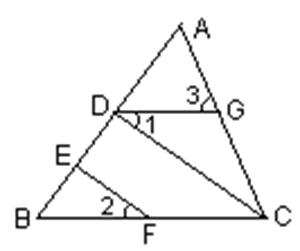
(22)、观察下列图形,寻找对顶角(不含平角)
①两条直线相交(如图1),图中共有 对对顶角;
②三条直线相交于一点(如图2),图中共有 对对顶角;
③四条直线相交于一点(如图3),图中共有 对对顶角;
……
④n条直线相交于一点,则可构成 对对顶角;
⑤2003条直线相交于一点,则可构成 对对顶角;
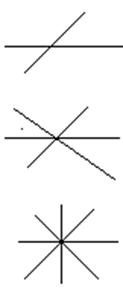
(23)如图,AB∥CD,分别探讨下面四个图形中∠APC与∠PAB,∠PCD的关系,并请你从所得四个关系式中任意选一个说明理由.
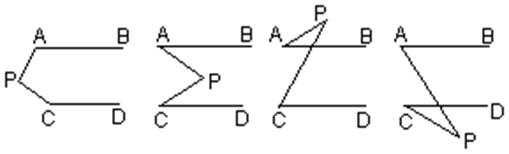
(1) (2) (3) (4)
