七年级数学半期考试试题
班级______ 学号_______ 姓名________
A 卷(100分)
一、 填空题:(每空2分,共18分)
1、写一个一元一次方程________________,使它的解为x=-2
2、已知方程![]() 的解为5,则a的值等于_________.
的解为5,则a的值等于_________.
3、已知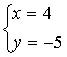 是方程
是方程![]() 的一个解,则k=________
的一个解,则k=________
4、已知二元一次方程![]() ,用含x的代数式表示y,由y=_________.若y的值为2,则x的值为________
,用含x的代数式表示y,由y=_________.若y的值为2,则x的值为________
5、 已知在△ABC中,∠A=∠B+∠C,则此三角形为______三角形.
6、 若等边三角形的两边长分别为3cm和6cm,则它的周长为______
7、 工师傅在做完门框后,为防止变形,通常象右图中所示,
钉上两条斜拉的木板条,(即图中的AB、CD),
![]()
![]()
![]() 这是根据_______数学道理.
这是根据_______数学道理.
8、 个多边形的内角和与外角和为2160•,
则这个多边形的边数为_____
二、 择题:(每题3分,共30分,将正确答案填入下表中)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
1、下列方程中是一元一次方程的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、下列方程变形中,正确的是( )
A、
由![]() ,得
,得![]()
B、
由![]() ,得
,得![]()
C、
由![]() ,得
,得![]()
D、
由![]() ,得
,得![]()
3、在△ABC中,∠A=55,∠B比∠C大25,则∠B=( )
A、50 B、75 C、100 D、125
4、方程组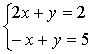 的解是( )
的解是( )
A、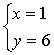 B、
B、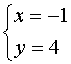 C、
C、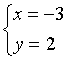 D、
D、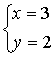
5、下列命题正确的是( )
A、 三角形的角平分线、中线、高线都在三角形的内部。
B、 直角三角形的高线只有一条。
C、 三角形的高线至少有一条在三角形的内部
D、 钝角三角形的三条高都在三角形的外部。
6、以下列各组数据为长度的三条线段能组成三角形的是( )
A、5、8、3 B、5、4、9 C、5、9、5 D、9、4、4
7、已知:如图,三角形ABC的角平分线CD、BE相交于F,
且∠A=60则∠BFC的值为( )
A、80 B、100 C、120 D、140
8、三角形的两边长分别为2和9,第三边长为奇数,则第三边长为:
A、5 B、7 C、9 D、11
9、有一旅客携带了30公斤的行李从南京禄口国际机场乘飞机去天津,按民航的规定,旅客最多可免费携带20公斤的行李,超重部分每公斤按飞机票价格的1.5%购买行李票,现在旅客购买了120元的行李票,则他的飞机票价格应是( )
A、1000元 B、800元 C、600元 D、400元
10、今年春节期间,小明与小红各自得到了一些压岁钱,小明的压岁钱比小红的少836元,小红的压岁钱的6倍比小明的5倍少1284元,设小红的压岁钱为x元,小明的压岁钱为y元,则所列的方程为( )
A、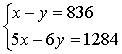 B、
B、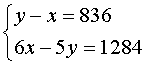
C、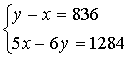 D、
D、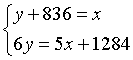
三、 解下列方程(组)
1、![]() 2、
2、
3、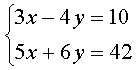 4、
4、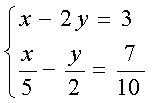
四、 如图,已知△ABC中,AD⊥BC于D,AE为∠BAC的平分线,且∠B=35,∠C=65,求∠DAE的度数(要求能说清楚原因和结论即可)
五、下表是某一周甲、乙两种股票每天的收盘价:(收盘价:股票每天交易结束时的价格)
|
| 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
| 甲 | 12 | 12.5 | 12.9 | 12.45 | 12.75 |
| 乙 | 13.5 | 13.5 | 13.9 | 13.4 | 13.15 |
某人在该周内持有若干甲、乙两种股票,若按照这两种股票每天收盘价计算(不含手续费、税金等),该人帐户上星期二比星期一获利200元,星期三比星期二获利1300元,试问该人持有这两种股票各多少股?
B卷(50分)
一、 填空题:(每题4分,共16分)
1、方程组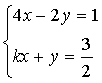 的解中x与y的值相等,则k=________
的解中x与y的值相等,则k=________
2、若一个多边形的内角和与外角和之比是7:2,则这个多边形的对角线有_____条。
|
| x |
|
|
|
| 19 |
| 95 |
|
|
3、如图所示,在![]() 的方格内已填好了两个
的方格内已填好了两个
数19和95,在其余的空格中填入适当的数,
使每一行、每一列以及两条对角线上的三
个数之和都相等,则x=_____-
4、如图,△ABC中,FD⊥BC∠B=∠C,FD⊥BC,
DE⊥AB,∠AFD=158,则∠EDF=_____________
二、
已知方程组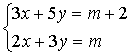 的解也是方程
的解也是方程![]() 的解,求m的值。(10分)
的解,求m的值。(10分)
三、

![]()
![]()
![]() 某纸品厂为了制作两种无盖的长方体小盒(如图(1)(2)所示),利用边角料剪出正方形和长方形两种硬纸片,长方形的宽与正方形的边长相等(如图(3)(4)所示)现将150张正方形硬纸片和300张长方形硬纸片全部用于制作两种小盒,问可以做成甲、乙小盒各多少个?(注:两种小盒是无盖的)(10分)
某纸品厂为了制作两种无盖的长方体小盒(如图(1)(2)所示),利用边角料剪出正方形和长方形两种硬纸片,长方形的宽与正方形的边长相等(如图(3)(4)所示)现将150张正方形硬纸片和300张长方形硬纸片全部用于制作两种小盒,问可以做成甲、乙小盒各多少个?(注:两种小盒是无盖的)(10分)
四、在日常生活中,观察各种建筑物的地板,就能发现地板是由各种正多边形的地砖铺成的,使用给定的某些正多边形,能够拼成一个平面图形,既不留下一丝空隙,又不互相重叠(在几何里叫做平面镶嵌),这显然与正多边形的内角大小有相,当围绕一点拼在一起的几个正多边形的内角和加在一起恰好组成一个周角时,就拼成了一个平面图形
(1)请填写表中的空格:(5分)
| 正多边形的边数 | 3 | 4 | 5 | 6 | …… | n |
| 每个内角的度数 |
|
|
|
| ……. |
|
(2)如果限于一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形?答:____________________________________________(3分)
(3)从正三角形、正方形、正六边形中选一种,再从其他正多边形中任选一种,请画出用两种不同的正多边形镶嵌的平面图形(草图);并探索这两种正多边形共能镶嵌成几种不同的平面图形,说明你的理由。(6分)