第二章 有理数及其运算
2. 1 数怎么不够用了
一、基础训练
1、像5，1.2，
，…这样的数叫做 数；在正数的前面加上“－”号的数叫做 数。
2、0既不是______数，也不是______数。
3、______数和_______数统称有理数。
4、如果上升4m记作+4m，那么下降3m记作__________。
5、如果盈利70元，记作+70元，那么亏损50元记作___________。
6、如果-15人表示缺少劳动力15人，那么+25人表示_____________________。
7、如果零上50C记作+50C，那么零下30C记作________。
8、把下列各数填在相应的大括号：2，－0.3，0，+5，
正数集合
；
负数集合
二、能力训练
1、东、西为两个相反方向，如果－7米表示一个物体向西运动7米，那么+5米表示
_________，物体原地不动记作_______。
2、下列说法错误的是（ ）
A、零不是整数 B、－3是负有理数 C、－0.15是负分数 D、－2.17是负小数。
3、下表记录了某星期内股市的升跌情况，请完成下表：
| 时间 | 升跌情况 | 用正负数表示 |
| 星期一 | 上升100点 | +100 |
| 星期二 | 下跌50点 | |
| 星期三 | 上升60点 | |
| 星期四 | 下跌30点 | |
| 星期五 | 上升2点 |
4、把下列各数分别填入相应集合的大括号里：+5，－7，23，－0.3，0，
－
，8， 17，
整数集合：
分数集合：
正数集合：
负数集合：
2. 2 数 轴
一、基础训练
1、数轴的三要素是______、 _________、 __________。
2、在数轴上原点表示的数是_____，原点右边表示的数是______数，原点左边表示的数
是_________数。
3、－1.3的相反数是_________。
4、
与________互为相反数。 0的相反数是_________。
5、数轴上离开原点5个单位的点表示的数是_____________。
6、指出数轴上A、B、C、D、E各点分别表示的有理数，并用“＜”将它们连接起来。
解：A点表示______；B点表示_____；C点表示______；D点表示____；E点表示________。
用“＜”将它们连接起来是：____________________________________。
7、下列图形中是数轴的是（ ）。
8、比较下列各数的大小。
（1） 0____－２； （2）０．1 ____0．02； （3）－０.1_______ 100；
（4）
_____1； （5）0.01______－99； （6）
______0。
二、能力训练
1、数轴上原点及原点右边的点所表示的数是（ ）
A、负数 B、正数 C、非负数 D、非正数
2、在
，
，
，
，
中最大的数是（ ）
A、
B、
C、 D、
3、大于－３的负整数是______；____________的相反数是它的本身。
4、a，b，c在数轴上的位置如图所示，则a，b，c所表示的数是（ ）
A、a，b，c是正数 B、a，b，c是负数
C、a，b是正数，c是负数 D、a，b是负数，c是正数
5、分别在数轴上画出表示下列各数的点，并用“＜”将它们连接起来。
－３，＋２，０，－４.5 , 
1.3 绝对值
一、基础训练
1、－3的绝对值是______，3的绝对值是_________。
2、绝对值等于5的数是____________。
3、绝对值等于本身的数是________，绝对值最小的数是__________。
4、写出绝对值小于3的所有整数_____________。
5、下面说法正确的是（ ）
A、有理数的相反数一定比0小； B、互为相反数的两个数的绝对值相等；
C、如果两个数的绝对值相等，那么这两个数相等； D、有理数的绝对值一定比0大。
6、下面说法中正确的是（ ）
A、绝对值最小的数是0； B、绝对值相等的两个数相等；
C、－α一定是负数； D、有理数的绝对值一定是正数。
7、计算：（1）
（2）
（3）
（4）
8、比较下列各数的大小，并分别求出它们的绝对值：
7，
，0，－1012，1，－4.1，－０.5，。
二、能力训练
1、写出绝对值大于2 而小于5的所有负整数是_____________。
2、已知
的绝对值是6。
3、正式足球比赛对所用足球的质量有严格的规定。下面是6个足球的质量检测 的结果
（用正数记超过规定质量的克数，用负数记不足规定质量的克数）：
－25， +10， －20，+30，+15，－40。
请指出哪个足球的质量好一些，并用绝对值的知识进行说明。
4、用数轴上的点表示下列各有理数，并求其相反数和绝对值。
－0.5，－３.5, 7, －４.5， －4。
5、 已知有三个数a、b、c在数轴上的位置如下图所示：
则a、b、c三个数从小到大顺序是_______________。
2. 4 有理数的加法（1）
一、基础训练
1、计算：（1）
（2）
（3）
（4）
。
2、如果a与b互为相反数，则a+b=__________。
3、3与－5的和的相反数是_____________。
4、计算：
（1）
（2）
（3）
；
（4）
5、下列计算中，正确的是（ ）
A、
B、
C、
D、
6、下列计算中，错误的是（ ）
A、
B、
C、
D、
7、填空：
（1）
（2）
（3）
（4）
8、A地的海拔高度是21米，B地比A地高68米，则B地海拔高度是_________米。
二、能力训练
1、计算：（1）
（2）
2、判断题：（对的在括号里打上“√”，错的则打上“×”。）
（1）两个负数相加和为负数。（ ）
（2）两个有理数相加和为负数时，这两个有理数一定都是负数。（ ）
（3）两个有理数的和的符号取较大的哪一个加数的符号。（ ）
（4）两个有理数的和为正数，这两个有理数都为正数。 （ ）
（5）两个数相加，和一定大于任何一个加数。 （ ）
3、如果a、b互为相反数，则5×（a+b）=___________。 （ ）
4、计算：
（1）
（2）
5、下列运算中，错误的是（ ）
A、
B、
C、
D、
2. 4 有理数的加法（2）
一、基础训练
1、在有理数加法的运算中，加法的_________律、___________律同样适用。
2、请在括号里填上适当的运算律：
（1）计算：
解：原式=
（
）
=
=
（
）
=
（2）计算：
解：原式=
(
)
=
(
)
=
3、一天早晨的气温为
，中午上升了
，半夜又下降了
，则半夜的气温
是
。
4、用简便方法计算下列各题：
（1）
（2）
（3）
（4）
5、利用有理数的加法解答：
小明存折中有450元，取出80元，又存入150元后，存折中还有多少钱？
二、能力训练
1、计算：
；
2、在横线上填入“＞”、“＜”或“＝”。
（1）
（2）
3、英语竞赛成绩85分以上为优秀。老师将某一组的5名同学成绩简记为： －3，14，
０，＋5，－6，这5名同学的平均成绩是（ ）
A、83 B、87 C、82 D、84
4、仓库内原存粮食4000千克，一周内存入和取出情况如下（存入为正，单位：千克）
2000，―1500，―300，600，500，―1600，―350，问第七天末仓库内还存有粮食
多少千克？
5、黎明电子厂的检修小组乘汽车沿公路检修线路。约定前进为正，后退为负，某天自
A地出发到收工时所走路程（单位：千米）为：
+10，―3，+4，+2，―8，+13，―2，+12，+8，+5。
（1）问收工时距A地有多远？
（2）若每千米耗油0.3升，问从A地出发到收工时共耗油多少升？
2. 5 有理数的减法
一、基础训练：
1、有理数的减法法则是：减去一个数，等于_________这个数的相反数。
2、计算：
（1）
（2）
（3）
（4）
（5）
（6）
3、填空：
（1）
（2）
（3）
（4）
4、下列各式中，运算结果错误的是（ ）
A、
B、
C、
D、
5、下列计算中正确的是（ ）
A、
B、
C、
D、
6、用有理数减法的算式表示：
（1）比20C低80C的温度____________；（2）比-30C低60C的温度________________。
二、能力训练
1、若两数和为14，其中一个加数是－4，则另一个加数是___________。
2、计算：
（1）
（2）
3、选择题：
（1）较小的数减去较大的数，所得的数一定是（ ）
A、0 B、正数 C、负数 D、0或负数
（2）下列说法正确的是（ ）
A、减去一个负数，差一定大于被减数 B、减去一个正数，差不一定小于被减数
C、0减去任何数，差都是负数 D、两个数之差一定小于被减数
（3）下列说法正确的是（ ）
A、减去一个数，等于加上这个数 B、有理数的减法中，被减数不一定比减数大
C、0减去一个数，仍得这个数 D、两个相反数相减得0
（4）差是－5，被减数是－2，则减数是（ ）
A、－７ B、－３ C、３ D、７
４、河里的水位第一天上升８厘米，第二天下降７厘米，第三天又上升了９厘米，第
四天上升了３厘米。问第四天河水水位比刚开始时的水位高多少厘米？
2. 6 有理数的加减混合运算（1）
一、基础训练
1、计算：（1）
（2）
（3）
（4）
2、计算：（1）
（2）
解；原式=
解：原式=
=
=
=________ =________
3、下列交换加数的位置的变形正确的是（ ）
A、1-4+5-4=1-4+4-5 B、
C、
D、
4、计算：（1）
（2）
（3）
（4）
5、某天，广东的温度是180C，而哈尔滨的温度是零下220C，广东比哈尔滨温度高出
（ ）0C。
A、－4 B、4 C、40 D、－40
二、能力训练
1、下列运算的结果错误的是（ ）
A、
B、
C、
D、
2、计算：
的结果是（ ）
A、2002 B、2000 C、－4 D、0
3、计算题：
（1）
（2）
4、开元村有7块土豆实验田，每块实验田今年的产量与去年相比情况如下（增产为正，
减产为负，单位：千克）：67，―35，25，―12，23，―2，7。
今年的土豆总产量与去年相比情况如何？
5、班委会把班费存入银行，使用时再到银行去取。这学期管理的情况如下：存入125元，
取出97元，存入50元，取出38元，取出12.5元，存入100元，取出78元，取出21
元，这时班费还有多少钱？
2. 6 有理数的加减混合运算（2）
一、基础训练
1、请将下列各式中的减法都化为加法：
（1）
（2）
（3）
（4）
2、将下列式子先统一成加法，再写成省略加号与括号的和的形式。
（1）
（2）
3、计算题：
（1）
（2）
（3）
（4）
二、能力训练
1、已知：M=
，N=
，则（ ）
A、M≤N B、M＞N C、M＜N D、M=N
2、计算题：
（1）
（2）
（3）
（4）
3、用不同方法计算：
4、某银行储蓄所办理7件储蓄业务：取出950元，存进500元，取出800元，存进1200元，
存进2500元，取出500元。请你给计算一下，银行现款增加了多少？你能用有理数加减
法表示出来吗？
2. 7 水位的变化
一、基础训练
1、计算题：
（1）
（2）
2、某中学初一（1）班学生的平均身高是160厘米。该班6名学生的身高的情况（单位：
| 姓名 | 小佳 | 小莉 | 小阳 | 小月 | 小华 | 小高 |
| 身高 | 159 | 154 | 165 | |||
| 身高与平均 身高的差 | －１ | +2 | 0 | +3 |
厘米）如下：
分析上述表格显示的情况，回答：
（1）试完成上表；
（2）在小莉、小阳、小月、小高中， 身高最高的是（ ）
A、小莉 B、小阳 C、小月 D、小高
（3）在小佳、小莉、小阳、小月中，身高最矮的是（ ）
A、小月 B、小莉 C、小阳 D、小佳
3、某商店卖水果，苹果进价2元，售出价为2.5，香蕉进价为1.8元，售出价为2.1元,
则卖出一斤苹果和一斤香蕉共赚了________元。
4、小王早晨乘出租车去商店花了10元钱，买了3支铅笔，每支铅笔0.5元，后来他又坐
公交车返回花了2元，他一共花了_________元。
5、李平的存折中有存款3500元，买DVD取出1000元，又存入800元，那么他现在存款
有_________元。
6、某村共有10块香瓜田，今年每块田的收成与去年相比（增为正，减产为负，单位：
千克）的情况如下：55 ，79，－40， ―25，10， ―16， 27，―5， 31， 4。
今年的香瓜总产量与去年相比情况如何？
7、有8头猪要出栏，每头猪的质量如下（单位：千克）：100， 97， 103， 95， 101，
102， 98， 104。你能很快算出它们质量吗？
8、某工厂计划每日生产彩电100台，但实际上一星期的产量如下所示：
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减/辆 | －1 | +3 | －2 | +4 | +7 | －5 | －10 |
比计划的100台多的记为正数，比计划的100台少的记为负数；请你算出本月总产
量是多少台？
二、能力训练
1、计算题：
（1）
（2）
2、下表是小刚记录的五月份20～24日每天最高气温变化情况，且19日的最高气温为260。
| 时间 | 20日 | 21日 | 22日 | 23日 | 24日 |
| 每天最高气温的变化 （与前一天比较） | 升20C | 降30C | 升60C | 降50C | 降40C |
（1）请算出5月22日最高气温是多少度？
（2）这一周哪一天气温最高？
（3）请用折线统计图表示该周5天的气温变化情况。
3、某自行车厂本周计划每天生产100辆自行车。由于工人实行轮休，每天上班人数不
一定相等，实际每日产量与原计划产量对比如下表（超出的辆数为正，不足的辆数为负）
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | －5 | +4 | －3 | +4 | +10 | －2 | －15 |
（1）本周总产量与原计划量相比，增加了（或减少）了多少辆？
（2）日平均产量与计划产量相比，增加了（或减少）了多少辆？
2. 8 有理数的乘法（1）
一、基础训练
1、填空：
（1）
；
（2）
；
（3）
；
（4）
。
2、下列计算正确的是（ ）
A、
B、
C、
D、
3、填空：
（1）
（2）
（3）
（4）
4、
的倒数是______；__________的倒数是5。
5、计算题：
（1）
（2）
（3）
（4）
二、能力训练
1、
的倒数是 ；0.2的倒数是__________。
2、α、b是两个有理数，若αb＞0，则_____________；若αb＜0，则_________________。若αb＝0，则_________________；若αb=1，则___________________。
3、如果5α是负数，则（ ）
A、α＞0 B、α≥0 C、α＜0 D、α≤0
4、若α、b互为倒数，则
。
5、计算：
。
2. 8 有理数的乘法（2）
一、基础训练
1、在下列括号里填上适当的运算律：
（1）
（
）
（2）
（
）
（3）
（
）
2、计算
时，可以使运算简便最出运用（ ）
A、乘法交换律 B、乘法结合律 C、乘法分配律 D、乘法分配律
3、用简便方法运算：
（1）
（2）
（3）
（4）
（5）
二、能力训练
1、计算：
2、计算：
3、计算：
4、用简便方法计算：
。
2. 9 有理数的除法
一、基础训练
| 算式 | 商的符号 | 商的绝对值 | 商 |
| 56÷7 | |||
| （－56）÷7 | |||
| 56÷（－7） | |||
| （－56）÷（－7） |
1、填空：
2、填空：
（1）的倒数是
（2）
的倒数是
（3）
的倒数是
（4）
的倒数是
3、除以一个数，等于乘以这个数的________数。
4、计算：
（1）
（2）
（3）
（4）
5、下列结论中，错误的是（ ）
A、零没有倒数； B、零没有相反数；
C、零不能做除数； D、零除以任何非零的数都得零。
6、两个有理数的商是正数，这两个数一定是（ ）
A、都是正数 B、都是负数 C、至少一个是正数 D、两数同号
二、能力训练
| 数α | α的绝对值 | 的相反数 | α的倒数 |
| －0.75 | |||
| 1.5 | |||
| － | |||
| －0.2 |
1、填空：
2、计算：
3、计算题：
（1）
（2）
4、已知
、
互为相反数，
、
互为倒数，
的绝对值为1。求式子
的值。
2. 10 有理数的乘方（1）
一、基础训练
1、填空：
| 积的形式 | 幂 | 底数 | 指数 |
|
| |||
|
| |||
|
|
|
2、在各题的括号里填上适当的数：
（1）
（2）
（3）
（4）
（5）
。
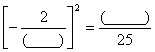3、下列计算对吗？在括号里打上“√”或“×”：
（1）
（ ） （2）
（ ）
（3）
（ ） （4）
（ ）
4、把下列各式写成幂的形式，并计算其值：
（1）
（2）
（3）
（4）
5、+3的平方等于______；－3的平方等于_______；平方等于9的有理数有___个，
是___________。
6、下列说法正确的是（ ）
A、平方得16的数是4 B、一个数的平方不能是负数
C、一个数的平方只能是正数 D、有理数的平方比原数大
二、能力训练
1、平方是25的数有_____个，是______。
2、立方是8的有理数是________，立方是－8的有理数是________。
3、若
4、
（ ）
A、1 B、0 C、2 D、－2
5、计算题：
（1）
（2）
2. 10 有理数的乘方（2）
一、基础训练
1、在
中，它表示的意义是______________，其中底数是______，指数是______，
读作___________,幂是_______。
2、（1）在
中，它表示的意义是________________，其中底数是________，指数是_______，读作_____________，幂是_________。
（2）在
中，它表示的意义是________________，其中底数是______，指数是______，
读作_________________，幂是__________。
3、计算题；
（1）
（2）
（3）
（4）
（5）
（6）
4、的值是（ ）
A、 B、
C、
D、
5、下列运算正确的是（ ）
A、
B、
C、 D、
6、下列各组数中，相等的是（ ）
A、
B、
C、
D、
7、下列各组运算中，其值最小的是（ ）
A、
B、
C、
D、
8、_________平方与它的立方互为相反数。
二、能力训练
1、下列各式中，计算结果得0的是（ ）
A、
B、
C、
D、
2、下列计算正确的是（ ）
A、
B、
C、
D、
3、若
，
，
，则下列大小关系中，正确的是（ ）
A、
B、
C、
D、
4、
的计算结果是（ ）
A、－4 B、－8 C、0 D、4
5、下面一组按规律排列的数；1，2，4，8，16，…，第2004个数应是（ ）
A、
B、
C、
D、以上答案均不对
2. 11 有理数的混合运算
一、基础训练
1、请在括号里填上适当的运算顺序：
（1）计算：
（2）
解：原式=
（
） 解：原式=
（ ）
=
（
） =
（ ）
=
（
）
=
（
）
2、计算
第一步最好运用（ ）
A、加法交换律 B、按顺序计算 C、加法结合律 D、乘法分配律
3、计算
能使运算简便的是（ ）
A、加法交换律 B、按顺序计算 C、加法结合律； D、乘法分配律
4、计算题：
（1） ；
（2）
；
（3）
；
（4）
。
5、下列各数
，
，
，
，
中，负数的个数是（ ）
A、1个 B、2个 C、3个 D、4个
二、能力训练
1、计算：
；
2、
的值为 （ ）
A、
B、
C、1 D、
3、计算题：
（1）
； （2）
4、通过观察下列各式：
，
，
，…，可猜想到有如
下规律（用自然数n表示）：_______________________________________________。
2. 12 计算器的使用
一、基础训练
1、用计算器求3.12÷(-0.4)的按健顺序正确的是（ ）
A、3 1 · 2 ÷ （+） 0 · 4 =
B、3 1 · 2 ÷ （-） 0 · 4 =
C、3 · 1 2 ÷ （-） 0 · 4 =
D、3 1 · 2 ÷ （+） 0 · 4 =
2、用计算器求62.2+4×7.8的按键顺序正确的是（ ）
A、6 2 · 2 + 4 7 · 8 × =
B、· 6 2 2 + 4 × 7 · 8 =
C、6 2 · 2 + 4 × 7 · 8 =
D、以上都不正确。
3、用计算器计算124×
，按键的顺序为 ( )
4、用计算器求
，按键顺序应为__________________。
5、用计算器求
，按键顺序应为_________________。
6、用计算器计算
，具体按键顺序应为_______________。
二、能力训练
1、用计算器计算，并写出按键顺序：
（1）
（2）
（3）
2、用计算器求值：
（1）0.32+8.68 （2）80÷8-30×3
（3）6.322-4.162 （4）1.352+0.862
3、用计算器计算并观察：
1.22=? 0.122=? 0.0122=? 122=? 1202=?,你发现了什么规律?
4、用计算器计算下列各式,将结果填写在横线上
999 ×21=___________ 999 ×22=____________
999 ×23=___________ 999× 24=_____________
(1)你发现了什么?
(2)不用计算器,你能直接写出999× 29的结果吗?
单 元 复 习
一、本章重要知识点
1、有理数包括_____数和____数。其中___数、____数和0统称为整数；____数和____数
统称为分数。
2、数轴：（1）数轴的三要素是______ 、 ________和_______。
（2）有理数的大小比较：数轴上表示的两个数，右边的数总比_____边的数大。
正数大于0，负数小于0，正数大于负数。两个负数，绝对值大的反而_____。
3、相反数：如果两个数只有符号不同，那么我们称其中一个数为另一个数的_________数。
4、绝对值：正数的绝对值是它本身，负数的绝对值是它的______数，零的相反数是____。
5、有理数的加法法则：
（1）同号两数相加，取_______的符号，并把绝对值_______。
（2）异号两数相加，绝对值相等时和为_____；绝对值不等时，取绝对值较大的____的符
号并用较大的绝对值__________较小的绝对值。
（3）一个数同0相加，仍得________。
6、有理数的减法法则：减去一个数等于加上这个数的_________数。
7、有理数的乘法法则：
两数相乘，同号得______，异号得_______，并把绝对值_________。
8、有理数的除法法则：
（1）两数相除，同号得______，异号得_______，并把绝对值_________。
（2）除以一个数等于乘以这个数的__________数。
9、有理数的混合运算法则：
先算______，再算_____，最后算加减；如果有括号，先算括号里面的。
二、基础训练
1、如果把长江的水位比警戒水位高0.2米，记作＋0.2米，那么比警戒水位低0.15米，
记作_________米。
2、
的相反数是 ，倒数是 ，绝对值是 。
3、在数轴上，距原点2个单位长度的点表示的数是 。
4、在
，0，－(－1.5)，－│－5│，2，
，－24中，负数有 个，整数有 个。
5、用“＜ ”、“＞”或“＝”连接：
（1）－2 ＋6 ； （2） 0 －1.8 ； （3）
_____ 
.
6、A地海拔高度是－30米，B地海拔高度是10米，C地海拔高度是－10米，则 地势最高，_____地势最低，地势最高的与地势最低的相差______米。
7、七年级（6）班有x名学生，其中女生人数占45％，则男生人数是 人；若本班有60人，则男生人数有 人。
8、平方是25的有理数是 ，绝对值等于3的数是 。
9、在数轴上，与点的距离为5个单位的点有 个，它们是
10、小明乘电梯从地下2层升至地上8层，电梯一共升了 层。
11、若、互为相反数，
、互为倒数，则
。
12、立方得
的数是
。
13、在(－1)2003，(－1)2004，－22，(－3)2这四个数中，最大的数与
最小的数的和等于 （ ）
A.、6 B、8 C、－5 D、 5
14、 下列说法中正确的是 （ ）
A、最小的整数是0 B、有理数分为正数和负数
C、如果两个数的绝对值相等，那么这两个数相等 D、互为相反数的两个数的绝对值相等
15、学校、家、书店依次座落在一条南北走向的大街上，学校在家的南边20，书店在家北边100，张明同学从家里出发，向北走了50，接着又向北走了-70，此时张明的位置在（ ）
A、在家 B、 学校 C、 书店 D、 不在上述地方
三、能力训练
16、计算下列各题：
（1）
（2）
（3）
（4）
（5） －17＋23＋(－16)－(－7)
（6） 1
（7）（－12）÷（－3）+4÷(-2²)
（8） 
17、化简下列各数，并在数轴上把它们表示出来。
，
，
，
18、某商场老板对今年上半年每月的利润作了如下记录：1、2、5、6月盈利分别是13万元、12万元、12.5万元、10万元，3、4月亏损分别是0.7万元和0.8万元。试用正、负数表示各月的利润，并算出该商场上半年的总利润额。
19、流花河的警戒水位是
米，下表记录的是今年某一周内的水位变化情况，取河流的警戒水位作为
点，并且上周末（星期六）的水位达到警戒水位，正号表示水位比前一天上升，负号表示水位比前一天下降。
| 星期 | 日 | 一 | 二 | 三 | 四 | 五 | 六 |
|
|
|
|
|
|
|
| |
| 水位变化（米） |
|
|
|
|
|
|
|
⑴本周哪一天河流的水位最高？哪一天河流的水位最低？它们位于警戒水位之上还是之下？
⑵与上周末相比,本周末河流的水位是上升了还是下降了？
⑶以警戒水位作为零点，用折线统计图表示本周的水位情况。
水位变化（米）
日 一 二 三 四 五 六 星期
单元测验试题
（时间为45分钟，满分为100分）
一、选择题（每小题3分，共30分）
1、在
，
，
， ，
中，负数的个数有（ ）
A、
个 B、个
C、
个
D、
个
2、一个数加上
等于
，则这个数是（ ）
A、
B、
C、
D、-7
3、
的相反数是（ ）
A、
B、 C、-
D、
4、比较
, 
, ，的大小，下列正确的（ ）
A、 > > > B、 > >>
C、 > > > D、
> >>
5、乘积为的两个数叫做互为负倒数，则的负倒数是（ ）
A、 B、
C、 D、
6、若两数的绝对值相等，则这两数（ ）
A、相等 B、互为相反数 C、一定是0 D、相等或互为相反数
7、0是（ ）。
A、正数 B、负数 C、整数 D、无意义的数
8、若a是一个有理数，则（ ）
A、（－a）一定是负数 B、a一定是正数 C、a一定不是负数 D、a2必是正数
9、在数轴上可以找到（ ）
A、最大的数 B、最小的数 C、最小的负数 D、最小的正整数
10、在数轴上表示－10和3的两点的距离是（ ）
A、10 B、－10 C、3 D、13
二、填空题（每小题3分，共15分）
11、把下列各数填在相应的大括号中
8，，0.275，0，
，，，
整数集合
分数集合
12、如果向南走
米记为是
米，那么向北走
米记为是 , 0米的
意义是
13、最大的负整数是 ，最小的正整数是 。
14、在-
中的底数是
，指数是
。
15、
＋
=
。
三、解答题（每小题6分，共30分）
16、观察下列算式：
，
，
，
，
请你在观察规律之后并用你得到的规律填空：
17、计算：
+
+
+
18、计算： 
19、计算：
20、计算：100
四、解答题（21、22题每题8分，23题9分，共25分）
21、下图是一个数值转换机示意图，请按要求在括号内填写转换步骤，在表格中填写数值。
输入a
（ ）
输入 －1
输出
0
（ ）
（ ）
 | |  | |||
输出
22、某地探空气球的气象观测资料表明，高度每增加1千米，气温大约降低6℃。若该地
地面温度为21℃，高空某处温度为－39℃，求此处的高度是多少千米？
23、“十一”黄金周期间，我区九峰公园在7天假期中每天的人数变化如下表，（正数表示比前一天多的人数，负数表示比前一天少的人数）
| 日 期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
| 人数变化 单位:万人 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(1)设10月3日的游客人数为a万人,请用含a的代数式表示10月4日的游客人数.
(2) 若以9月30日的游客人数为0点,用折线统计图表示这7天游客人数情况
第二章 有理数及其运算
2.1数怎么不够用了
一、1、正、负； 2、正、负； 3、整、分； 4、-3m； 5、-50元； 6、增加劳动力25人；
7、-30C； 8、
二、1、向东运动5米、0； 2、A； 3、-50、+60、-30、+2； 4、整数集合：+5、-7、23、0、8、17；分数集合：
、、
；正数集合：+5、23、8、17、；负数集合：-7、
、；5、略。
2.2数轴
一、1、正方向、原点、单位长度； 2、0，正，负； 3、1.3； 4、
，0； 5、
；
6、-1.5，0.5,1,-0.5,2，-1.5<-0.5<0.5<1<2； 7、A 8、（1）＞，（2）＞，（3）＜
（4）＜，（5）＞，（6）＞；
二、1、C ； 2、D； 3、-2，-1，0；4、D、 5、略。
2.3绝对值
一、1、3，3； 2、±5； 3、正数和0，0； 4、±2，±1，0； 5、B； 6、A； 7、（1）8.5,
(2)2.4,(3)
,(4)3； 8、略。
二、1、-4，-3； 2、±2.5，±6； 3、略 4、略 5、
＞ ＞。
2.4有理数的加法（1）
一、1、（1）-30，（2）-6，（3）-18，（4）0； 2、0； 3、2； 4、（1）
，（2）1，
（3）0.7，（4）7； 5、B； 6、C； 7、（1）-13，（2）+17，（3）94，（4）0； 8、89。
二、1、（1）9，（2）-60； 2、（1）√（2）×（3）×（4）×（5）×； 3、0； 4、（1）
，（2）
； 5、D。
2.4有理数的加法（2）
一、1、交换、结合； 2、（1）结合律、结合律；（2）交换律、结合律； 3、-3； 4、（1）-15、
（2）-90、（3）-30、（4）-16； 5、520元。
二、1、-5； 2、（1）=、（2）＜；3、B； 4、3350； 5、（1）41千米、（2）20.1升。
2.5有理数减法
一、1、加上； 2、（1）+4，19 （2）-4，11 （3）4，-11 （4）-4，-19 （5）-10.24,-10.24
（6）
，； 3、（1）29 （2）-115 （3）17 （4）12； 4、D； 5、B； 6、（1）
-60C， （2）-90C；
二、1、18； 2、（1）40，（2）-5， 3、（1）C （2）A （3）B （4）C； 4、13厘米。
2.6有理数加减混合运算（1）
一、1、（1）3 （2）-5 （3）-3 （4）-7； 2、（1）14.5,(2)+9.8； 3、C； 4、
（1）-30 （2）
（3）-6，（4）1； 5、C。
二、1、D； 2、C； 3、（1） （2）4； 4、增产73千克； 5、28.5元。
2.6有理数加减混合运算（2）
一、1、略 2、（1）-40-27+19-24+32， （2）-9+2-3-4； 3、（1）
，（2）-2
（3）-73 （4）
。
二、1、B； 2、（1），（2）1 （3）
（4）9； 3、略； 4、1950。
2.7水位的变化
一、1、（1）30 （2）9；2、（1）略 （2）D （3）A ；3、0.8； 4、13.5； 5、3300；
6、增产120千克； 7、800； 8、699。
二、1、（1）68.9 （2）-6 ；2、（1）31 （2）22日 （3）略；3、略。
2.8有理数的乘法（1）
一、1、（1）-48，（2）6.3 （3）0 （4）1； 2、C； 3、（1）
，（2）
，（3）1
（4）0； 4、，
； 5、（1）0，（2） （3）
，（4）1。
二、1、
，5；2、
同号，异号，
，互为倒数；
3、C； 4、0；5、-2。
2.8有理数的乘法（2）
一、1、（1）乘法结合律 （2）乘法结合律和交换律（3）乘法分配律；2、C；
3、（1）5，（2）
（3）15 （4）100（5）
二、1、2； 2、7； 3、1； 4、
。
2.9有理数的除法
一、1、略； 2、（1）
，（2）
，（3）-4 （4）
； 3、倒；4、（1）-2 （2）
3 （3）0 （4）
； 5、B； 6、D。
二、1、略； 2、-1； 3、（1）
（2）； 4、1或-1。
2.10有理数的乘方（1）
一、1、略； 2、（1）4，（2）81，（3）-3，（4）3，49，（5）5，4； 3、（1）√（2）×
（3）√（4）√
； 4、（1）
（2）
（3）
（4）
；
5、9，9，2，±3； 6、B；
二、1、2，±5； 2、-2； 3、2； 4、B； 5、（1）-8， （2）
。
2.10有理数的乘方（2）
一、1、
，3，2，3的平方的相反数，-9； 2、（1）
，-2，4，-2的四次方，16；（2）
，2，4，2的四次方的相反数，-16；
3、（1）
（2）-25（3）-4（4）
（5）（6）-1；4、A； 5、B； 6、C；
7、A 8、-1。
二、1、A； 2、A； 3、C； 4、B； 5、C。
2.11有理数的混合运算
一、1、（1）先算乘方，再算乘法，最后算加法（2）先算乘方，再算除法，最后算减法。
2、A； 3、D； 4、（1），（2）22，（3）42，（4）
； 5、C。
二、1、
； 2、A； 3、（1）0，（2）3； 4、
2.12计算器的使用
（略）
有理数及其运算单元总复习
一、1、整，分，正整，负整，正分，负分； 2、（1）正方向，原点，单位长度；（2）左；
3、相反， 4、相反，0； 5、（1）相同，相加（2）0，加数，减去（3）这个数； 6、相反； 7、正，负，相乘； 8、（1）正，负，相除（2）倒；9、乘方，乘除 。
二、1、-0.15； 2、
，
，； 3、±2； 4、3，4； 5、＜，＞，＜；6、B，A，40；
7、55%x， 33； 8、±5，±3； 9、2，-8或2；10、10； 11、2； 12、-3； 13、D；
14、D； 15、B。
三、16、（1）-3，（2），（3）-3，（4）-26，（5）-3，（6）
，（7）3，（8）22；17、略；
18、46万元；19、略。
有理数及其运算单元测验试题
一、1、A； 2、B； 3、A； 4、C； 5、C； 6、D； 7、C； 8、C； 9、D； 10、D。
二、11、整数集合：8，0，-6，┃-2│，分数集合：，0.275,,-0.25；12、-700米，
表示原地不动； 13、-1，1； 14、
，2；15、0。
三、16、48，52，4； 17、4； 18、-4； 19、-7； 20、22。
四、21、 （略） 22、10千米； 23、（1）(a-0.4)万人，（2）略。