七年级数学期末考试模拟测试　 2004-05-13

班级_________ 姓名___________成绩___________

一.选择题（每小题3分，计30分）

1、若代数式7—2x和5—x的值互为相反数，则x的值为（　　　）

　　A　4　　 B　2　　 C　　　　D　

2、如图，AB∥ED，则∠A＋∠C＋∠D＝（　　）

A．180°　 B．270°　　　 C．360° 　　　 D．540°

3、下列条件中，不能判定三角形全等的是　　　　（　　  ）

A、三条边对应相等　 B、两边和一角对应相等　C、两角的其中一角的对边对应相等

D、两角和它们的夹边对应相等

4、小明用一枚均匀的硬币试验，前7次掷得的结果都是下面向上，如果将第8次掷得下面向上的概率记为P，则　　 （　　 ）

A、P=1/2　　B、P＜1/2　　C、P＞1/2　 D、无法确定

5、某班在组织学生议一议：测量1张纸大约有多厚。

出现了以下四种观点，你认为较合理且可行的观点是（　　）

A、 直接用三角尺测量1张纸的厚度　

B、 先用三角尺测量同类型的2张纸的厚度

C、 先用三角尺测量同类型的100张纸的厚度

D、 先用三角尺测量同类型的1000张纸的厚度

6、下列说法中错误的是（　 ）

A、三角形的中线、角平分线、高线都是线段；

B、任意三角形的内角和都是180°；

C、三角形按边分可分为不等边三角形和等腰三角形；

D、三角形的一个外角大于任何一个内角。

7、已知三角形的三边分别为2，，4那么的取值范围是（　　 ）

 A、　　 B、　　 C、　　　 D、

8、在一个三角形，若，则是（　　　）

 A、直角三角形　　B、锐角三角形　 C、钝角三角形　 D、以上都不对

9、一辆汽车以平均速度60千米/时的速度在公路上行驶，则它所走的路程s（千米）与所用的时间t（时）的关系表达式为（　　 ）

A、　B、　C、　D、

10、正五边形的对称轴共有（　　　）

A、2条　　 B. 4条　　 C. 5条　　 D.无数条

11、等腰三角形的一边等于3，一边等于6，则它的周长等于（　　）

A、12　 B、12或15　 C、15或18　 D、15

 

12、下列图形中，不是轴对称图形的是　　 （　 ）

 

A　　　　　　　  B　　　　　　　　 C　　　　　　　　　　　  D

一、　　　　 填空题（每小题3分，计30分）

1、多项式3a² b + 2b –1第三项的系数是____________，次数是____________.

2、等腰三角形一个底角为36°，则此等腰三角形顶角为___________。

3、以下四个事件，它们的概率分别为多少，填在后面的横线上。　

事件A：在一小时内，你步行可以走80千米，则P（A）=＿＿＿；

事件B：一个普通的骰子，你掷出2次，其点数之和大于10，则P（B）=＿＿＿；

事件C：两数之和是负数，则其中必有一数是负数，则P（C）=＿＿＿。

4、在“变量之间的关系”一章中，我们学习的“变量”是指自变量和因变量，而表达它们之间关系的通常有三种方法，这三种方法是指＿＿＿＿＿＿＿、＿＿＿＿＿＿＿和＿＿＿＿＿＿＿。

5、如图，有一块三角形的土地，现在要求过三

角形的某个顶点画一条线段，将它的面积平均分

成两份，你认为这条线段应该如何画＿＿＿＿＿＿＿

＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿；为什么？＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。

6、把一张写有“A、B、C、D、E、1、2、3、4、5”字母和数字字样的长方形纸条，平放在一张平面镜前的桌子上，则镜子里纸条上的字母和数字不改变的是＿＿＿＿＿＿＿＿＿＿。

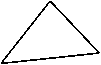
7、如图，已知DE是AC的垂直平分线，AB=10cm，BC=11cm，则ΔABD的周长为＿＿＿＿cm。

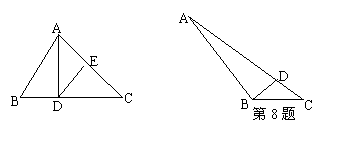
8、如图，∠A=20，∠C=40，∠ADB=80，则∠ABD=＿＿＿，∠DBC=＿＿＿，图中共有等腰三角形＿＿＿个。

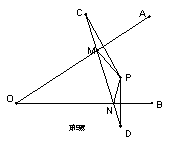
9、如图，点P关于OA、OB的对称点分别为C、D，连结CD，交OA于M，交OB于N，若PMN的周长=8厘米，则CD为 ＿＿＿厘米。

10、将一个30厘米5厘米的长方形纸片折成3厘米5厘米的手风琴状，这样此纸片共有＿＿＿条折痕，再将手风琴中挖去一个任意的三角形，则这个长方形的纸片最多可数出＿＿＿个轴对称图形。

8一根竹竿长3.649米。精确到十分位是　　米；银原子的直径为0 .0003微米，相当于　 米

9今天数学课上，老师讲了多项式的加减，放学后，小明回到家拿出课堂笔记，认真的复习老师课上讲的内容，他突然发现一道题：（-x²+3xy-y²）-（-x²+4xy-y²）=-x²_____+y²空格的地方被钢笔水弄污了，请你帮他补上！

三、作图题（本题5分）

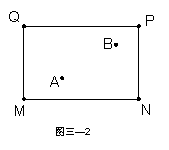如图（三—2），台球桌上有一球A，怎样去

击打球A依次撞击边框MN、NP反射后，撞击

到B球。（画出示意图，不写画法，保留画图

痕迹）（本题A班做）

1、　

四、解答题（1）、（2）各4分、2题5分，计13分

1、（1）2（m＋1）²－(2m＋1)(2m－1)　　　　　　　  （2）

（3），其中

2、　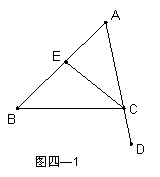如图（四—1）在△ABC中，∠B=40，∠BCD=100，EC平分∠ACB，求∠A与∠ACE的度数。

五、证明题（每小题6分，计12分）

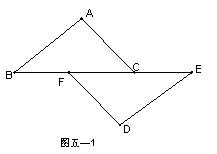1、如图（五—1），点B、F、C、E在同一条直线上，FB=CE，AB∥ED ，AC∥FD ，

求证：AB=DE、AC=DF

2、如图，已知，均为等边三角形，BD、CE交于点F。　　

（1）求证：BD=CE

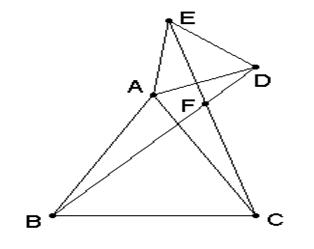（2）求锐角的度数。

六、探究题（本题10分）

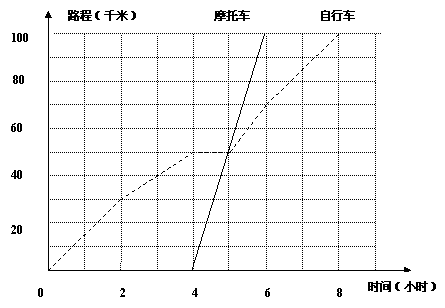　　 甲、乙两人（甲骑摩托车，乙骑自行车）从A城出发到100千米处的B城旅游，如右图表示甲、乙两人离开A城路程与时间之间的关系图象。

1、　分别求出甲、乙两人这次旅程的平均速度是多少？

2、　根据图象，你能得出关于甲、乙两人旅行的那些信息？

注：回答2时注意以下要求：

（1）请至少提供三条相关信息，如由图象可知，乙比甲早出发4小时（或甲比乙晚出发4小时）等；（2）不要再提供（1）列举的信息。

28、（本题11分）乘法公式的探究及应用.

（1）如左图，可以求出阴影部分的面积是　　　　　　 （写成两数平方差的形式）；　

（2）如右图，若将阴影部分裁剪下来，重新拼成一个矩形，它的宽是　　　　　　  ，长是　　　　　　 ，面积是　　　　　　　 （写成多项式乘法的形式）

（3）比较左、右两图的阴影部分面积，可以得到乘法公式　　　　 （用式子表达）

（4）运用你所得到的公式，计算下列各题：

　　　　 ①　　　　　　　　　　 ②