第六、七章测试卷(七年级下)
班级___________姓名____________
一、填空能手 看谁既快又准确(每格3分,第4、8题每格1分,共30分).
1、 我国从1949年到1999年的人均寿命统计中,人均寿命统计随时间的变化而发生变化。在这个变化过程中,自变量是____________,因变量是_________________。
2、 角是轴对称图形,它的对称轴是______________________________,等边三角形有
__________条对称轴
3、
如图:在![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,
,![]() ,垂足为
,垂足为![]() ,如果
,如果![]() ,那么
,那么![]() __________
__________![]()
4、 根据关系式y =2x -6,填写下表:
| x | 5 | 6 | 7 | 8 | 9 |
| y | 4 | 8 |
5、
设地面气温是![]() ,如果每升高1km,气温下降
,如果每升高1km,气温下降![]() ,求气温t(
,求气温t(![]() )与高度h(
)与高度h(![]() )的关系式是__________
)的关系式是__________
6、 找出规律,在横线上填上适当的图形,
7、 等腰三角形的一角为50度,则另外两个角是_________________。
8、假定甲、乙两人在一次赛跑中,路程![]() 与时间
与时间![]() 的关系如图,我们可以知道:
的关系如图,我们可以知道:
1、这是一次__________米赛跑
2、甲、乙两人中__________先到终点
3、乙在这次赛跑中速度为__________米/秒
二、看谁的命中率高(每题小题3分,共24分).
1、 下列图案是我国几家银行的标志,其中轴对称图形有( )
(A)1个 (B)2个 (C)3个 (D)4个
2、
在三角形的面积计算公式S =![]() ah中,当底边a一定时,变量是( )
ah中,当底边a一定时,变量是( )
(A)S和a (B)S和h (C)a和h (D)S,a和h
3、 等腰三角形一边是3,另一边是6,那么它的周长等于( )
(A)12 (B)12或15 (C)15 (D)15或18
4、 黑板上写着 在正对着黑板的镜子里的像是( )
(A) (B) (C) (D)
5、 一蓄水池里有水40m3,每分钟放出2 m3的水,水池中的水量与放水时间有如下关系:
| 放水时间/分 | 1 | 2 | 3 | 4 | … |
| 水池中水量/ m3 | 38 | 36 | 34 | 32 | … |
下列数据中满足此表格的是( )
(A)放水时间8分,水池中水量25 m3 (B)放水时间20分,水池中水量4 m3
(C)放水时间26分,水池中水量14 m3 (D)放水时间18分,水池中水量4 m3
6、
如图所示,在![]() 中,
中,![]() ,
,![]() 是
是![]() 上的点,则以下判断正确的是:( )
上的点,则以下判断正确的是:( )
①若![]() ,则
,则![]() ; ②若
; ②若![]() ,则
,则![]() ;
;
③若![]() ,则
,则![]() ; ④若
; ④若![]() ,则
,则![]()
(A) ①④ (B) ②④ (C)①②③ (D)①②③④
7、开始行驶时,油箱内有油50升,如果汽车行驶每时耗油5升,则油箱内余油量Q(升)与行驶时间t(时)的关系的图象是( )

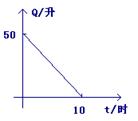
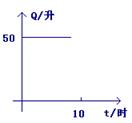
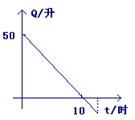
(A) (B) (C) (D)
8、根据如图所示的程序,当输入的![]() 时,输出的
时,输出的![]() 的值是(
)
的值是(
)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
三 想一想,做一做:(第1题6分,其它每题10分,共46分)
1、作图:
下图是在方格纸上画出的一个风筝的一半,以![]() 为对称轴画出风筝的另一半。(6分)
为对称轴画出风筝的另一半。(6分)
2、如图:已知![]() 中,
中,![]() ,
,![]() 的中垂线交
的中垂线交![]() 于
于![]() ,垂足为
,垂足为![]() ,
,
![]() 的周长为
的周长为![]() ,求
,求![]() 的长。(10分)
的长。(10分)
3、如图表示的是某港口某日从0时到15时的水深变化情况
①大约什么时候港口的水最深?深度约是多少?(2分)
②大约什么时候港口的水最浅?深度约是多少?(2分)
③在什么时间范围内,港口水深在增加?(1分)
④在什么时间范围内,港口水深在减少?(1分)
⑤A、B两点分别表示什么?(2分)
⑥说说这个港口从0时到15时的水深是怎样变化的?(2分)
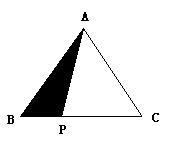
4、 已知![]() 中,
中,![]() ,
,![]() 的面积是18。在
的面积是18。在![]() 上有一点
上有一点![]() ,
,![]() x,设阴影部分的面积为y。
x,设阴影部分的面积为y。
(1) 试写出图中阴影部分的面积y与x之间存在确定的关系式?(3分)
(2) 当![]() 时,求阴影部分的面积?(3分)
时,求阴影部分的面积?(3分)
(3) 点P在什么位置时,△ABC的面积是阴影部分的面积的3倍?(4分)
5、 分析下面反映变量之间关系的图,想像一个适合它的实际情境。
横轴表示__________,纵轴表示__________(4分)
设计一个情景:(6分)

附加题:(每题5分,共20分)
1. 已知![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,
,
则![]() __________
__________
2.已知关系式![]() ,若
,若![]() 随着
随着![]() 的增大而减小,则
的增大而减小,则![]() 是( )
是( )
(A)![]() >
>![]() (B)
(B)![]() <
< ![]() (C)
(C)![]() (D)
(D)![]()
3.某气象研究中心观测一场沙尘暴从发生到结束的全过程。开始时风速平均每时增加
2千米/小时;4时后,沙尘暴经过开阔荒漠地,风速变为平均每时增加4千米/小时;
有一段时间,风速保持不变;当沙尘暴遇到绿色植被区时,其风速平均每时减少
1千米/小时,最终停止。结合风速与时间的图象,回答下列问题:
(1)在纵轴( )内填入相应的数值;
(2)沙尘暴从发生到结束,共经过多少时间?