第五章考試卷
班級_________ 學號________ 得分_______
一、填空題：（50分）
1、 （1）三角形任意两边之和_________第三边。
（2）三角形任意两边之差_________第三边。
（3）三角形三内角的和等于_________。
（4）直角三角形的两个锐角_________。
（5）全等图形的_________和_________都相等。
（6）全等三角形的_________相等，对应角________。
（7）三角形全等的四种判定方法是_________，_________，_________，_________，
另外直角三角形还有一种是__________。
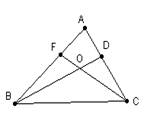
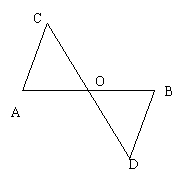
2、如右图，在⊿ABC中∠ABC 和∠ACB的角平分线相交于O，∠BOC=116度，
求∠A的度数_________。
6*、AD是⊿ABC的中线。⊿ABD的周长比⊿ADC的周长大4，则AB与AC的差为_________。
4、如图，a，b，c分别表示⊿ABC的三边，
那么a，b的夹角是 ，b，c的夹角是 ，
∠B是 和 的夹角，a是 和 的夹边。
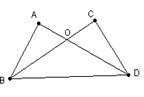5、如图，已知∠A =∠C，
要证明⊿AOB≌⊿COD,
根据“ASA”还要一个条件__________。
_
2、如图2，沿AM折叠，使D点落在BC上的N点处，如果AD=7cm，DM=5cm，∠DAM=300，则AN= cm，NM= cm，
∠NAM= ；
3、如图，∠D=∠B， ∠DAC =∠BAC
解：∵在⊿ABC和⊿ADC中
∠D=∠B
∠DAC =∠BAC
AC=AC
∴⊿DAC≌⊿BAC（ ）
∴BC = DC （ ）
二、選擇題：(20分)
1、下列4组线段能组成三角形的是（ ）
A、3， 3， 6 B、3.1， 3， 6 C、1， 2， 1 D、3， 2，1
2、三角形的高（ ）
A、在边上 B、在三角形内
C、在三角形外 D、以上均可
3、 如果一个三角形的三条高的交点恰是三角形的一个顶点，那么这个三角形是（ ）
A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角三角形
4、若⊿ABC≌⊿DEF那AC的对应边是（ ）
A、DE B、DF C、EF D、BC
5、如图加条件能满足AAS来判断⊿ACD≌⊿ABE的条件是（ ）
A、∠AEB =∠ADC ∠C=∠D
B、∠AEB=∠ADC CD=BE
C、 AC = AB AD = AE
D、 AC = AB ∠C =∠B
6、下列由几根木条用钉子钉成如下的模型，其中在同一平面内不具有稳定性的是（ ）
 |
A B C D
7、两个直角三角形全等的条件是（ ）
A、一个锐角对应相等 B、两个锐角对应相等
C、一条边对应相等 D、两条边对应相等
8、如图，某人不小心把一块三角形的玻璃打碎成三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的方法是
（ ）
|
A 带①去
B 带②去
|
|
 |
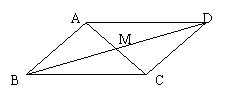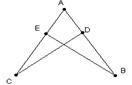
9、如图，AB=CD，AD=BC，AC和BD交于点M，
那么图中全等三角形有 （ ）
A、2对 B、3对 C、4对 D、5对
 |
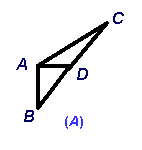
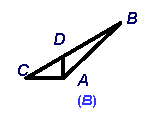
10、下列各组图形中，哪一组图形中AD是△ABC 的高( )
 | |||||
 |  | ||||
 | |||||||||
| |||||||||
 |
|
| |||||||
11*、与图1所示图形不全等的图形是 ( )
(图1) A B C D
三、画一画：（9分）
1、利用尺规，用三种不同的方法作一个三角形与已知直角三角形ABC全等，并简要说明理由。（同种理由视为是同一种方法）
四、證明解答題：（21分）
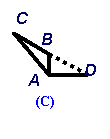
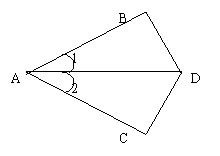
1、如图，图中的两个三角形全等，A和B，C和D是对应顶点。
（1） 用符号表示两个三角形全等。
（2） 写出它们的对应角、对应边。
（3） 用等号表示各对应角，对应边之间的关系。
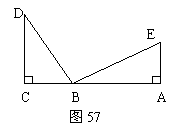2、已知：如图57，DC⊥CA，EA⊥CA，
CD=AB，CB=AE
求证：△BCD≌△EAB
证明：∵DC⊥CA，EA⊥CA (已知)
∴∠C=∠A=90° (垂直定义)
在△BCD与△EAB中
CD=AB
(已知)
∠C= （已证）
CB= （已知）
∴△BCD≌△EAB ( )
3、如图，已知DB⊥AB，DC⊥AC，B，C分别为垂足，DB=DC。
求证：DA平分∠BDC。（5分）
 |
4如图，有两个长度相同的滑梯，左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，（5分）
(1)两个滑梯的倾斜角∠ABC和∠DFE大小有什么关系？
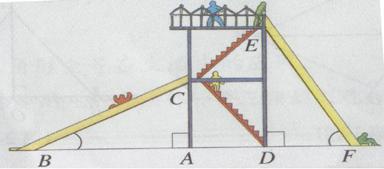(2)两个滑梯BC，EF所在的位置关系如何？