第四章《平面图形及其位置关系》
时间45分 满分100分 学号 姓名
 一、填空题(每小题1分,共6分)
一、填空题(每小题1分,共6分)
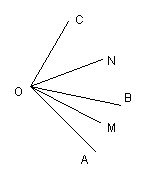
1.∠AOB=450,∠BOC=300,则∠AOC=_______0.
2.如图1所示,OM平分∠AOB,ON平分∠BOC,已知∠AOB<∠BOC,
那么可以确定∠AOM _______∠CON.(填">"、"=" 或"<"=
3.如图1所示,OM平分∠AOB,ON平分∠BOC,
已知∠AOC=1000,那么,∠MON=_______0. 图1
 4.如图2所示,用刻度尺测量图中线段的长度.AC=_______cm,BC=_______cm,AB=_______cm.最长的线段是_______,BC+AC_______AB(填">" 、"<"或"=").
4.如图2所示,用刻度尺测量图中线段的长度.AC=_______cm,BC=_______cm,AB=_______cm.最长的线段是_______,BC+AC_______AB(填">" 、"<"或"=").
5. 时针从2点到10分走到2点35分,它的分针转了______度.
6. 角平分线上任一点向两边垂线段的长______(填"不相等、相等")
7.把线段向一个方向延长,得到的是______;把线段向两个方向延长,
得到的是_____. 图2
8.在时钟上,从早晨8:00到晚上8:00时针转过_____0,分针转过_____0,秒针转过_____0.
二、选择题(每小题1分,共4分)
1. 若M是AB的中点,C是MB上任意一点,那么与MC相等的是( ).
(A)![]() (AC-BC)
(B)
(AC-BC)
(B)![]() (AC+BC)
(C)AC-
(AC+BC)
(C)AC-![]() BC (D)BC-
BC (D)BC-![]()
2.下列关于中点的说法,正确的是( ).
(A)如果MA=MB,那么点M是线段AB的中点 (B)如果MA=AB,那么点M是线段AB的中点
(C)如果AB=2AM,那么点M是线段AB的中点
(D)如果M是AB内的一点,并且MA=MB,那么点M是线段AB的中点
3.关于两点之间的距离,下列说法不正确的是( ).
(A)连结两点的线段就是两点之间的距离
(B)连结两点的线段的长度,是两点之间的距离
(C)如果线段AB=AC,那么点A到点B的距离等于点A到点C的距离
(D)两点之间的距离是连接这两点的所有的线的长度中,长度最短的
4.下列说法正确的是( ).
(A)平角就是一条直线 (B)周角就是一条射线
(C)平角的两条边在同一条直线上 (D)周角的终边与始边重合,所以周角的度数是00
5.在一个三角形中( ).
(A)一定有一个角等于600 (B)一定有一个角大于600
(C)一定有一个角小于600 (D)至少有一个角不小于600
6. 已知∠AOC=1350,OB为∠AOC内部的一条射线,且∠BOC=900,以OB为一条边,以OA为角平分线的角的另一边是( )
(A)∠BOC的平分线 (B)射线OC(C)射线OC的反向延长线(D)射线OC的反向延长线
三、解答题(每小题1分,共4分)
1. 如图3,把正方形ABCD对折,折痕为MN.把顶点D折到MN上的一点P上,折痕为CE,再把
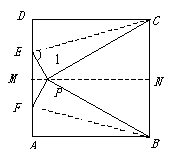 顶点A折到MN上的同一点,折痕为BF,请回答下列问题:
顶点A折到MN上的同一点,折痕为BF,请回答下列问题:
(1)线段PC、PB与正方形的边长有什么关系?
(2)∠CPB的度数是多少?
图3
(3)还能知道哪些角的度数?请指出来.
2. 观察下列图形,并阅读相关文字.
2条直线相交 3条直线相交 4条直线相交 5条直线相交
有2对对顶角 有6对对顶角 有12对对顶角 有20对对顶角
通过阅读分析上面的材料,计算后得出规律,当n条直线相交于一点时,有多少对对顶角出现?(n大于2的整数)
3. 科学知识是用来为人类服务的,所以学了科学知识,就要把知识运用我们的生活中,下面是用科学知识的两个事例:
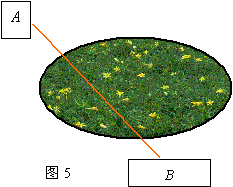 (1)如图5所示,从教学楼口A到图书馆B,个别同学不走人行道而穿过草坪,这是为什么?请你用学过的知识说明这个问题.
(1)如图5所示,从教学楼口A到图书馆B,个别同学不走人行道而穿过草坪,这是为什么?请你用学过的知识说明这个问题.
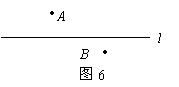
(2)如图6,A、B是河流L两旁的村庄.现在,要在河边修一个引水站向两村供水,引水站修在什么地方才能使所需管道最短?请在图中用点P标出引水站的位置,并说明理由.
 |
(3)结合上面两个事例,请你谈一谈,当把所学的知识用于生活中时,应该注意什么?
4. 怎样才能保证一队同学站成一条直线?
 5.
用刻度尺找出如图中四边形ABCD各边中点E,F,G,H,再依次把它们连结起来,借助量角器等工具找一找,其中有平行直线吗?若有,是哪几对?
5.
用刻度尺找出如图中四边形ABCD各边中点E,F,G,H,再依次把它们连结起来,借助量角器等工具找一找,其中有平行直线吗?若有,是哪几对?
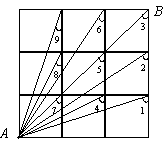 6. 下图是一个3×3的"网格型"正方形示意图,其中标注于∠1,∠2,∠3……∠9共九个角,你能用一种巧妙的方法迅速求出这九个角的和吗?说出来和同学们交流.
6. 下图是一个3×3的"网格型"正方形示意图,其中标注于∠1,∠2,∠3……∠9共九个角,你能用一种巧妙的方法迅速求出这九个角的和吗?说出来和同学们交流.
7. 阅读下面文字,完成题目中的问题
阅读材料:①平面上没有直线时,整个平面是1部分;②当平面上画出一条直线时,就把平面分成2部分;③当平面上有两条直线时,最多把平面分成4部分;④当平面上有三条直线时,最多可以把平面分成7部分;…
完成下面问题:
(1)根据上述事实填写下列表格
| 平面上直线的条数 | 0 | 1 | 2 | 3 | … |
| 平面被分成几部分 | … |
(2)观察上表中平面被分成的部分,他们的差是否有规律?如果有请你说出来.
(3)平面被分成的部分也有规律,请你根据(2)中的结论说出"平面被分成几部分"的规律.
(4)一块蛋糕要分给10位小朋友,你至少要切几刀?
参考答案
一、填空题
1. 150或750;2. <;3. 50;4. 略,略,略,AB,>;5. 150;6. 相等;7. (射线,直线);8. 360,4320,259200;
二、选择题
1. A;2. D;3. A;4. C;5. D;6. D
三、解答题(每小题1分,共4分)
1. (1)相等;(2)600.
2. n(n-1)
3. (1)提示:两点之间,线段最短;(2) 略;(3)各抒己见吧!
4. 本题为开放问题,答案不唯一,只要可行即为正确.现提供一种答案,仅供参考:先让两个同学站好不动,其他同学依次往后站,要求只能看到各自前面的那个同学.
5. 有,2对.
6. 除∠3=∠5=∠7=450外,其它各角的具体变数不易求得,可用如下办法:由于沿AB作对折时,上下图形能够重合,恰有∠1+∠9=∠2+∠6=∠4+∠8=900,故九个角和为3×900+3×450=4050.
7. (1)1,2,4,7,…;(2)有规律,个数上差依次为1,2,3,…(3)当有n条直线时,平面被分成(1+1+2+3+…+n)部分,即[n(n+1)+1]部分;(4)4刀