第三章达标测验题
(时间100分钟 满分100分)
一、选择题:(每小题3分,共30分)
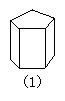
1.如图1所示的棱柱有( )
A.4个面 B.6个面 C.12条棱 D.15条棱
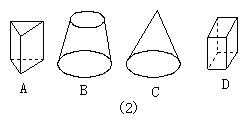
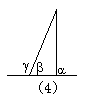
2.如图2,从正面看可看到△的是( )
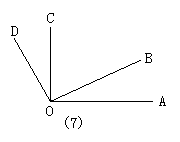
3.如图3,图中有( )
A.3条直线 B.3条射线 C.3条线段 D.以上都不对
4.下列语句正确的是( )
A.如果PA=PB,那么P是线段AB的中点; B.作∠AOB的平分线CD
C.连接A、B两点得直线AB; D.反向延长射线OP(O为端点)
5.如图4,比较∠α、∠β、∠γ 的大小得( )
A. ∠γ>∠β>∠α;B. ∠α=∠β;C. ∠γ>∠α>∠β;D. ∠β>∠α>∠γ.
6.5点整时,时钟上时针与分钟之间的夹角是( )
A.210° B.30° C.150° D.60°
7.两个角,它们的比是6:4,其差为36°,则这两个角的关系是( )
A.互余 B.互补 C.既不互余也不互补 D.不确定
8.∠α=40.4°,∠β=40°4′,则∠α与∠β的关系是( )
A. ∠α=∠β;B. ∠α>∠β;C. ∠α<∠β;D. 以上都不对
9.如果∠α=3∠β, ∠α=2∠θ,则必有( )
A. ∠β=
∠θ;B.∠β=
∠θ;C.∠β=
∠θ;D.∠β=
∠θ;
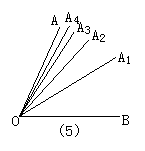
10.如图5所示,已知∠AOB=64°,OA1平分∠AOB,OA2平分∠AOA1,OA3 平分∠AOA2,OA4平分∠AOA3,则∠AOA4的大小为( )
A.8° B.4° C.2° D.1°
二、填空题:(每小题3分,共30分)
11.已知线段AB=8cm,延长AB至C,使AC=2AB,D是AB中点,则线段CD=______.
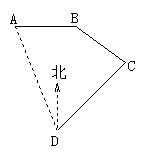
12.如图,从城市A到城市B有三种不同的交通工作:汽车、火车、飞机,除去速度因素,坐飞机的时间最短是因为___________.
13.57.32°=_______°_______′_______″;27°14′24″=_____°.
14.已知∠a=36°42′15″,那么∠a的余角等于________.
15.∠1+∠2=180°,∠2+∠3=180°,根据________,得∠1=∠3.
16.表示O点南偏东15°方向和北偏东25°方向的两条射线组成的角等于____
17.如图,∠AOC=90°,∠AOB=∠COD,则∠BOD=______°.
18.102°43′32″+77°16′28″=________;98°12′25″÷5=_____.
19.已知线段AB=acm,点A1平分AB,A2平分AA1,A3平分AA2,……, 
平分
, 则
=_______________cm.
20.在平面上有任意四点,过其中任意两点画直线,能画_______条直线.
三、解答题:(21、24、25、26每题6分,22、23题每题8分)
21.根据下列语句画图:
(1)画∠AOB=120°;(2)画∠AOB的角平分线OC;
(3)反向延长OC得射线OD;
(4)分别在射线OA、OB、OD上画线段OE=OF=OG=2cm;
(5)连接EF、EG、FG;
(6)你能发现EF、EG、FG有什么关系?∠EFG、∠EGF、∠GEF有什么关系?
22.已知线段AB=10cm,直线AB上有一点C ,且BC=4cm,M是线段AC的中点,求AM 的长.
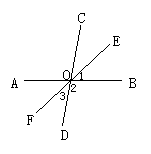
23.如图,直线AB、CD交于O点,且∠BOC=80°,OE平分∠BOC,OF为OE 的反向延长线.
(1)求∠2和∠3的度数.
(2)OF平分∠AOD吗?为什么?
24.一个角的补角与它的余角的度数之比是3:1,求这个角的度数.
25.测量员沿着一块地的周围测绘.从A向东走600米到B,再从B向东南(∠ABC= 135°)走500米到C,再从C向西南(∠BCD=90°)走800米到D.用1厘米代表100米画图, 求DA的长(精确到10米)和DA的方向(精确到1°).
26.利用线段、角、三角形、圆等图形为你的学校设计一个校标,并简述你的设计思路.
答案:
一、选择题
1.D 2.C 3.C 4.D 5.C 6.C 7.B 8.B 9.C 10.B
二、填空题
11.12cm 12.两点之间,线段最短 13.57、19、12;27.24
14. 53°17′45″ 15.同角的补角相等
16.140° 17.90 18.180°;19°38′29″. 19. 
a 20.1或4或6
三、解答题
21.(6)EF=EG=FG,∠EFG=∠EGF=∠FEG=60°
22.AM=7cm或3cm
23.(1)∠2=100°,∠3=40°;(2)∠AOF=40°,OF平分∠AOD
24.设这个角为x0,( 180-x):(90-x)=3:1,x=45.