八年级数学第二学期教学目标检测题
八年级数学科 之五
| 题号 （分值） | 一 （40） | 二 （40） | 三 （40） | 合计 （120） |
| 得分 |
|
|
|
|
检测范围：第十九章 四边形 完卷时间：45分钟 满分：120分
一、
|
|
1、如图，已知AD∥BC，要使四边形ABCD为平行，
|
|
四边形需要增加一个条件是：_______。
2、矩形的对角线长是10cm，一边长是6cm，则其周长是_____cm，
|
|
面积是_____cm2。
| ||||
 | ||||
|
|
3、如图，在△ABC中，D、E分别是AB、AC的中点，
 |
则DE与 BC的位置关系是：________，DE与 BC的数量关系是：________。
4、若菱形的周长为24 cm，一个内角为60°，则菱形的面积为______ cm2。
5、对角线长为10 cm的正方形的边长是______cm，面积是______ cm2。
6、矩形的两条对角线的夹角为60°，一条对角线与短边的和为15 cm ，则短边
的边长为______ cm。
7、若梯形的上底长为3 cm，中位线长为4 cm， 则它的下底长为______cm。
|
|
 |
|
|
二、
选择题。（每小题5分，共40分）
9、对角线互相垂直平分的四边形是 （ ）
A、平行四边形 B、矩形 C、菱形 D、梯形
1
10、如图，点D、E、F分别是△ABC的三边的中点，连结DE，EF，DF，则
|
图中共有平行四边形的个数是
（ ）
|
|
A、2 B、3 C、4 D、5
11、能够判定一个四边形是平行四边形的条件是 （ ）
A、一组对角相等 B、两条对角线互相平分
C、两条对角线互相垂直 D、一对邻角的和为180°
12、菱形具有而矩形不一定具有的性质是 （ ）
A、对角相等且互补 B、对角线互相平分
|
C、对角线互相垂直 D、一组对边平行，另一组对边相等
13、下列性质正方形具有而菱形不具有的是 （ ）
A、四条边相等 B、对角线互相垂直平分
C、对角线相等 D、对角线平分一组对角
14、矩形的面积为120cm2，周长为46cm，则它的对角线长为 （ ）
A、15cm B、16cm C、17cm D、18cm
15、如图，等腰梯形ABCDK中，AD∥BC， AD=5，AB=6，
|
|
BC=8，AE∥DC，则△ABE的周长是
（ ）
|
|
A、3 B、12 C、15 D、19
|
16、下列说法错误的是 （ ）
A、三角形的重心一定在三角形内 B、正方形的重心是它的两条对角线交点
C、一个多边形只有一个重心 D、过三角形重心的一条直线平分三角形的面积
2
三、 解答题。（每小题10分，共40分）
17、如图，在△ABC中，AB=AC， AD⊥BC于D， BC=12，AD=8，E是AB的中点，求DE的长。
 | |||
| |||
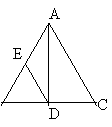18、如图， ABCD中，AB=3，BC=4，AC=5，求证： ABCD是矩形。
| ||||||||
| ||||||||
|
| |||||||
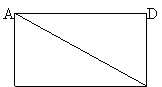
3
19、如图，AD是△ABC的角平分线，DE∥AC交AB于E，DF∥AB交AC于F，判断四边形AEDF的形式状，并说明理由。
 | |||
| |||
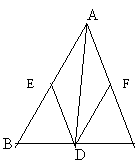20、如图，在梯形ABCD中，AD∥BC， AB=DC，BD⊥DC，且BD平分∠ABC。若梯形的周长为20cm，求此梯形的中位线长。
 | ||||||
|
| |||||
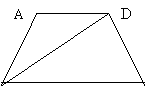4