八年级数学第二学期期末检测试卷
（100分钟完成，满分100+20分）
一、 填空题（每小题3分，满分42分）
1. 一次函数y=2x–3的截距是__________.
2. 写出一个图象不经过第三象限的一次函数：________________．
3. 方程x2–2x=0的根是_________________.
4.
如果关于x的方程x2＋x+
=0有两个不相等的实数根, 那么k的取值范围是______.
5. 如果一元二次方程x2＋4 x－m = 0的一个根为1, 那么另一个根为______.
6.
以
、
为根, 且二次项系数为1的一元二次方程是__________________.
7. 二次函数y=–3x2+5x–6的图象的开口方向是_______________.
8. 二次函数y=–2x2的图象向右平移3个单位后得到的图象所表示的二次函数解析式是______________.
9. 到A、B两点距离相等的点的轨迹是________________________________.
10.
点A(2,
)与点B(–1,0)之间的距离是5, 那么的值为___________.
11. 已知弓形的半径为13, 高为1, 那么弓形的弦长为______________.
12. 梯形的上底长为5, 下底长为9, 那么它的中位线长为_____________.
13. 已知□ABCD的面积为10cm2, 点E是CD边上任意一点，那么△ABE的面积是__________ cm2.
14. 如果菱形的一个内角为120º, 较短的对角线为4, 那么这个菱形的面积是_________.
二、 选择题（每小题3分，满分12分）【每小题只有一个正确答案,将代号填入括号内】
15. 下列方程中，满足两个实数根的和为2的方程是…………………………… ( )
（A）2x2 – 4=0； （B）2x2–4x–1=0； （C）x2–2x+2=0； （D）x2+2 x-2 =0．
16. 函数
（常数
）的图象经过的象限为……………………………
( )
(A) 第一、二象限; (B) 第一、三象限; (C) 第二、四象限; (D) 第三、四象限．
17. 连结对角线垂直的四边形各边中点所得到的四边形是 ……………………… ( )
(A)
正方形; （B）菱形;
(C) 矩形; （D）等腰梯形.
18. 如图,在梯形ABCD中, AD//BC, AD : BC =1:2, 点E在AC上,
AE : EC=1 : 3, 那么S△ABE: S△BCE : S△ADC等于…… ( )
(A)1:2:2; (B)1:2:3; (C)1:3:2; (D) 1:3:3.
三、 简答题（每小题6分，共18分）
19.
解方程：x2 – 2 (
x-1) = 6.
20.
已知方程x2+3x-5=0的两根为
、
, 求
值.
21. 已知二次函数的图象经过点（0，–1）、（1，–3）、（–1，3），求这个二次函数的解析式.并用配方法求出图象的顶点坐标．
四、 解答题（每题7分，满分28分）
22. 某公司生产一种新产品，前期投资300万元，每生产1吨新产品还需其他投资0.3万元，如果生产这一产品的产量为x吨，每吨售价为0.5万元．
（1） 设生产新产品的总投资y1万元，试写出y1与x之间的函数关系式和定义域；
（2） 如果生产这一产品能盈利，且盈利为y2万元，求y2与x之间的函数关系式，并写出定义域；
（3） 请问当这一产品的产量为1800吨时，该公司的盈利为几万元？
23. 如图，在梯形ABCD中，AD//BC，AB=DC，点E在BC的延长线上，DE=DB．
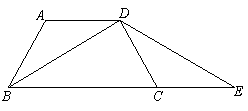求证：AD=CE．
24.
已知二次函数的解析式为
（
为常数）．
（１） 求证：这个二次函数图象与
轴必有公共点；
（２） 设这个二次函数图象与
轴相交于A、B两点（点A在点B的左侧），与
轴相交于点C．当BC=
时，求的值．
25.
如图所示，正方形网格中的每个小正方形边长都是1，画出一个周长为5
三角形,且使它的每个顶点都在小正方形的顶点上.判断你所画三角形的形状,并说明理由.
附加题（供学有余力的学生选做，每题10分，满分20分）
1．依法纳税是每个公民应尽的义务，国家规定个人工资、薪金所得税的征收方法如下：
①个人税前月工资、薪金1000元及以下免缴个人所得税；
②个人税前月工资、薪金超过1000元的部分按以下不同的税率征税，超过部分：
在500元及以内的这一部分按5%税率征税；
在500元到2000元之间的这一部分按10%税率征税；
在2000元到5000元之间的这一部分按15%税率征税；
在5000元到20000元之间的这一部分按20%税率征税；
……
（以上各段数据中均含最大值，不含最小值）
根据上述信息，解决下列问题：
（1） 如果某人的月工资、薪金为2500元，那么他应缴纳的个人所得税为多少元？
（2） 如果某单位职工的税前月工资、薪金都在3000元到6000元之间，设某一职工的税前月工资、薪金为元，应缴纳的个人所得税为
元．求与之间的函数解析式，并写出它的定义域．
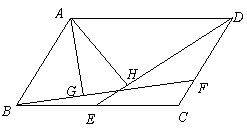2．如图，在□ABCD中，点E、F分别在BC、CD边上，BF=DE，AG⊥BF，AH⊥DE，垂足分别为G、H．求证：AG=AH．
参考答案及评分意见
一、 填空题（本题满分４2分）
1．–3； 2．
； 3．
0, 
2； 4．
； 5.–5 ； 6．
； 7．向下； 8．
； 9．线段AB的垂直平分线；
10．
； 11. 10; 12. 7;
13. 5; 14. 
.
二、 选择题（每小题3分，共12分）
15. B; 16. A; 17. C; 18. C.
三、 简答题（每小题６分，共18分）
19. 解: 
， ………(1分) △=
，…… (2分)
，…………(2分) 
．………… (1分)
20.解: x1+x2=–3, x1x2=
,…… (1+1分) 
……… (1分)
……(1分) =
…… (1分) =
.……（1分）
21.解:（1）设二次函数的解析式为
， …………………（1分）
由题意得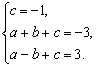
……（2分） 解得
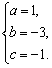……………（1分）
∴二次函数的解析式为
……………………………………（1分）
，∴顶点坐标为
，
．……（1分）
四、解答题（每小题7分，共28分）
22. 解:（1） 
, ……… (1分) 定义域为
………… (1分)
（2）
，……(1分) 
．………(1分)
定义域为
………（1分）
（3）
，
．………………………(1分)
∴当这一产品的产量为1800吨时，该公司的盈利为60万元．……(1分)
23. 证法一：在梯形ABCD中，∵AD//BC，AB=AC，
∴∠ABC=∠DCB（等腰梯形同一底上的内角相等），…………（1分）
∠A+∠ABC=180°．……………………………………………（1分）
又∵∠DCE+∠DCB=180°，∴∠A=∠DCE．…………………（1分）
∵DB=BE, ∴∠DBC=∠E. ………………………………………（1分）
∵∠ADB=∠DBC，∴∠ADC=∠E．……………………………（1分）
∴△ABD≌△CDE（AAS）． ……………………………………（1分）
∴AD=CE． ………………………………………………………（1分）
证法二：连结AC，…………………………………………………………………（1分）
在梯形ABCD中，∵AD//BC，AB=AC，
∴AC=BD（等腰梯形的对角线相等）．………………………………………（1分）
∠ABC=∠DCB（等腰梯形同一底上的内角相等）．…………………… （1分）
又∵BC=CB, ∴△ABC≌△DCB (SAS). ∴∠ACB=∠DBC. ………………（1分）
∵DB=BE, ∴∠DBC=∠E. ∴∠ACB=∠E.∴AC//DE. ……………………（1分）
又∵DE=BD，∴DE=AC．
∴四边形ACED是平行四边形（一组对边平行的四边形是平行四边形）． （1分）
∴AD=CE．（平行四边形的对边相等）． ……………………………………（1分）
24. （1）证明：∵
，……………（1分）
∴这个二次函数图象与轴必有公共点．…………………………（1分）
（2）解：当
时，
，
，
∴
. ………………………………………………（1分）
如果点A为 (1, 0), 那么点B
(
0). 而C（0，
）．
∵BC=，∴
，……………（1分）
∴
………………………………（1分）
如果点A为 ( 0),那么点 B为 (1,
0).而C（0，）．
，
．……（1分）
……………………………………（1分）
∴的值为4或
．
25. 解:如图,△ABC（或△A’B’C’等）就是所求的三角形. ……（4分）
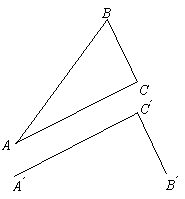△ABC是直角三角形.……（1分）
∵AB=5,AC=
,BC=
.（1分）
∴AC 2 +BC 2 =
,
AB 2 =52 =25,
∴AC 2 +BC 2 =AB 2. ……（1分）
∴△ABC是直角三角形.
附加题（供学有余力的学生选做，每题10分，满分20分）
1. 解：（1）纳税部分：2500-1000=1500（元），…………………………………（1分）
应缴纳的个人所得税为500×5%+（1500–500）×10%=125（元）．（2分）
（2）
，…（4分）
25+150+
，
，定义域为3000<x≤6000。…………………………（3分）
2．证明：连结AE、AF，……………………………………………………………（1分）
设△AED的AD边上的高为
．
∵
，S□ABCD 
，……………………………………（2分）
∴
=
S□ABCD ．……………………………………………………（１分）
同理：
= S□ABCD ． ∴ ．………………………（2分）
∵AG⊥BF，AH⊥DE，
∴
AH，=
．………………………………（1分）
∴
．…………………………………………………（1分）
∵BF=DE，∴AG=AH．………………………………………………………（1分）