苏州市中学2003-2004学年第　一　学　期期末考试

初二数学试卷

班级　　　　学号　　　　姓名　　　　　　 

说明：本试卷共四大题，25小题，满分100分，考试时间100分钟。

一、选择题（本大题共8小题，每小题3分，共24分。在每小题给出的四个选项中，只有一项是正确的，把正确选项前的字母填在下面的表格内。）

1．下列各式中，正确的是

A．y³·y²=y⁶  B．(a³)³=a⁶　　　C．(－x²)³=－x⁶ D．－(－m²)⁴=m⁸

2.计算(x－3y)(x+3y)的结果是

A.x²－3y²　　　　　B.x²－6y²  C. x²－9y²D.2x²－6y²

3.矩形和菱形都具有的特征是

A．对角线相等　　　　　　　  B．对角线互相平分

C．对角线互相垂直　　　　　  D．对角线平分一组对角

4．若a>b，则下列各式中成立的是

A．－3a>－3b　　　　　　　 B．　　　　C．a－3>b－3　　　　　 D．2a+3<2b+3

5.粉笔盒里共有四支一样的粉笔，其中，三支是白色的，一支是红色的，老师随手从粉笔盒 中拿出一支粉笔，恰好是红色的那支的可能性是

A．100%　　　　　　  B．75%　　　　　　　 C．50%　　　　 D．25%

6．下列各式中成立的是

A． x²y²=(x+y)(x－y )　　　　　 

B．1－x²=(1－x)²

C.(x²+4)（－4x）=(x－2)²　　　

D．x²－

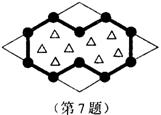
7.如图，菱形花坛的边长为6cm，一个内角为60℃，在花坛中用花盆围出两个正六边形的图形（图中粗线部分），则围出的图形的周长为

A．20cm　　　　　　　 B．22cm　　

C．24cm　　　　　　　 D．以上都不对

8.如果某种彩票的中奖机会是25%，则下列说法中正确的是

A．买100张这各彩票，就会中奖25次奖　 B．买25张这种彩票，就会中1次奖

C．买4张这种彩票，就会中1次奖　　 D．每买4张这种彩票，就可能中1次奖

二．填空题（本题共8小题，每小题3分，共24分，把答案填在题中横线上。）

9．计算：3x²y·(－2xy³)=__________________.　　　　　　　　　　　　　　　　　

10.计算：（3x－1）(2x+1)=________________.

11.等腰梯形的____________ 相等。（写出一个正确结论即可）

12.不等式3（1－x）≤2x的解集是________________。

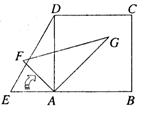
13.如图，已知正方形 ABCD,E是BA延长上的点，且∠E=60°，现将△ADE绕点A顺时方向旋转到△AGF的位置，则当旋转角度∠EAF=_____________时，FG∥AB。

14.多项式x²+2mx+64是完全平方式，则m=_____________。

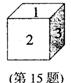
15.如图，若在1，2，3，4这四个数字中，选择六个恰当的数字（可以重复选取），分别标在一个均匀的正方体骰子的6个面上，若要使得投掷骰子时，

“1”朝上的可能性为，则这个正方体的6个面上的数学可以是_____________。（填上一组你认为正确的6个数学）

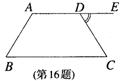
16.如图，在等腰梯形ABCD中，延长AD到E，若∠B=58 °，

则∠EDC=________。

三、解答题（本大题共8小题，共52分，解答应写出必要的计算过程、推演步骤或文字说明。）

17．（本题5分）计算：(2x+y)(2x－y)+(x+y)².

18. （本题5分）已知，y₁=x－3, y₂=，当x取何值时，y₁<y₂?

19．（本题6分）解不等式组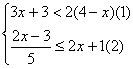，并把它的解集表示在数轴上。

20．（本题9分）因式分解：

（1）a²m+2am+m　　　　　 　　　　　　　　　 (2)2(2－x)－x(x－2)

(3)a⁴－16b⁴

21.(本题6分)

　现有如图所示的6种基本图案，请选择其中的2种图案，用铅笔填入图1的四个小方格中，设计出一个瓷砖图案。然后，再将你设计的瓷砖图案通过轴对称，用铅笔填入图2，从而设计出更加美丽的大型图案。

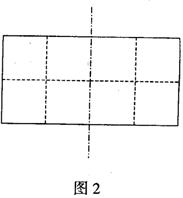
通过轴对称得（图中长虚线为对称轴）；

22．（本题7分）

如图，已知等边△ABC和等边△DBC有公共的底边BC。

（1）以图1中的某个点为旋转中心，旋转△DBC，就能使△DBC与△ABC重合，则满足题意的点为____________________；（写出所有的这种点）

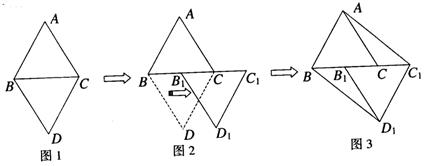（2）如图2，已知B₁是BC的中点，现沿着由点B到点B₁的方向，将△DBC平移到△D₁B₁C₁的位置。请你判断：得到的四边形ABD₁C₁是平行四边形吗？说明你的理由。

23．（本题7分）

小华家是我市第一批9万户统一换装“峰谷分时”电表的家庭之一，他们家将率先享受苏州市生活用电“峰谷分时电价”的新政策，用电价将按不同时段实行不同的价格，具体为：8点至21点为“峰时”，电价为每千瓦时0.55元；21点至次日8点为“谷时”，电价为每千瓦时0.30元，而我市原来实行的电价为每千瓦时0.52元。

（1）小华估计了一下，自己家大约平均每月用电100千瓦时，其中“峰时”用电约占80%，请你帮小华算一下，他家原来平均每月需交电费多少元？实现“峰谷分时电价”后，他家的电费会下降吗？若下降，下降多少元？

（2）小华希望在用电量不改变的前提下，改变原来的用电习惯，使他家平均每月的电费能够下降8～12元。假设小华家今后“峰时”用电占整个家庭用电的x%，那么，x在什么范围时，才能达到小华的期望？

24．（本题7分）

右图是两个可自由转动的转盘，其中转盘A的蓝色部分占，转盘B的蓝色部分占。转动转盘，转盘停止后指针所指的颜色就是转出的颜色，现在，甲、乙两个做下列游戏：

（1）甲转动A盘，乙转动B盘，每人转动十次，谁转出红色的次数多谁就获胜，你认为这个游戏规则对双方公平吗？如果不公平，谁容易获胜？请说明理由。

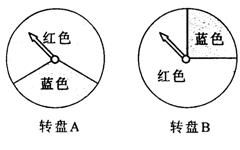（2）小明提出了下面的改进方案：由第三个人来先后转动上面的两个转盘，如果两个转盘都转出红色，则甲赢，否则乙赢。小明准备做一些实验来研究这种方案是否公平。请你帮小明设计一种替代实验的方法，并写出实验的步聚。

四、附加题（本题如果解答正确，加6分，但全卷总分不超过100分）

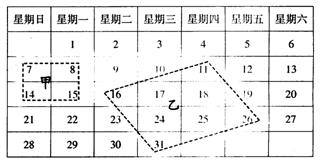
25．如图是2003年12月份的日历牌，我们在日历牌中用两种不同的方式选择四个数。

（1）从甲种选择构成的“矩形”中发现14×8－7×15=7，即对角线上两数积的差为7。请你平移矩形甲，使它的四个顶点落在其他的四个数上，对角线上的两数积的差还为7吗？

（2）对乙种选择构成的“平行四边形”顶点处的四个数字，按上述方法计算和平移，你又能得出什么结论？

（3）由第（1）、（2）小题得出的这些规律是否具有一般性？如果你认为不具有一般性，请举反例；如果你认为具有一般性，请假设所选择的某个数为n，然后通过含n的代数式的运算加以说明。