人教实验版八年级(上)数学单元目标检测题(三)
(一次函数)
班级 姓名 号次
一.选择题( 本大题共8小题, 每小题4分,共32分)
1.判断下列变化过程中,两变量存在函数关系的是( )
A.![]() 是变量,
是变量,![]() B.人的身高与年龄
B.人的身高与年龄
C.三角形的底边长与面积 D.速度一定的汽车所行驶的路程与时间.
2.下列函数关系式:①![]() ;②
;②![]() ③
③![]() ;④
;④![]() .其中一次函数的个数是( )
.其中一次函数的个数是( )
A. 1个 B.2个 C.3个 D.4个
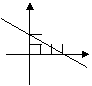
 3.在直角坐标系中,既是正比例函数
3.在直角坐标系中,既是正比例函数![]() ,又是
,又是![]() 的值随
的值随![]() 值的增大而减小的图像是( )
值的增大而减小的图像是( )
 A
B
C
D
A
B
C
D
4.如图,直线![]() 经过A(0,2)和B(3,0)两点,那么
经过A(0,2)和B(3,0)两点,那么
这个一次函数关系式是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.大伯出去散步,从家走了20分钟,到一个离家900米的阅报亭,看了10分钟报纸后,用了15分钟返回到家,下面哪个图形表示张大伯离家时间与距离之间的关系( ):
6.要从![]() 的图象得到直线
的图象得到直线![]() ,就要将直线
,就要将直线![]() ( )
( )
A.向上平移 ![]() 个单位 B. 向下平移
个单位 B. 向下平移 ![]() 个单位
个单位
C. 向上平移 2个单位 D. 向下平移 2个单位
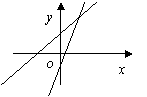 7.如图一次函数
7.如图一次函数![]() 和
和![]() 在同一坐标系内的图象,则
在同一坐标系内的图象,则![]() 的解
的解![]() 中( )
中( )
A.m>0,n>0 B.m>0,n<0 C. m<0,n>0 D.m<0,n<0
8.图1是水滴进玻璃容器的示意图(滴水速度不变),图2是容器中水高度随滴水时间变化的图像.
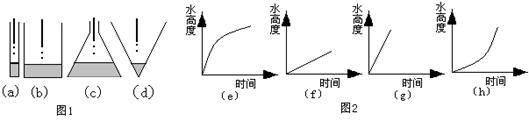
给出下列对应:
(1):(a)——(e) (2):(b)——(f) (3):(c)——h (4):(d)——(g)其中正确的是( )
(A)(1)和(2) (B)(2)和(3) (C)(1)和(3) (D)(3)和(4)
二. 填空题(本大题共8小题,每题4分共32分)
1. 如果函数![]() ,那么
,那么![]() ________
________
2.小明将RMB1000元存入银行,年利率为2%,利息税为20%,那么![]() 年后的本息和(扣除利息税)
年后的本息和(扣除利息税)![]() (元)与年数
(元)与年数![]() 的函数关系式是
.
的函数关系式是
.
3.已知一次函数![]() +3,则
+3,则![]() = .
= .
 4.已知一次函数
4.已知一次函数![]() ,函数
,函数![]() 的值随
的值随![]() 值的增大而增大,则
值的增大而增大,则![]() 的取值范围是 .
的取值范围是 .
5.已知一次函数y=2x+4的图像经过点(m,8),则m=________。
6.已知直线![]() 与
与![]() 轴,
轴,![]() 轴围成一个三角形,则这个三角形面积为 (平方单位).
轴围成一个三角形,则这个三角形面积为 (平方单位).
7.若一次函数y=kx+b的图像经过(-2,-1)和点(1,2),则这个函数的图像不经过 象限 .
 8. 根据下图所示的程序计算函数值,若输入的x值为
8. 根据下图所示的程序计算函数值,若输入的x值为![]() ,则输出的结果为
,则输出的结果为
三.解答题(本大题共4小题,共36分)
1. 在某地,人们发现某种蟋蟀1分钟所叫次数与当地温度之间近似为一次函数关系。下面是蟋蟀所叫次数与温度变化情况对照表:
| 蟋蟀叫次数 | … | 84 | 98 | 119 | … |
| 温度(℃) | … | 15 | 17 | 20 | … |
(1)根据表中数据确定该一次函数的关系式;
(2)如果蟋蟀1分钟叫了63次,那么该地当时的温度大约为多少摄氏度?
2.某公司到果园基地购买某种优质水果,慰问医务工作者,果园基地对购买量在3000千克以上(含3000千克)的有两种销售方案,甲方案:每千克9元,由基地送货上门。乙方案:每千克8元,由顾客自己租车运回,已知该公司租车从基地到公司的运输费为5000元。
(1)分别写出该公司两种购买方案的付款![]() (元)与所购买的水果质量
(元)与所购买的水果质量![]() (千克)之间的函数关系式,并写出自变量
(千克)之间的函数关系式,并写出自变量![]() 的取值范围。
的取值范围。
(2)依据购买量判断,选择哪种购买方案付款最少?并说明理由。
3.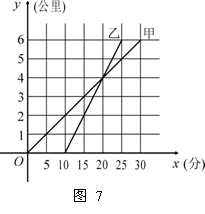 甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图7. 根据图象解决下列问题:
甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图7. 根据图象解决下列问题:
(1) 谁先出发?先出发多少时间?谁先到达终点?先到多少时间?
(2) 分别求出甲、乙两人的行驶速度;
(3) 在什么时间段内,两人均行驶在途中(不包括起点和终点)?在这一时间段内,请你根据下列情形,分别列出关于行驶时间x的方程或不等式(不化简,也不求解):① 甲在乙的前面;② 甲与乙相遇;③ 甲在乙后面.
4. 阅读:我们知道,在数轴x=1表示一个点,而在平面直角坐标系中x=1表示一条直线;我们还知道,以二元一次方程2 x – y + 1 = 0的所有解为坐标的点组成的图形就是一次函数y = 2 x - 1的图象,它也是一条直线如图①。
观察图①可以解出,直线x=1现直线y = 2 x -1的交点P的坐标(1,3),就是方程组![]() 的解,所以这个方程组的解为
的解,所以这个方程组的解为
![]()
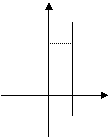
 在直角坐标系中,x≤1表示一个平面区域,即直线x = 1以及它左侧的部分,如图②;y≤2 x + 1也表示一个平面区域,即直线y = 2 x+1以及它下方的部分,如图③。
在直角坐标系中,x≤1表示一个平面区域,即直线x = 1以及它左侧的部分,如图②;y≤2 x + 1也表示一个平面区域,即直线y = 2 x+1以及它下方的部分,如图③。
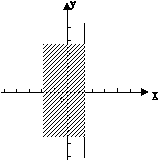

(1,3)
O 1 x 1
(图①) (图②) (图③)
 回答下列问题:
回答下列问题:
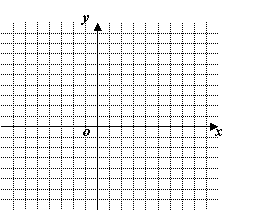
(1)在直角坐标系(图④)中,用作图象的方法求出方程组![]() 的解;
的解;
(2)用阴影表示 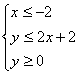 所围成的区域。
所围成的区域。
评价三答案
一、DBCBD AAB 二、1、3 2、y=1000+16x 3、-1 4、m〈-2,5、2 6 、18
7、第四 8、![]()
三、1(1)y=7x-121,(2)12 2(1)y甲=9x,y乙=8x+5000(2)当x〈5000时,选甲方案;当x=5000时,选甲、乙方案均可;当x〉5000时,选乙方案。3、(1)甲比乙早10分钟出发,乙比甲早5分钟到达,(2)V甲=0.2km/分 V乙=0.4km/分 (3)当10<t<25两人均在途中,(1) 10<t<20甲在乙前面,(2) t=20甲与乙相遇,(3) 20<t<25,甲在乙后面 4.(1) 通过图象法求得x=2,y=6 (2)略