八年级上期期末数学复习试卷

一、选择题:

1.要画一个面积为20cm²的长方形，其长为xcm，宽为ycm，在这一变化过程中，常量与变量分别为（　 ）

A.常量为20，变量为x,y;　　　　B.常量为20、y,变量为x;

C.常量为20、x,变量为y;　　　　D.常量为x、y，变量为20;

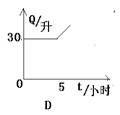
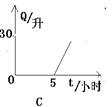
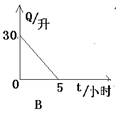
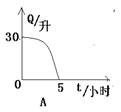2.油箱有油30升，每小时耗油6升，则油箱中剩余油量Q（升），与耗油时间t（小时）之间的关系式大致可表示为（　 ）

3.下列函数（其中x是自变量）中，不是正比例函数的个数有（　）

　 (1)y=-x; (2)y+2=2(x+1); (3) y=k²x(k是常数);(4)y²=x²

　 A.1个　　　B.2个　　  C.3个　　　 D.4个

4.若多项式4x³-2mx²-2x²+3 合并同类项后是三次二项式，则m满足的条件是（　 ）

A.m=-1　　　　B.m≠1　　　　  C.m=0　　　 D.m≠0

5.如果m-n=,那么-3(n-m)的值是（　 ）

A.-;　　B.;　 C.;　 D.;

6.下列各式计算正确的是（ ）

A.a+2b=3a² 　　B.a²a⁴=2a⁸ C.( -a²b³)²=a⁴b⁹D.a⁶÷a³=a³(a≠0)

7.用科学记数法表示0.00032,正确的是（ ）

A.3.2×10^-4 B.3.2×10^-3C.3.2×10^-5 D. 0.32×10^-2

8.点A（x，y₁）在函数y=2x的图象上，点B（x，y₂）在y=-x+3的图象上，若使y₁≥y₂则x的取值范围应为（　 ）
A.x≤3　　　　B.x≥3　　　 C.x≤1　　　 D.x≥1

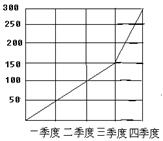
9.如图是某厂2004年各季度产值统计图（单位：万元），则下列说法正确的是（　 ）

A.四季度中，每季度生产总值有增有减;

 B.四季度中，前三季度生产总值增长较快;　　　　　　　　　　　　　　　  C.四季度中，各季度的生产总值变化一样;　　　　　　　　　　　　　　　　　　　　 D.第四季度生产总值增长最快.

10.如图，AB=AC，AE=AD，则（1）△ABD≌ △ ACE;

（2）△BOE ≌△COD;（3）△BDC≌ △CEB;（4）点O在∠BAC的平分线上，以上结论（ ）

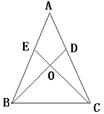　　 A.都正确　　　　B.都不正确　

　　 C.只有一个正确 D.只有一个不正确

 二.填空题:

1.　　 已知2y=x-6,则y与_____________{_}成正比例函数关系

2.　　 点（x,y）与点（x,-y）的关系是____________.

3.　　 (x-p)(x+2)展开整理后不含x项，则p的值为____________.

4.　　 如果4m²n+A=4mn(B+2n²),则A=_______B=_________.

5.　　 分解因式a(x-1)+(1-x)=__________.

6.　　 若x=1+y,则多项式x²-2xy+y²-3x+3y+2=____________.

7.　　 单项式42x²yz,6xy²z²的公因式是_______.

8.　　 计算：1999²-1998×2002=__________.

9.　　 k=_______,b=______时，一次函数y=kx+b和 y=bx-k交于点（5，13）.

10.  已知，一次函数y=1/2x+b的图象与坐标轴分别交于A（3，0），B（0，b），坐标原点为O，则以O，A，B为顶点的三角形的面积为________.

三.解答题

11.  计算：-3²+(-3)²+(-3)²-(-3³)+(-)¹⁹⁹⁹4²⁰⁰⁰.

12.  计算：(2x-y)(y+2x)-2(3x-2y)(-2y-3x)-(11x-3y)(2x-3y).

13.  已知:x²+4x+y²-10y+29=0,求的值.

14.  已知：(x+1)²+∣y-1∣=0 ，求2(xy-5xy²)-(3xy²-xy)的值.

15.  已知直线y=2x+1.

（1）求已知直线与y轴交点A的坐标.

（2）若直线y=kx+b与已知直线关于y 轴对称，求k与b.

16. 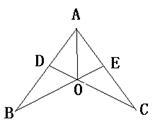 如图，CD⊥AB于点 D，BE⊥AC于点E，BE，CD交于点O，且AO平分∠BAC.

求证OB=OC.

17.  若a,b互为相反数，c,d互为倒数,m的绝对值为2,

求(a+b)(a-b)+(cd)^-1÷(1-2m+m²)的值.

18.  试确定m,n的值，使下列关于x与y的多项式是一个五次三项式：

x^n-1y+(3-n)xy^n-2-nx^n-3y+4x^n-4y³-(m-2)x²y^n-4+(n-3)

答案：

一.ABBAC　　  DADDA

二.11.x-6　 12.关于x轴对称  13. 2　14.2ⁿ²,m　　  15.(x-a)(a-1)　　

16. 0　　 17.6xyz　　18. -3995　　19.k=2,b=3　　 20.

三. 21.32　22. -18y²+39xy　 23.-　24.11

25(0,1)　b=1,k=-2　27.1,　28. m=-3,n=5