2003年辽宁省六三制初二数学竞赛试题

考试时间：120分钟　　满分：120分

　　一、选择题(每小题3分，共30分)下面各题中只有一个答案是正确的，请将正确答案前的字母填在相应的括号内。

　　1、下列说法中，正确的是(　　)

　　A、是分式　　　　　　　　　　　B、正方形的对称轴有2条

　　C、等腰三有形是锐角三角形　　　　　D、等腰三角形是轴对称图形

　　2、下列各式是最简分式的是(　　)

　　A、　　　　　B、　　　　　C、　　　　　D、

　　3、一件工作，甲独做x天完成，乙独做y天完成，则甲、乙合作一天完成整个工作量的(　　)

　　A、　　　　　B、　　　　　　 C、　　　　 D、

　　4、在Rt△ABC中，若三边长分别是a、b、c，则下列不可能成立的结论是(　　)

　　A、a=3，b=4，c=5　　　　　　　　　　B、∠A：∠B：∠C=1：1：2

　　C、a：b：c=1：1：2　　　　　　　　　D、∠A+∠B=∠C

　　5、已知水厂A和工厂B、C正好构成一等边△ABC，现由水厂A为B、C两厂提供工业用水，要在A、B、C间铺设输水管道，有如下四种设计方案(图中实线为铺设管道路线)，其中铺设路线最短的方案是(　　)

　　

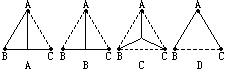
　　6、设a是小于1的正数，且b=，那么a，b大小关系为(　　)

　　A、a＞b　　　　　 B、a＜b　　　　　 C、a=b　　　　　D、不能确定

　　7、式子(m-2n-3)(m-2n+3)+9的算术平方根是(　　)

　　A、m-2n　　　　　　　　　　　　　

　　B、2n-m

　　C、当m≥2n时，m-2n；当m＜2n时，2n-m

　　D、当m≥2n时，2n-m；当m＜2n时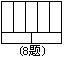，m-2n

　　8、如图，周长为68的矩形ABCD被分成7个全等的矩形，则矩形ABCD的面积为(　　)

　　A、98　　　　　　　B、196　　　　　 C、280　　　　　D、284

　　9、若0＜x＜1，则-等于(　　)

　　A、　　　　　　　B、-　　　　　　C、-2x　　　　　D、2x

　　10、若对应，则对应(　　)

　　A、　　　　　　B、　　　　　C、 　　　　D、

　　二、填空题(其中11题，12题各3分；其它题每题4分，满分30分)

　　11、已知=1，则的值等于____。

　　12、如果方程有增根，则a的值为____。

　　13、若a、b分别是8-的整数部分和小数部分，则2ab-b²=____。

　　14、九条平行于三角形一边的直线，把其他两边分别等分，分三角形为10个面积不等的部分，若其中最大部分的面积为19，那么原三角形的面积为____。

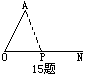
　　15、如图，OA=10，P是射线ON上的一动点，且∠AON=60°，则

　　(1)当OP=____时，△AOP为等边三角形。

　　(2)当OP=____时，△AOP为直角三角形。

　　　　　　

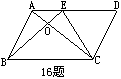
　　16、如图，E为平行四边形ABCD边上的一点，且AE=AD，AC与BE交于点O，若△AOE的面积为5cm²，则梯形ABCE的面积是____。

　　17、多项式x²+y²-6x+8y+7的最小值为____。

　　18、边长分别是3，5，8的三个正方体被粘合在一起，在这些用各种方式粘合在一起的立体中，表面积最小的那个立体的表面积是____。

　　三、解答题(19题、20题各6分，21题、22题各7分，满分26分)

　　19、已知+(xy-2)²=0，

　　求的值。

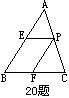
　　20、如图，在△ABC中，点P自点A向点C运动，过P作PE∥CB交AB于点E，作PF∥AB交BC于点F。问是否存在点P，使平行四边形PEBF是菱形？若存在，用尺规作图找到该点，并说明理由；否则也说明原因。

　　

　　21、(满分7分)观察下面式子，根据你得到的规律回答：

=____；=____；=____；

……　　……

求的值(要有过程)。

　　22、(满分7分)对于实数x，y，我们规定其运算x※y=ax^y+b+2。若1※2=870，2※3=884，求：3b+5a-600的值。

　　四、(23题、24题各8分，满分16分)

　　23、甲、乙两列火车各长180米，如果两列车相对行驶，从车头相遇到车尾离开共需12秒；如果两列车同向行驶，那么从甲的车头遇到乙的车尾直到甲的车尾超过乙的车头共需60秒。若两车速度不变，求甲、乙两车的速度。

　　24、(满分8分)如下图，八个正数排成一排，从第三个数开始，每个数都等于它前面两个数的乘积。现在用六个纸片盖住了其中的六个数，只露出第五个数是，第八个数是，请说出第一个数是什么？

　　□，□，□，□，，□，□，

　　五、(25题10分，26题8分，满分18分)

　　25、如图，在矩形ABCD中，AB=2，AD=4，DE=2CE，F为BC上一点，过F作GF∥AE，交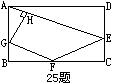AB于G，过G作GH⊥AE于H，若设BF=x，四边形GHEF的面积为S。

　　(1)求S_△BGF(用x表示)；

　　(2)求S关于x的关系式。

　　26、如图是由边长为1的五个小正方形拼在一起所组成的图形，如果任意剪裁后(不一定沿小正方形边线剪)，再拼在一起。

　　(1)能拼成一个矩形吗？如果能，请画出草图；

　　(2)能拼成一个等腰三角形吗？如果能，请画出草图；

　　(3)能拼成一个正方形吗？如果能，请画出草图。

2003年辽宁省六三制初二数学竞赛试题

参考答案及评分标准

一、选择题(每小题3分，共30分)

1、D　2、A　3、D　4、C　5、C　6、B　7、C　8、C　9、D　10、B

二、填空题(其中11题、12题各3分，其它题每题4分，共30分)

11、0　　12、1　　13、5　　14、100　　15、(1)10　(2)5　　16、80　　17、-18　　18、74

三、解答题

　　19、(满分6分)

解：由+(xy-2)²=0得x=1，y=2　　……1分

　　

　　

　　

　　……

　　　　……5分

　　将这些等式两边分别相加，即得原式=1-=　　……6分

　　20、(满分6分)

　　解：存在点P，使平行四边形PEBF是菱形。作∠B的平分线交AC于P，过P作BC的平行线PE交AB于E，过P作AB的平行线PE交BC于F(保留作图痕迹即可)　　……3分

　　理由如下：

　　∵EBFP为平行四边形，∴∠EPB=∠PBF

　　又∵∠EBP=∠PBF∴∠EBP=∠EPB

　　∴BE=EP

故平行四边形PEBF是菱形　　……6分

　　21、(满分7分)

解：=3

　　=33

　　=333　　……3分

　　……　……

　　则， 　　……4分

　　过程如下：

　　

　　=

　　=　　……7分

　　22、(满分7分)

解：　　……2分

　　即

　　②-①得a=2，b=866　　……5分

　　所以3b+5a-600=3×866+10-600=2008　　……7分

　　23、(满分8分)

解：设四列车的速度为x米/秒，乙列车的速度为y米/秒，依题意有

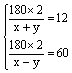　　　　……4分

　　解得x=18，y=12　　……7分

　　答：甲车的速度是18米/秒，乙车的速度是12米/秒　　……8分

　　24、(满分8分)

解：不妨设前四个数为a，b，c，d，第六个数、第七个数为e，f，则由已知，得

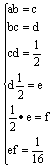　　　　……4分

　　由后边的两等式得f=，e=　　……6分

　　倒推可得a=　　……8分

　　25、(满足10分)

　　(1)∵GF∥AE ,∴∠BGF=∠BAE，又∠BAE=∠AED

　　且∠B=∠D=90°

　　∴△BFG∽△DAE，进而

　　，∴GB=BF=　　……2分

　　故S_△BFG=　　……3分

　　(2)又△AHG∽△FBG，设AH=a，GH=3a，则由勾股定理知

　　9a²+a²=(2-)²，即a²=(2-)²

　　则S_△AGH=a²=(2-)²　　……5分

　　而S_△FCE=·(4-x)·=(4-x)　　……7分

　　又S_△ADE=×4×=

　　S=8--(2-)²--(4-x)=-x²+x+　　……10分

　　26、(满分8分)

解：(1)能或或其它略　　……2分

　　(2)能或或其它略　　……4分

　　(3)能或或其它略　　……8分

注意：只要画出一种即给分，其它画只要正确参照给分。