城北中学八年级（上）第一学月测试题
(时间 90 分钟, 满分100分) 学号 姓名________________
（新的学年开始了，愿同学们好好把握时间┈蓬安•唐鹏寄语）
一. 填空（每题3分共30分）
1、在多边形内角和公式:N＝180ºn－360º中,变量是_________,常量是_________,自变量是_________,_________是_________的函数；
2、用10米长的绳子围成长方形,它的面积S(米)与长x(米)的函数的表达式是_______ __；
3、已知一次函数y＝kx＋5的图象经过点（－1，2），则k= ；
4、一次函数y＝－2x＋4的图象与x轴交点是 ，与y轴交点是 __ _；
5 、
函数
中自变量x的取值范围是 ___ ___；
6、某种储蓄的月利率为0.15%，现存入1000元，则本息和y（元）（不计利息税）与所存月数x之间的函数关系式是 ；
7、写出图象经过点（1，-3）的一次函数表达式（写出一个即可） ；
8、某商店出售一种瓜子，其售价y（元）与瓜子质量x（千克）之间的关系如下表
| 质量x（千克） | 1 | 2 | 3 | 4 | … |
| 售价y（元） | 3.60+0.20 | 7.20+0.20 | 10.80+0.20 | 14.40+0.20 | … |
由上表得y与x之间的关系式是 ；
9、某人用充值50元的IC卡从A地向B地打长途电话，按通话时间收费，3分钟内收费2.4元，以后每超过1分钟加收1元，若此人第一次通话t分钟（3≤t≤45），则IC卡上所余的费用y（元）与t（分）之间的关系式是 ；
10、x 时，函数
满足y＜0；x 时，函数
与
的值相等，这个函数值是
。
二．选择题（每题2.5分，共25分）
11、下列函数（1）y=πx (2)y=2x-1 (3)y＝ (4)y＝
－3x (5)y＝
2－1中，是一次函数有（ ）（A）4个（B）3个（C）2个（D）1个
12、已知点（-4，y1），（2，y2）都在直线y＝－ x＋2上，则y1 与y2大小关系是( )（A）y1 >y2 （B）y1 =y2 （C）y1 <y2 （D）不能比较
13、一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的高度h(厘米)与燃烧时间t(时)的函数关系的图象是( )
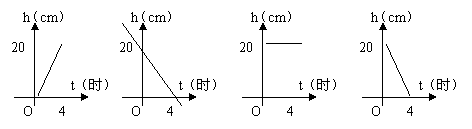
(A) (B) （C） （D）
14、在函数
的图象上的点是（
）
A.(－2, －2) B. (－2, －4) C. (－2, －5) D. (－2, －3)
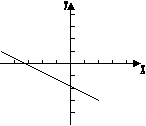15、已知一次函数y＝kx＋b的图象如图所示,则k、b
的符号是( )
(A)k＞0,b＞0 (B)k＞0,b＜0
(C)k＜0,b＞0 (D)k＜0,b＜0
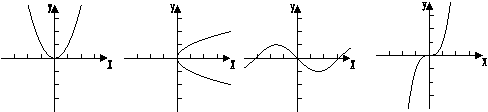16、下列各曲线中不能表示y是x的函数是（
）
A B C D
17、已知：正方形的周长为x，它的边长为y，则y与x的函数关系是（ ）A.y＝4x B.y＝
C.y＝2x D.y＝
18、如图，直线
与x轴的交点为(－3,0)则y＞0时x的取值范
围是（ ）
A.x＞－3 B.x ＞0 C.x＜－3 D. x＜0
19、把直线
向下平移2个单位长度所
得直线的解析式为（ ）A.
+5
B. +2 C.
+1
D. －2
20、如图，直线y1 = k1x与y2=k2x＋b交于A，则x取（ ）时，y1 ＜y2 A.x＞4 B.x ＞0 C.x＜4 D. x＜0
二、 解答题(第21~24题每题6分,第25~27题每题7分,共45分)
21、在同一坐标系中,作出函数y＝－3x与y＝ x＋1的图象. (只作图)
y1
y2
(20小题)
A（4，4）
22、已知点A（－1，a）与B（2，b）都在直线
上，试用两种以上的方法比较a与b的大小；
23、已知y－2与x成正比,且当x＝－2时,y＝4
(1)求y与x之间的函数关系式 (2)求当y＝－4时，x的值；
24、已知直线y＝kx＋b经过点(－1, －5),且与正比例函数y＝ x的图象相交于点(2,a),求：(1)a的值 (2)k,b的值
 |
11
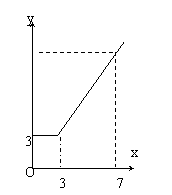
25、如图是某出租车单程收费y(元)与行驶路程x
(千米)之间的函数关系图象,根据图象回答下列问题
(1)当行使7千米时,收费应为 元；
(2)求收费y(元)与行使x(千米)之间的函数关系式？
26、为了加强公民的节水意识,某市规定如下用水收费标准:每户每月的用水量不超过6立方米时,水费按每立方米a元收费；超过6立方米时,超过的部分每立方米按c元收费,该市某户今年9、10月份的用水量和所交水费如下表所示，设某户每月用水量x(立方米),应交水费y(元)。
| 月份 | 用水量(m3) | 收费(元) |
| 9 | 5 | 7.5 |
| 10 | 9 | 18 |
（1）求a,c的值
（2）当x≤6,x≥6时,分别写出y与x的函数关系式
（3）若该户11月份用水量为8立方米,求该户11月份水费是多少元?
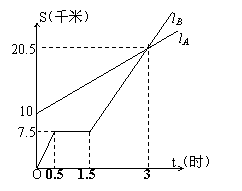27、如图，lA、 lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系。
（1）B出发时与A相距 千米。
（2）走了一段路后，自行车发生故障，进行
修理，所用的时间是 小时。
（3）B出发后 小时与A相遇。
（4）求出A行走的路程S与时间t的函数关系式。