2003—2004学年度第一学期期末初二数学试题
考试时间(90分钟)满分120分
一、 填空题(每空2分,共30分)
 1.
1. ![]() ,
,![]() 的算术平方根的平方根是 。
的算术平方根的平方根是 。
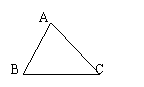
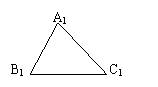
2. △![]() 是△
是△![]() 平移后得到的三角形,则
平移后得到的三角形,则
|
3. 菱形有一个内角是![]() ,边长为10,则它的面积是 。
,边长为10,则它的面积是 。
4. 正方形的对角线 、 、 ,且每一条对角线平分一组对角。
 5. 三角形的三条中线交于一点,这个点是三角形的 。
5. 三角形的三条中线交于一点,这个点是三角形的 。
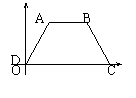
6. 如图,等腰梯形ABCD中,![]() ,AB=4,CD=10,则各顶
,AB=4,CD=10,则各顶
点的坐标是A(7,0) B ,C , D(0,0)。
7. y吨货物用x辆卡车去装,每车装7吨,还有3吨没装上,可列
出方程 ,其中y是否可以看作x的函数(填是或否) 。
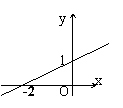 8. 如图所示,图中函数的解析示为
。
8. 如图所示,图中函数的解析示为
。
9. 一次函数y=-2x+b与x轴交于(4,0),则它与y轴的交
点为 ,与直线y=x的交点坐标为 。
二、选择题(每小题3分,共18分)
1. 下列说法正确的有 个。
① 任何正数的两个平方根的和等于0 ② 任何实数都有一个立方根
③ 无限小数都是无理数 ④ 实数和数轴上的点一一对应
A. 1 B. 2 C. 3 D. 4
2. 矩形ABCD的对角线AC,BD所成的锐角是60度,则 。
A. AC+BD=AB+BC+CD+DA B. BD+AC=AB+AC C.BD=2AB D.以上都不对
3. 一个多边形的每个内角都等于![]() ,则内角和是 ,共有
条对角线。
,则内角和是 ,共有
条对角线。
A. ![]() , 8
B.
, 8
B. ![]() , 10 C.
, 10 C. ![]() , 9
D.
, 9
D. ![]() , 11
, 11
4. 下列表述的图形中能进行密铺的有 种。
① 平行四边形 ② 三角形 ③直角梯形 ④正五边形 ⑤正八边形
A. 1 B. 2 C. 3 D. 4
5. 方程2x+y=7在自然数范围内的解有 对。
A. 4 B. 3 C. 2 D. 1
6. 点P(![]() )关于x轴对称与关于y轴对称的点的坐标相同,则
)关于x轴对称与关于y轴对称的点的坐标相同,则![]() 的值分别是 。
的值分别是 。
A. –1, 2 B. –1, –2 C . –2, 1 D. 1, 2
三、 解答题:
3、作图题:(6分)将△![]() 平移后,A点移到A1点,请作出平移后的图形,并将此图形绕点C1逆时针旋转
平移后,A点移到A1点,请作出平移后的图形,并将此图形绕点C1逆时针旋转![]() ,再作出所得图形。
,再作出所得图形。
 |
| |||
1.化简二次根式:(每小题3分,共9分)
(1)![]() (2)
(2)![]() (3)
(3)![]()
 |
4、(8分)如图,菱形ABCD中,E是AD中点,
EF⊥AC交CB的延长线与点F。
(1) DE和BF相等吗?请说明理由。
(2) 连结AF、BE,四边形AFBE是平
行四边形吗?说明理由。
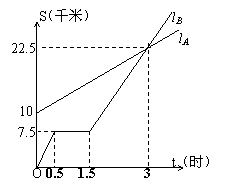 5、(16分)如图,lA lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系。
5、(16分)如图,lA lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系。
(1)B出发时与A相距 千米。(2分)
(2)走了一段路后,自行车发生故障,进行
修理,所用的时间是 小时。(2分)
(3)B出发后 小时与A相遇。(2分)
(4)若B的自行车不发生故障,保持出发时
的速度前进, 小时与A相遇,相遇点
离B的出发点 千米。在图中表示出
这个相遇点C。(6分)
(5)求出A行走的路程S与时间t的函数关系式。(写出过程,4分)
6、(9分)在一次射击比赛中,19名参赛队员(每人打3发)的成绩如下表:
| 成绩(环) | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 人数 | 1 | 1 | 2 | 2 | 4 | 7 | 2 |
(1) 求出这组数据的平均数,众数,中位数。
(2) 在此问题中,平均数,众数,中位数各说明了什么
7、列方程组解应用题:(8分)
甲、乙两种商品原来的单价和为100元,因市场变化,甲商品提价40%,乙商品降价10%,两种商品的单价和比原来提高了20%,甲、乙两种商品原来的单价各是多少元?
8、请你用树状图的方式排列一下本学期数学课本中的主要内容。(5分)写在背面
9、设计题(3分)
![]() 如图,等腰梯形的一条对角线将它分成了两个三角形,用这两个三角形能否进行密铺,如果能,请设计一个密铺图案,如果不能,请说明理由。
如图,等腰梯形的一条对角线将它分成了两个三角形,用这两个三角形能否进行密铺,如果能,请设计一个密铺图案,如果不能,请说明理由。
