/***　　　　　　　　　  学校　　　　　　  　　　姓名　　　　　  　　　 班级　　　　　　　　 学号　　　　  　　　　　　　*** ***　　　 　　　　　 密　　　　 封　　　　  线　　　　  内　　　　  不　　　　  得　　　　  答　　　　  题　　　　　 ***

2003-2004学年度八年级上学期期末考试

数 学 试 题

（本试题满分：100分　时间：120分钟 命题人：阳溪中学杨川）

题  号	一	二	三	四	五	总  分
得  分

致考生：

　　本试卷分A卷和B卷，其中A卷80分为必答题，题目源自课本，是学习数学的基本要求，在做的过程中回想一下所学知识、仔细作答，你定会有满意的成绩；B卷20分，可根据要求选择自己喜欢的题目作答，相信你会有新的创意和聪明的想法！祝考试顺利、成功！

A卷（80分）

一、　　　　　 填空题：(每空1分，共28分)

1、平移后的图形与原来的图形的对应线段　　　　 ，对应角相等，图形的形状与大小　　　　 .

2、如图1，∠DEF是∠ABC经过平移得到的，若∠ABC＝31°，则∠DEF＝　　　　

3、图形旋转是由　　　　和　　　　所决定的。

图1

4、如图2，△ABC是等腰三角形，D点是BC上一点，△ABD经过旋转后到达△ACE的位置，则旋转中心是　　　，旋转了　　　度。

5、如图3，电扇的图片是一个旋转对称图形，电扇的叶片旋转_______度能与自身重合

6、已知在　 ABCD中，∠A＝60°，AB＝5，BC＝3，则∠C＝　　　，它的周长等于　　　　

7、已知菱形的两条对角线的长分别为6cm和8cm，则菱形的面积等于　　　　。

8、不等式－2x＜4的解集是　　　　　。

9、用不等号填空：若a<b，则a－1_____b－1，-3a____-3b

10、不等式组的解集为_________.

11、用不等式表示：

①　  y的2倍小于3　　　　　　　

②　  a是非负数　　　　　

③　  y的与3的差是负数　　　　　　

12、化简a² (－a)³＝________.

13、计算：①=　　　　　　②(a²)⁴=　　　　③（－xy²）³＝　　　　

14、分解因式：①a²－1＝__________.②x²－x＋＝　　　　　　，③3a²b-6ab³＝　　　　　

15、抛掷一枚质地均匀的正八面体骰子一次，如果每面分别写着数字１～８，那么可能观察到的结果共有________个，它们是_________________

16、必然事件的机会是　　　　。

二、　　　　　 选择题（每题2分，共16分）。每题只有一个答案是正确的，请将正确的答案填在括号内。

17、下列运算中，正确的是（　　　）

A、7⁴×7⁴＝7¹⁶　　B、(a⁴)⁴＝a⁴a⁴　　C、（－x）²＝－x²　　D、（－x）³＝－x³

18、下列图形中既是中心对称图形又是轴对称图形的是

　

　　　（A）　　　　　　　（B）　　　　 （C）　　　　　　 （D）

19、下列等式中，正确的是

A、（－a－b）²＝（a＋b）²　　　　B、；

C、[（－2）a³]²＝－4a⁶；　　　　D、（－a²b³c）²＝a⁴b⁶c

20、如果a是任意有理数，那么下列不等式中，一定成立的是（　　）

A、a＞0　　　　B、2a＞a　　　　C、a²＋1＞0　　　　D、a²＞0

21、正方形具有而菱形不一定具有的特征是（　　）

　　A、对角线互相平分　　  B、对角线互相垂直

C、对角线相等　　　　  D、对边平行且相等

22、下列条件中能判定四边形ABCD是平行四边形的是

　　A、AB＝AD，CB＝CD　　 　　 B、AB∥CD，AD＝BC

C、AB＝CD，AD＝BC　　　　  D、∠A＝∠B，∠C＝∠D

22、下列几何图形：①平行四边形　②线段　　 ③等边三角形　④矩形　　 ⑤等腰梯形，其中为中心对称图形的个数为

　A、2个　B、3个 C、4个 D、5个

23、如图,在□ABCD中，对角线AC、BD交于点O，过点O的直线分别交BC、AD于F、E．若AD＝6cm，AB＝5cm，OE＝2cm，则梯形EFCD的周长是

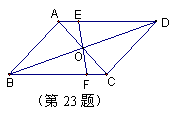　　A、16cm　　 　 B、15cm 　　 C、14cm　　D、12cm

三、　　　　　 解答题：

24、计算：（3分）

　（1）（－2a）³（2a－5ab）　

25、因式分解：（每小题3分，共6分）

　（1）a³－2a²＋a　　　　　　　（2）25x²－（2x－y）²

26、解不等式（组）（第1小题3分，第2小题4分，共7分）

（1）　　　　　

（2）、，并把它的解集在数轴上表示出来

27、（3分.）如图，△ABC中M为BC的

中点，求作△ABC关于M成中心对称的图

形

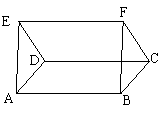
28、(4分)如图，已知平行四边行ABCD和平行四边形DCFE，试说明AE∥BF

			A

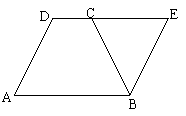
29、（5分）如图，在等腰梯形ABCD中，AB∥DC，E是DC延长线上的一点，BE=BC，试说明∠A和∠E的关系。

29、（4分）有人说：“班级里分到一张参加现场演唱会的门票，为公平起见，班长让每个人来抽签，这样每个人都有50%的机会。”，谈谈你的看法。

30、 (5分)在世纪公园的售票口贴有如下的海报：

	个人票价：5元/人 团体票价：4元/人（不少于30人）

（1）　  如果八年级（5）班的27名同学去世纪公园开展活动，那么他们至少要花多少钱用于买门票；(2分)

（2）　  你能针对该班参加活动各种可能的人数，设计合理的购票方案吗？(3分)

B卷（20分）

四、填空题：（选做5处，每空2分，共10分）

1、菱形的一个内角是120°，且平分这个内角的对角线长为8cm，则这个菱形的周长是_________.

2、如图（1）已知矩形宽为a，用a表示阴影部分面积　　　　　　　　　  ；如图（2）已知大圆半径为r，用r表示阴影部分面积　　　　　　　　  ；

3、某种出租车的收费标准是：起步价5元(即行驶距离不超过3千米都需付5元车费)， 超过3千米以后，每增加1千米，加收1.4元(不足1千米按1千米计)．某人乘这种出租车从甲地到乙地共支付车费12元，设此人从甲地到乙地经过的路程是x千米，那么x的最大值是　　　　　

4、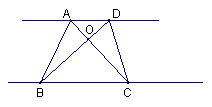若不等式(m+7)x>6的解集是x<，则m的范围为　　　　

5、如右图，AD∥CD，AC、BD相交于点O，则面积相等的三角形有　　　　 对.

6、若，则x的取值范围为　　　　　 .

7、小明生日宴会上，要把一个大蛋糕分成七块，问他最少要切　　  次（切割成的蛋糕面积不一定相等）

五、解题答：（以下1、2选做一题6分，3、4选做一题4分）

1、平行四边形ABCD中，对角线AC、BD相交于点O，若E、F是AC两动点，分别从A、C两点以相同的速度1cm/s向C、A运动，

（1）四边形DEBF是平行四边形吗？说明你的理由；

（2）若BD＝10cm，AC＝16cm，当运动时间t为何值时，

四边形DEBF是矩形.

2、如图，在矩形ABCD中，对角线AC与BD相交于点O，

（1）画出△AOB平移后的三角形，其平移方向为射线AD的方向，平移的距离为线段AD的长.

（2）设（1）中O点平移后的对应点为E，试判断四边形CODE的形状.并说明你的理由.

（3）当四边形ABCD是什么四边形时，（2）中的四边形CODE是正方形.

3、计算：（2＋1）（2²＋1）（2⁴＋1）（2⁸＋1）＋1

4、K为何值时，x²＋kx＋1恰好是另一个整式的平方？

命题说明：

本试卷参照《国家基础教育课程改革实验区开展中小学期末评价与考试改革的建议》的要求，考试的内容要以课程标准为依据，体现新的人才观和教育观，关注学生的探究、实践和创新能力，考试中要加强与社会实际和学生生活实际相联系的内容。命题与学生的生活实际联系的同时，还参照学生学习的实际情况、考察学生数学基本知识和基本技能，不出人为编造的偏题和怪题，重在学生的思考方法的考察，面向大多数同学命题，同时兼顾学有余力的同学能够充分发展自己的特长，允许学生根据自己的实际情况选择考试题目。

A卷80分，题目多数源自书本上的例题、练习题、作业等。题目简单，一看就懂，主要考察学生书本知识的和基本技能的掌握情况，计算量小，学生容易得分，也比较容易提起学生在考试过程中的兴趣，使他们容易得分，从而减轻考试的心理负担。

B卷20分，题目探索性强，掌握学生学习知识的运用情况，考察学生的特长，认真思考后，还是比较容易答题，如有做不了的，还允许学生可以选择自己熟悉或容易的题目来做，个别不会做的，也不影响学生本堂考试的分数，不会因为一题不会，造成学生在考试中的思想负担，从而愉快答题。