2003—2004学年度八年级第二学期期中考试

数学试卷

时间：100分钟　 满分：100分

评分：___________

一、填空题：（每小题2分，共20分）

1、用不等式表示“x的5倍是非负数”得___________。

2、分解因式：______________________。

3、分解因式：______________________。

4、分式中，当x______时，没意义；当x______时，值为零。

5、约分：___________。

6、若是一个完全平方式，则k=___________。

7、关于x的方程有增根，则增根为_______，m的值为___________。

8、当分式的值为负时，x的取值范围是________________。

9、登山前，登山者要将矿泉水分装在旅行包内带上山。若每人2瓶，则剩余3瓶，若每人带3瓶，则有一人所带矿泉水不足2瓶。登山有___________人。

10、若则___________。

二、选择题：（每小题3分，共30分）

题号	1	2	3	4	5	6	7	8	9	10
答案

1、下列代数式是分式的是：（　）

　　 A、　　　　 B、　　　　　　 C、　　　　  D、

2、已知两个不等式的解集在数轴上如图表示，那么这个解集为（　 ）

　A、≥－1　 B、>1　 C、－3<≤－1　　　D、>－3

3、下列四个从左到右的变形中，是因式分解是的（  ）

　　 A、　　　　　 B、

C、　　  D、

4、若分解因式，则a与b的值为（　 ）

　　 A、a=2，b=7　　 B、a=2，b=－7　　C 、a=－2，b=7　  D、 a=－2，b=－7

5、下列各式中最简分式是（　 ）

　　 A、　　　 B、　　　 C、　　　 D、

6、当x为任意有理数时，下列分式中一定有意义的是（　 ）

　　 A、　　　　B、　　　 C、　　　 D、

7、能被60和70之间的某两位数整除，则这两个数是（　　）

　　 A、62，64　　　　B、66，68　　　 C、63，65　　　　  D、67，69

8、如图所示：OA、OB分别表示甲乙两名学生运动的一次函数，图中S和t分别表示运动路程和时间，根据图表判断快者的速度比慢者的速度每秒钟快（　 ）

　　 A、2.5米　　　　 B、2米　　　　  C、1.5米　　　　D、1米

9、已知中，y是正数，则m的取值范围是（　 ）

　　 A、m<2　　　　　　　 B、m<3　　　　 C、m<4　　　D、m<5

10、一项工程，A单独做m小时完成，A、B合做20小时完成，则B单独做需（  ）小时完成。

　　 A、　　　　 B、　　　　　 C、　　　　  D、

三、解答题：（共8题，合计50分）

1、（5分）解不等式组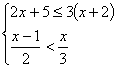

2、（5分）求不等式的非负整数解。

3、分解因式：（每小题4分，共8分）

①　　　　　　　　　　　　　　  ②

4、解下列分式方程：（每小题5分，共10分）

①　　　　　　　　　　　　　 ②

5、（6分）先化简，后求值：

1

6、（6分）我市移动通讯公司开设了两种通讯业务，A类是固定用户：先缴50元基础费，然后每通话1分钟再付话费0.4元；B类是“神州行”用户：使用者不缴月租费，每通话1分钟通话费0.6元（这里均指市内通话）。若果一个月内通话时间为分钟，分别设A类和B类两种通讯方式的费用为，

　　　　（1）写出、与之间的函数关系式。

　　　　（2）一个月内通话多少分钟，用户选择A类合算？B类呢？

（3）若某人预计使用话费150元，他应选择哪种方式合算？

7、（列分式方程解应用题，5分）某医用制剂厂原计划生产某种消毒液960吨，由于抗击“非典”的紧急需要，在保证质量的前提下，开工后工人们每天的生产量是原计划的2倍，结果提前4天完成任务，原计划每天生产多少吨？

8、（5分）某厂有甲、乙两种原料配制成某种饮料，已知这两种原料的维生素C含量及购买这两种原料的价格如下表：

原料 维生素C及价格	甲种原料	乙种原料
维生素C/（单位/千克）	700	200
原料价格/（元/千克）	10	6

现配制这种饮料20千克，要求至少含有5000单位的维生素C，并要求购买甲、乙两种原料的费用不超过136元，

（1）设需用千克乙种原料，写出应满足的不等式组。

（2）按上述的条件购买乙种原料应在什么范围之内？