第二章实数复习小结
一、 知识结构
 |
二、 基础知识回顾
1．无理数的定义
（ ）叫做无理数
2．有理数与无理数的区
有理数总可以用（ ）或（ ）表示；反过来，任何（ ）或（ ）也都是有理数。而无理数是（ ）小数，有理数和无理数区别之根本是有限及无限循环和无限不循环。有理数可以化成（ ），无理数不能化成（ ）。
3.常见的无理数类型
(1) 一般的无限不循环小数，如：1.¨···
(2) 看似循环而实际不循环的小数，如0.···(相邻两个1之间0的个数逐次加1)。
(3) 有特定意义的数，如：π=3.···
(4).开方开不尽的数。如：
。
4．算术平方根。
（1） 定义：
（2） 我们规定：
（3）
性质：算术平方根
具有双重非负性：
① 被开方数a是非负数，即a≥0.
②
算术平方根本身是非负数，即≥0。
也就是说，（ ）的算术平方根是一个正数，
0的算术平方根是（ ），
（ ）没有算术平方根。
5．平方根
（1） 定义：
（2） 非负数a的平方根的表示方法:
（3） 性质： 一个（ ）有两个平方根，这两个平方根( )。
( )只有一个平方根，它是( )。
( )没有平方根。
说明：平方根有三种表示形式：± ， ，－，它们的意义分别是
：非负数a的平方根，非负数a的算术平方根，非负数a的负平方根。要特别注意： ≠±。
6.平方根与算术平方根的区别与联系：
区别：①定义不同 ②个数不同：
③ 表示方法不同：
联系：①具有包含关系：
②存在条件相同：
③ 0的平方根和算术平方根都是0。
7．开方运算：
（1） 定义：
① 开平方运算：
② 开立方运算：
（2）平方与开平方式（ ）关系，故在运算结果中可以相互检验。
8．a2的算术平方根的性质
①当a≥0时，
=（ ） ② 当a<0时，=（ ）
一般的，当a<0时，=-a.
我们还知道，当a≥0时，│a│=a；当a<0时，│a│=a.
综上所述，有
a (a≥0)
=│a│=
-a (a<0)
从算术平方根的定义可得：
=a (a≥0)
9．立方根
（1） 定义：______________________________.
（2） 数a的立方根的表示方法:_________
（3） 互为相反数的两个数的立方根之间的关：_________
（4）
两个重要的公式
10．实数
（1） 概念：________和________统称为实数。
（2） 
分类 按定义
_______
________
_______
________ ___ 有限小数或________小数
_______
实数 ________
_______
_________
________ 无限不循环小数
_________
按大小 正实数
实数 零
负实数
(4) (3)实数的有关性质
(5) ⑴a与b互为相反数〈=〉a+b=0
(6) ⑵a与b互为倒数〈=〉ab=1
(7) ⑶任何实数的绝对值都是非负数，即
≥0
(8) ⑷互为相反数的两个数的绝对值相等, 即=
⑸正数的倒数是正数;负数的倒数是负数;零没有倒数.
（4）实数和数轴上的点的对应关系：
实数和数轴上的点是一一对应的关系
（5） 实数的大小比较
1． 在数轴上表示的两个数，右边的数总比左边的数大。
2． 正数大于零，零大于负数，正数大于一切负数，两个负数比较，绝对值大的反而小。
（6） 实数中的非负数及其性质
在实数范围内，正数和零统称为非负数
我们已经学过的非负数有如下三种形式
(9) ⑴任何一个实数a的绝对值是非负数，即≥0
(10) ⑵任何一个实数的平方是非负数，即
≥0；
(11) ⑶任何一个非负数a的算术平方根是非负数，即≥0
(12) 非负数有以下性质
(13) ⑴非负数有最小值零
(14) ⑵有限个非负数之和仍然是非负数
(15) ⑶几个非负数之和等于0，则每个非负数都等于0。
(16) 11..二次根式的两条运算法则
(17) 
（
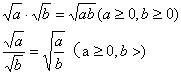
实数练习题二
一、判断题
（1）带根号的数一定是无理数（ ）； （2）无理数都是无限小数（ ）；
（3）无理数包含正无理数、0、负无理数（ ）；（4）4的平方根是2（ ）；
（5）无理数一定不能化成分数（ ）； （6）
是5的平方根（ ）；
（7）一个正数一定有两个平方根（ ）； （8）
25的平方根是
（ ）
（9）互为相反数的两数的立方根也互为相反数（ ）；
（10）负数的平方根、立方根都是负数（ ）；
（11）①无理数是无限小数（ ）；②无限小数是无理数（ ）；③开方开不尽的数是无理数（ ）；④两个无理数的和是无理数（ ）；⑤无理数的平方一定是有理数（ ）；
二、填空题
（12）把下列各数填入相应的集合中（只填序号）：
①
②
③
④
⑤0 ⑥
⑦
⑧
有理数集合：｛ …｝无理数集合：｛ …｝正实数集合：｛ …｝负实数集合：｛ …｝
（13）把下列各数填入相应的集合中（只填序号）：
①3.14 ②
③
④
⑤0 ⑥
⑦ ⑧0.15
有理数集合：｛ …｝正数集合｛ …｝
无理数集合：｛ …｝负数集合｛ …｝
（14）36的算术平方根是 ，1.44的平方根是 ，11的平方根是 ，
的平方根是
，
的算术平方根是 ， 
是 的平方。
（15） 
的相反数是 、倒数是 、绝对值是
。
（16） 满足
的整数
是
.
（17） 一个正数的平方等于144, 则这个正数是 , 一个负数的立方等于27,
则这个负数是 , 一个数的平方等于5, 则这个数是 .
（18）. 若误差小于10, 则估算
的大小为
.
（19） 比较大小: 
4.9; 
.(填“>”或“<”)
(20). 化简: 
=
, 
=
, 
= .
(21) .9的算术平方根是 ___、3的平方根是 ___, 0的平方根是 ___,-2的平方根是 .
(22). –1的立方根是 ,
的立方根是 , 9的立方根是 .
(23) .
的相反数是 , 倒数是 ,
-
的绝对值是 .
(24). 比较大小: ; 
; 
2.35.(填“>”或“<”)
(25). 
. 
, 
= .
(26)．一个数的平方根与立方根相等，这个数是______;立方根等于本身的数是_________. 平方根等于本身的数是________；算术平方根等于本身的数是_____________.
大于0小于
的整数是_________；
＜x＜
的整数x是__________.
(27).
(35)
.
(36)使
（37）已知
三、 选择题：
1. 边长为1的正方形的对角线长是（ ）
A. 整数 B. 分数 C. 有理数 D. 不是有理数
2. 在下列各数中是无理数的有( )
-0.333…, 
, , 
, 3, 3.1415, 2.010101…(相邻两个1之间有1
个0),76.…(小数部分由相继的正整数组成).
A.3个 B.4个 C. 5个 D. 6个
3. 下列说法正确的是( )
A. 有理数只是有限小数 B. 无理数是无限小数
C. 无限小数是无理数
D. 
是分数
4. 下列说法错误的是( )
A. 1的平方根是1 B. –1的立方根是-1
C. 是2的平方根
D. –3是
的平方根
5. 若规定误差小于1, 那么
的估算值为( )
A. 3 B. 7 C. 8 D. 7或8
6. 下列平方根中, 已经简化的是( )
A. 
B.
C.
D. 
7． 
的平方根是( )
A. 9 B. ±9 C. 3 D. ±3
8． 下列说法正确的是( )
A. 无限小数都是无理数 B. 带根号的数都是无理数
C. 开方开不尽的数是无理数 D. 是无理数, 故无理数也可能是有限小数
9． 方根等于本身的数是( )
A. –1 B. 0 C. ±1 D. ±1或0
10． 
的值是( )
A. 3.14-
B.
3.14 C. –3.14 D. 无法确定
11． 
为大于1的正数, 则有( )
A. 
B. 
C.
D. 无法确定
12． 下面说法错误的是( )
A. 两个无理数的和还是无理数 B. 有限小数和无限小数统称为实数
C. 两个无理数的积还是无理数 D. 数轴上的点表示实数
13.下列说法中不正确的是（ ）
A.42的算术平方根是4 B.
C.
D. 
14. 121的平方根是±11的数学表达式是（ ）
A. 
B.
C. ± D.±
15.如果
则x=( )
A.16 B.
C.±16 D.±
16. 
的平方根是（ ）
A.±8 B.±2 C.2 D.±4
17.下列说法中正确的是（ ）
A.±
的立方根是2 B.
C.两个互为相反数的立方根互为相反数 D.(-1)2的立方根是-1
18、-
的平方根是（ ）A.±√2 B.-√2 C.±2 D.2
19、估计
（ ）
A.7～8之间 B. 8.0～8.5之间 C. 8.5～9.0之间 D.9.0～9.5之间
20、在实数范围内，下列说法中正确的是（ ）
四、 化简:
①
-
;
②
;
③
;
④
.
⑤
.
⑥
;
⑦
.
⑧
五、解答题
1.
在数轴上作出对应的点.
2．估算下列各式的值
3．解方程 （1） 
（2）
4．
的值.
5.．已知2a-1的平方根是±3， 3a+b-1的算术平方根是4，求a+2b的平方根
6.
自由下落的物体的高度
(米)与下落时间
(秒)的关系为=4.9
.有一学生不慎让一个玻璃杯从19.6米高的楼上自由下落, 刚好另有一学生站在与下落的玻璃杯同一直线的地面上, 在玻璃杯下落的同时楼上的学生惊叫一声. 问这时楼下的学生能躲开吗? (声音的速度为340米/秒)
7．小芳想在墙壁上钉一个三角架(如图), 其中两直角边长度之比为3:2,
斜边长
厘米, 求两直角边的长度.
8． 小东在学习了
后, 认为
也成立,因此他认为一个化简过程: 
=
是正确的. 你认为他的化简对吗?如果不对请写出正确解题过程。