初二数学能力测试题

（折纸问题）

一、填空题：

1、把边长为1的正方形对折n次后，所得图形的面积是　　　　。

2、将矩形ABCD纸对折，设折痕为MN，再把B点叠在折痕MN上（如图1上点B），若AB=，则折痕AE的长是　　　　，△AEF是　　　 三角形。

3、如图2，矩形纸片ABCD沿对角线BD折叠，设点D落在D¹处，BC¹交AD于E，=6cm，BC=8cm，则S_阴=　　　　　  。

4、如图3，折叠矩形纸片ABCD的一边AD，点D落在BC边的点F处，已知AB=8cm，BC=10cm,则EC=　　　 。

5、如图4，把矩形纸片折叠，使点落在AD边的中点C¹处，设折痕为EF，AB=3，BC=4，则CE：BE=　　　　　 ，CF：FD　　　　  。

6、如图5，把矩形ABCD纸片折叠，使点D与点B重合，则四边形BEDF是　 形；若AB=6，BC=8，则折痕EF=　　　　 。

7、如图6，AD是△ABC的中线，∠ADC=45°，把△ADC沿AD对折，点C落在C¹的位置，则BC¹与BC之间的数量关系是　　　　　  。

8、如图7、把一张长方形ABCD的纸片，沿着EF折叠后，ED和BC的交点为G，点D、C分别落在D¹、C¹的位置上，若∠EFG=55°，则∠1=　　　 度。

9、如图8，将△ABC折叠成图8，则折出两条定理，这两条定理是：

　 ①　　　　　　 ；②　　　　　　  。

10、如图9，在△ABC中，周长为22，AB=AC，BC=6，现把线段AB对折，设折痕为DE，则△BEC的周长是　　　　  。

11、如图10，折叠矩形ABCD，先折出折痕（对角线）BD，再折叠AD，使AD边落在折痕BD上，得折痕DG，若AB=2，BC=1，则AG=　　　　。

12、如图11，把边长为a的等边△ABC折叠，使点A落在BC边的点D，且BD：DC=2：3，设折痕为MN，则AM：AN的值是　　　　 。

13、如图12，一边长为250cm的正方形ABCD纸片，AD上有一点P，且AP=　，折这纸片使点B落在点P上，则折痕EF的长是　　　　cm。

14、如图13，EF为正方形纸ABCD的对折线，将∠A沿DK折叠，使它的的顶点A落在EF上的G点，则∠DKG的度数是　　　　。

15、如图14，沿正方形对角线对折，互相重合的两个小正方形内的数字的求积等于　　　　　  。

二、解答下列各题：

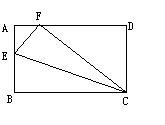
1、如图，ABCD是矩形纸片，E是AB上一点，且BE：EA=5：3，EC=15，把△BCE沿折痕EC向上翻折，若点B恰如落在AD的边上，设这个点的F，求AB、BC的长各是多少？

码　　　　　　　　　　　　　　　　　　　　　　　　

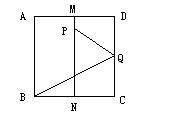
2、如图，有一块面积为1的正方形ABCD，M、N分别为AD、BC的中点，将C点折到MN上，落在点P的位置，折痕为BQ，连结PQ，（1）求MP；（2）求证：以PQ为边长的正方形的面积等于。

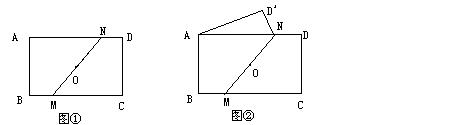
3、已知在矩形ABCD中，AD>AB，O为对角线的交点，过O作一直线分别交BC、AD于M、N。

（1）求证：梯形ABMN的面积等于梯形CDNM的面积（如图①）

（2）如图②，与MN满足什么条件时，将矩形ABCD以MN为折痕，翻折后能使C点恰好与A点重合？（只写出满足的条件，不要求证明）

（3）在（2）的条件下，若翻折后不重叠部分的面积是重叠部分的面积的，求BM：MC的值。