天津益中学校2001-2002学年度第二学期期中检测

八年级代数试卷

一、填空

1．若方程(m-3)x^m-1+3x-2=0是一元二次方程,则m=___________。

2．用配方法解一元二次方程2x²+3x+1=0，变形为（x+m）²=k,则m=_____,k=______。

3．在实数范围内分解因式：3x²+4xy-2y²=________。

4．若关于x的方程2x²+bx+c=0的两根分别是b,c那么bc=_______。

5．关于x的方程x²+kx+16=0有两个相等的正实数根，则k=_____。

7．关于x的方程x²-x+m=0两根差的平方小于1，则m的取值范围是_______。

8．x,y为实数，（x²+1+y²）(x²+y²)=12,那么x²+y²=___________。

9．若关于x的一元二次方程2x(kx-4)-3x²+6=0没有实数根，则k的最小整数值为_____。

10．已知方程x²+(m+1)x+m²+m=0有一根为0，则m=_______。

二、单选：

1．关于x的方程ax²+bx+c=0,已知a>0,b>0, c<0,则下列结论正确的是（ ）

（A）有两个正实数根 （B）两根异号且正根绝对值大于负根绝对值

（C）有两个负实数根 （D）两根异号且负根绝对值大于正根绝对值

2．关于x的一元二次方程k(x²-2x+1)-2x²+x=0有两个实数根，则k的取值范围是（ ）

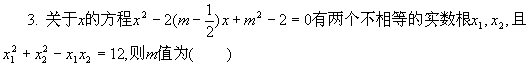
（A）m=1或m=5 (B)m=-1或m=5 (C)m=5 (D)m=-1

4．根据一元二次方程根与系数的关系判别以下各组数据哪组是方程

（A）x₁=2,x₂=-4 (B) x₁=-2,x₂=--4 (C) x₁=-2,x₂=4 (D)以上答案都不对

5．关于x的一元二次方程ax²+bx+c=0(a≠0)两根之比为1：2，则a,b,c的关系式是（ ）

（A）9ac=-10b² （B）9ac=2b （C）8ac=b² （D）9ac=2b²

6．方程x²-7x-9=0的两根为x₁,x₂,且x₁>x₂，则x₁-x₂=( )

7．方程2x²-(m-2)x-m=0的两根互为相反数，则m=（ ）

（A）0 （B）-2 （C）2 （D）-2或0

8．若矩形的长和宽是一元二次方程4x²-12x+3=0的两根，则矩形的周长、面积分别为（ ）

9．一元二次方程ax²+bx+c=0(a≠0)的一根小于1，另一根大于1，则a+b+c（ ）

A．大于0 （B）小于0 （C）任意实数 （D）只能是大于0或小于0

10．对于一元二次方程ax²+bx+c=0(a≠0)下列各命题中，真命题的个数（ ）

①当a=c时，方程两根互为倒数 ②当c=0时，方程两根均为0

③当b=0时，方程两根互为相反数④当a,c异号时，方程必有两实数根

A．1 （B）2 （C）3 （D）4

三、解答题：

1．已知方程2x²-7x+2=0的两个根为x₁,x₂,，不解方程求以下各式的值：

2．已知方程x²+(2m+1)x+m²-2=0的两根平方和等于11，求m的值

　

　

3．已知关于x的方程x²-4x+a=0有两个实数根，且一根大于1，另一根小于1，求a的取值范围。

　

　

4．已知方程2x²+4x-5=0,不解方程，求作一元二次方程，使其一根为已知方程的两根的平方和，另一根为已知方程的两根的倒数和。

　

　

　

四、列方程解应用题：

某服装厂去年1月份产量为5000件，以后每月比上月产量提高相同的百分率，且3月份比2月份的产量多1200件，求平均每月产量的增长率。

　

　

　

试卷分析

一、填空：

1．-3

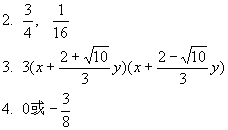
5．-8

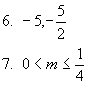
解：设x²-x+m=0的两根为x₁，x₂

∴（x₁+x₂）²-4x₁x₂<1

∴1-4m<1

-4m<0

m>0

∵Δ≥0

∴1-4m≥0

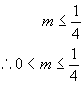
8．　　　　3

（x²+y²+1）(x²+y²)=12

(x²+y²)²+(x²+y²)-12=0

(x²+y²-3) (x²+y²+4)=0

x²+y²=3或x²+y²=-4(舍)

9． 3

2x(kx-4)-3x²+6=0

(2k-3)x²-8x+6=0

∵Δ<0

∴64-24（2k-3）<0

8-3(2k-3)<0

8-6k+9<0

6k>17

∴k的最小整数值是3

10． 0

∵x²+(m+1)x+m²+m=0有一根为0

∴m²+m=0

m(m+1)=0

m=0或m=-1

当m=-1时原方程为x²=0,x₁=x₂=0与已知矛盾

∴m=0

二、1（D）

解：设ax²+bx+c=0的两个根分别为α，β又a>0,b>0,c<0

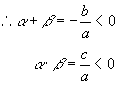
∵Δ=b²-4ac>0

∴方程有两个异号实根，且负根绝对值大

2．（D）

k(x²-2x+1)-2x²+x=0

(k-2)x²+(1-2k)x+k=0

由已知Δ≥0且k-2≠0

∴（1-2k）²-4k(k-2) ≥0

又k-2≠0 ∴k≠2

3．（D）

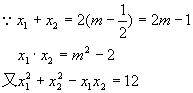
∴(x₁+x₂)²-3x₁x₂=12

(2m-1)²-3(m²-2)=12

4m²-4m+1-3m²+6-12=0

m²-4m-5=0

(m+1)(m-5)=0

m₁=-1 m₂=5

∵Δ>0

当m=-1时 x²+3x-1=0 Δ>0

当m=5时 x²-9x+23=0 Δ<0舍

∴m=-1

4．(D)

5．（D）

解：设ax²+bx+c=0的两根为β，2β

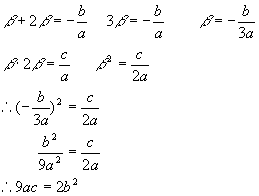
6．（D）

∵x₁>x₂

x₁+x₂=7 x₁·x₂=-9

7．（C）

∵2x²-(m-2)x-m=0的两根互为相反数

∴x₁+x₂=0

∴m-2=0 m=2

∵当m=2时 Δ>0

∴m=2

8．（C）

设4x²-12x=3=0的两根为a，b

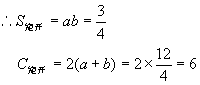
9．（D）

设方程两根为x₁，x₂

由已知（x₁-1）(x₂-1)<0

∴x₁x₂-(x₁+x₂)+1<0

当a>0时

c+b+a<0

当a<0时

c+b+a>0

10．（C）

三、解答题：

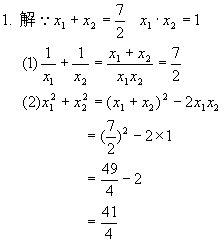
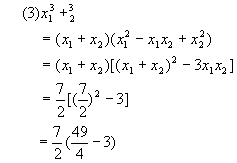
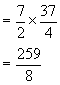
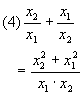
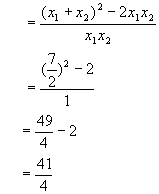
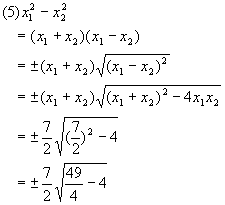
2．解：设x₁，x₂是方程的两个根

∴x₁+x₂=-(2m+1) x₁x₂=m²-2

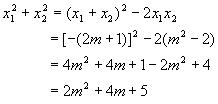
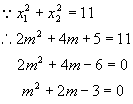
(m-1)(m+3)=0

m₁=1 m₂=-3

∵Δ=（2m+1）²-4(m²-2)

=4m²+4m+1-4m²+8

=4m+9

当m=-3时，Δ<0

当m=1时，Δ>0

∴m=1

3．解：设方程两根为x₁，x₂

∴x₁+x₂=4 x₁x₂=a

由已知（x₁-1）(x₂-1)<0

x₁x₂-( x₁+x₂)+1<0

a-4+1<0

a-3<0

a<3

∵Δ>0

∴16-4a>0

-4a>-16

a<4

∴a<3

4．解：设2x²+4x-5=0的两根为x₁x₂

所求方程两根为α、β

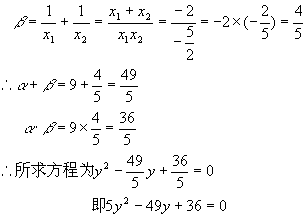
四

解：设平均每月产量的增长率为x

5000（1+x）²-5000(1+x)=1200

5000(1+x)(1+x-1)=1200

25(1+x)x=6

25x²+25x-6=0

(5x-1)(5x+6)=0

∴x=0.2=20%

答：平均每月增长率为20%

　

科目：几何 年级：初二 教师：袁爽

2001-2002第二学期第十二周

天津益中学校2001-2002学年度第二学期期中检测

八年几何试卷

一．填空：

1．等腰梯形的一腰长为2cm，一底为5cm，且一钝角为120⁰，这个等腰梯形的周长为_______．

2．等腰三角形两条中位线长分别为3和5，则它的周长为_______．

3．只有两个角相等的梯形是_______．

4．在梯形ABCD中，AD∥BC，中位线EF=4cm，EF与两条对角线的交点间的线段为GH=4cm，则下底BC的长为_______．

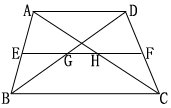
5．在等腰梯形ABCD中，AD∥BC，AB=DC，对角线AC⊥BD，并且梯形ABCD的面积为100cm²，那么梯形对角线长为_______．

6．已知三角形各边分别为6cm，8cm，10cm，那么连结各边中点所成的三角形的最长边上的高为_______．

7．线段x,y,z的第四比例项为_______．

9．如果线段a=5,b=10,c=12,那么b,a,c的第四比例项d=_______.

10.在ΔABC中，a:b:c=4:5:6，那么三条边上的高h₁,h₂,h₃的比为_______．

二．选择：

1．四边形ABCD中，AB=DC，AC=BD则四边形是（ ）

（A）平行四边形 （B）等腰梯形 （C）矩形 （D）矩形或等腰梯形

2．下面四个命题中正确的有（ ）个

①梯形的两腰之和大于两底之差 ②有两个角相等的梯形是等腰梯形

③梯形中可能有三条边彼此相等 ④梯形中必有两个锐角和两个钝角

（A）1 （B）2 （C）3 （D）4

3．下列四边形各边中点连线为菱形的是（ ）

（A）平行四边形 （B）菱形 （C）矩形 （D）直角梯形

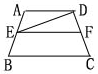
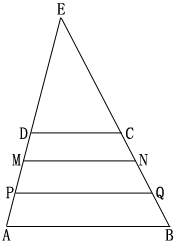
4．在梯形ABCD中，DC∥MN∥PQ∥AB，DM=MP=PA，且DC=2，AB=3.5，则MN，PQ的

长为（ ）

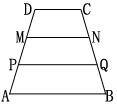
5．ΔABC∽ΔA’B’C’，且相似比为K（K≠1），那么K等于（ ）

（A）A’B’：AB （B）AB:A’B’

（C）∠A:∠A’ （D）S_ΔABC:S_{ΔA’B’C’}

6．线段AB的长为1，C是AB上一点，AC>BC，且AC是AB和BC的比例中项，则BC的长为（ ）

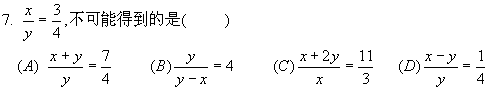
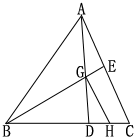
8．在ΔABC中，D是BC上一点，且BD：DC=3：1，E为 AC上一点，AD与BE交于G，AG=GD，则BG：GE为（ ）

（A）7：1 （B）5：1 （C）6：1 （D）5：2

三．判断：

1．梯形的中位线一定平分梯形的对角线．（ ）

2．梯形的中位线长能与它的一条底边长相等．（ ）

3．经过梯形一腰的中点的直线必平分另一腰．（ ）

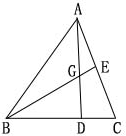
4．梯形ABCD中，AD∥BC，EF为中位线，S_ΔDBF=15cm²,则S_梯形ABCD=30cm²．（ ）

四．作图题：（尺规作图，保留作图痕迹，不写作法）

已知：线段a,b,c,d

求：梯形ABCD，使AD∥BC，AB=a,BC=b,CD=c,AD=d.

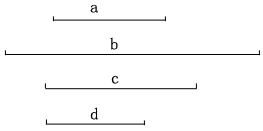
五．解答题：

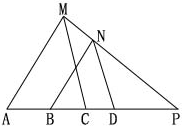
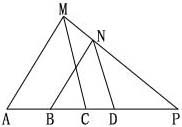
1．已知：在ΔAPM中，AM∥BN，CM∥DN，求证：PA·PD=PC·PB．

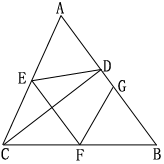
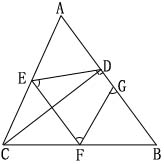
2．已知：在ΔABC中，CD⊥AB于D，E、F、G分别为AC，CB，AB中点，

求证：∠DEF=∠FGB．

3．已知：一个梯形的四条边的长分别为1，2，3，4，求这个梯形的面积．

（请你画出图形并进行计算）

　

　

　

试卷分析：

一．填空：

1．12cm或16cm

注意：两解题，分上底为5cm和下底为5cm两种情况，

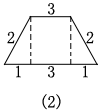
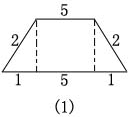
如图（1）当上底为5cm时，周长为16cm．

如图（2）当下底为5cm时，周长为12cm．

2．26cm或22cm

也是两解题

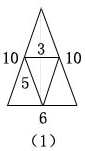
如图（1）当有一条中位线是3 cm，另二条中位线是5 cm时，周长为26 cm．

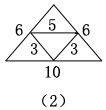
如图（2）当有二条中位线是3 cm，另一条中位线是5 cm时，周长为22 cm．

3．直角梯形

4．18 cm

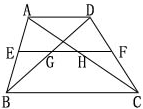
由已知EF=14，GH=4且EG=HF

∴EH=5+4=9

BC=2EH=18

如图，作DE∥AC交BC延长线于E，

由已知ΔBDE为等腰直角三角形

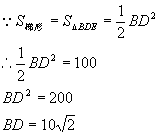
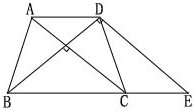
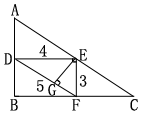
解：如图

∵AB=6，BC=8，AC=10

∴EF=3，DE=4，DF=5

∴ΔDEF为RtΔ．

最长边DF=5，

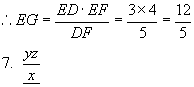
9． 6

10．15：12：10

二．选择：

1．D

2．B

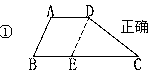
如图作DE∥AB交BC于E

∵在ΔDEC中，DE+DC>EC

∴梯形两腰之和大于两底之差．

②错误

反例：直角梯形中有两个角是直角．

③正确

上底和腰相等的等腰梯形三条边彼此相等．

④错误

反例：直角梯形

3．C

对角线相等的四边形各边中点连线是菱形

对角线互相垂直的四边形各边中点连线是矩形

4．B

如图 分别延长AD、BC交于E

∵DC=2，AB=3.5 DC∥AB

设DE=4x则AE=7x，AD=3x

∴DM=MP=PA=x

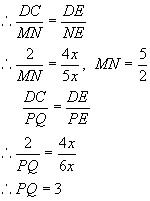
5．B

6．D

7．D

8．A

如图

作GH∥AC交BC于H

∵AG=DG，∴DH=HC

设DH=HC=a

∴BD=6a

∴BH=7a

∵GH∥EC

三．1．（√）

2．（×）

3．（×）

经过梯形一腰中点且与底边平行的直线必平分另一腰．

4．（×）S_梯形ABCD=60 cm²

5．（√）

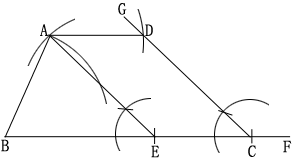
四．

1．在射线BF上截取BC=b，在射线CB上截取CE=a，则BE=b-a

2．以B为圆心，a为半径画弧，与以E为圆心，c为半径的弧交于点A

3．作CG∥EA

4．以A为圆心，d为半径画弧交CG于D，连结AD，则梯形ABCD即为所求．

五．

1．证明：

∵AM∥BN

∵CM∥DN

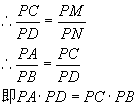
2．证明：

∵CD⊥AB

∴ΔACD为Rt三角形

∵E为AC中点

∵F、G分别为CB、AB中点，

∴FG为ΔACB中位线

∴DE=FG

∵EF∥AB

FG与ED不平行

∴EFGD为梯形

∵DE=GF

∴EFGD为等腰梯形

∴∠DEF=∠EFG

∵∠EFG=∠FGB

∴∠DEF=∠FGB

3．解：由于梯形两底之差小于两腰之和，而大于两腰之差，∴只有1、4作底，2、3作腰时才能构成梯形．

如图：梯形ABCD中，AD∥BC AD=1 AB=2 BC=4 CD=3

作DE∥AB交BC于E

∴ABED为平行四边形

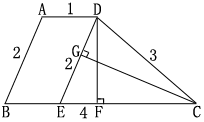∴DE=AB=2

EC=BC-AD=3

∴ΔDEC为等腰三角形．

作CG⊥DE于G，DF⊥EC于F

∵CD=CE=3，DE=2

∴DG=EG=1