第六章证明水平测试
一、试试你的身手(每小题3分,共24分)
1.举出反例说明“如果![]() ,那么点
,那么点![]() 是
是![]() 的中点”是个假命题: .
的中点”是个假命题: .
2.把命题“对顶角相等”改写成“如果…,那么…”的形式 .
3.![]() 的三个外角度数比为3∶4∶5,则它的三个内角度数分别为.
的三个外角度数比为3∶4∶5,则它的三个内角度数分别为.
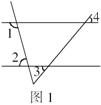
4.如图1所示,![]() ,若
,若![]() ,则
,则![]() .
.
 | |||
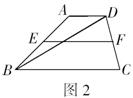 | |||
5.如图2所示,![]() ,
,![]() ,则
,则![]() .
.
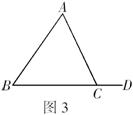
6.如图3所示,![]() 中,
中,![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
 | |||
 | |||
7.在![]() 中,
中,![]() 和
和![]() 的平分线交于点
的平分线交于点![]() ,若
,若![]() ,则
,则![]() .
.
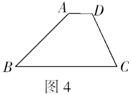
8.如图4,![]() ,
,![]() ,
,![]() .则
.则![]() 与
与![]() 的度数和是 .
的度数和是 .
二、相信你的选择(每小题3分,共30分)
1.下列语句是命题的是( )
A.你吃过午饭了吗?
B.过点![]() 作直线
作直线![]()
C.同角的余角相等
D.红扑扑的脸蛋
2.下列命题是真命题的是( )
A.同旁内角互补
B.直角三角形的两锐角互余
C.三角形的一个外角等于它的两个内角之和
D.三角形的一个外角大于内角
3.命题“垂直于同一条直线的两条直线互相平行”的条件是( )
A.垂直
B.两条直线
C.同一条直线
D.两条直线垂直于同一条直线
4.已知![]() 的三个内角度数比为2∶3∶4,则这个三角形是( )
的三个内角度数比为2∶3∶4,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
5.如果![]() 和
和![]() 的两边互相平行,则
的两边互相平行,则![]() 和
和![]() ( )
( )
A.相等 B.互补 C.相等或互补 D.无法确定
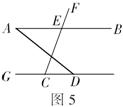
6.如图5,下列条件中,不能判定直线![]() 的是( )
的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
 | |||
 | |||
7.如图6,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() 的关系为( )
的关系为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.轮船航行到![]() 处时,观测到小岛的方向是北偏西35°那么同时从小岛观测到轮船的方向是( )
处时,观测到小岛的方向是北偏西35°那么同时从小岛观测到轮船的方向是( )
A.南偏西35° B.北偏西35° C.南偏东35° D.南偏55°
9.两条直线被第三条直线所截,则有( )
A.同位角相等 B.内错角相等
C.同旁内角互补 D.以上结论都不对
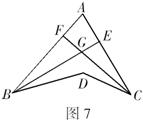 10.如图7,已知
10.如图7,已知![]() 是
是![]() 的角平分线,
的角平分线,![]() 是
是![]() 的角平分线,
的角平分线,![]() 、
、![]() 交于
交于![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的大小是( )
的大小是( )
A.70° B.75° C.80° D.85°
三、挑战你的技能(本大题共54分)
1.(9分)如图8,已知![]() 中,
中,![]() ,
,![]() ,垂足为
,垂足为![]() ,求
,求![]() 的度数.
的度数.
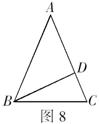 |
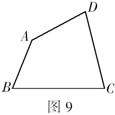
2.(9分)图9所示为一大型四边形广告牌,此广告牌要求![]() 、
、![]() 两边所在直线成
两边所在直线成
30°角,![]() 、
、![]() 两边所在直线成20°角.你能通过测量∠A、∠B、∠C、∠D的度数来检测制成的广告牌是否符合要求吗?若不能,说明理由;若能检测,说明具体的操作步骤.
两边所在直线成20°角.你能通过测量∠A、∠B、∠C、∠D的度数来检测制成的广告牌是否符合要求吗?若不能,说明理由;若能检测,说明具体的操作步骤.
 |
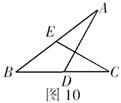
3.(9分)如图10,![]() .求证:
.求证:![]() .
.
 |
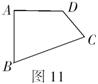
4.(9分)如图11,四边形![]() 中,请你利用“三角形内角和定理”证明“四边形的内角和等于360°”.
中,请你利用“三角形内角和定理”证明“四边形的内角和等于360°”.
 |
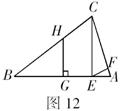
5.(9分)如图12,![]() ,
,![]() ,
,![]() 于
于![]() .求证:
.求证:![]() .
.
 |
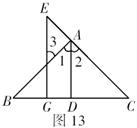
6.(9分)已知:在图13中,![]() 于
于![]() ,
,![]() 于
于![]() ,且
,且![]() .
.
求证:![]() 平分
平分![]() .
.
 |
四、拓广探索(本题12分)
四边形是大家最熟悉的图形之一,我们已经发现了它的许多性质,只要善于观察,乐于探索,我们还会发现更多的结论.
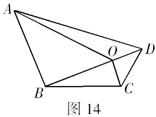
(1)如图14中,四边形一条对角线上任意一点与另外两个顶点的连线,将四边形分成四个三角形,其中相对的两个三角形的面积之积相等.你能证明这个结论吗?试试看,已知:在四边形![]() 中,
中,![]() 是对角线
是对角线![]() 上任意一点.求证:
上任意一点.求证:![]() ;
;
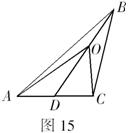
(2)如图15,在![]() 中,你能否归纳出类似的结论?若能,写出你猜想的结论,并证明,若不能,说明理由.
中,你能否归纳出类似的结论?若能,写出你猜想的结论,并证明,若不能,说明理由.
 | |||
 | |||
《证明(一)》水平测试题参考答案
一、1.略
2.如果两个角是对顶角,那么这两个角相等
3.90°,60°,30°
4.50°
5.30°
6.60°,65°
7.120°
8.160°
二、1.C 2.B 3.D 4.A 5.C 6.B 7.D 8.C 9.D 10.C
三、1.解:设![]() ,依题意,有
,依题意,有![]() .
.
解这个方程,得![]() .所以
.所以![]() .
.
在![]() 中,
中,
![]() .
.
2.答:能检测.
检测:![]() ,此时
,此时![]() 两直线的夹角为30°.
两直线的夹角为30°.
检测:![]() ,此时
,此时![]() 两直线的夹角为20°.
两直线的夹角为20°.
依据三角形内角和为180°.
3.因为![]() ,
,
又因为![]() ,
,
所以![]() .
.
4.连接![]() .因为
.因为![]() ,
,![]() ,
,
所以![]() .
.
所以![]() .
.
所以![]() .
.
即四边形![]() 的内角和等于360°.
的内角和等于360°.
5.证明:因为![]() .(已知),
.(已知),
所以![]() .(同位角相等,两直线平行)
.(同位角相等,两直线平行)
所以![]() .(两直线平行,内错角相等)
.(两直线平行,内错角相等)
因为![]() ,(已知)
,(已知)
所以![]() .(等量代换)
.(等量代换)
所以![]() .(同位角相等,两直线平行)
.(同位角相等,两直线平行)
所以![]() .(两直线平行,同位角相等)
.(两直线平行,同位角相等)
因为![]() ,(已知)
,(已知)
所以![]() .(垂直的定义).
.(垂直的定义).
所以![]() .(垂直的定义)
.(垂直的定义)
6.证明:∵![]() ,
,![]() ,(已知)
,(已知)
∴![]() .(同垂直一直线的两直线平行)
.(同垂直一直线的两直线平行)
∴![]() ,(两直线平行,同位角相等)
,(两直线平行,同位角相等)
![]() .(两直线平行,内错角相等)
.(两直线平行,内错角相等)
又∵![]() ,(已知)
,(已知)
∴![]() .(等量代换)
.(等量代换)
∴![]() 平分
平分![]() (角平分线定义).
(角平分线定义).
四、(1)证明:过点![]() 作
作![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,
,![]() ,
,
则![]() ,
,
所以![]() ,
,
![]() ,
,
因此![]() ;
;
(2)能.猜想的结论是![]() .
.
证明:过点![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于
于![]() .则
.则![]() ,所以
,所以![]() ,
,
![]() .
.
因此![]() .
.