初二（下）数学第一学月检测

数  学　试　卷

　　　　　　　　　　  考号：　　　　  姓名：　　　　  成绩：　　　　 

（本卷满分100分，考试时间：120分钟）

一、选择题（每小题2分，共24分）

1、若＞1，在下面四组数中，能组成直角三角形的是（　　）

A、、、　　　　　　  B、、、

C、、、　　　　　　　　　  D、、、

2、一个自然数的算术平方根是，则与这个自然数相邻的下一个自然数的平方根是（　 ）

　　A、　　　　  B、　　　　  C、　　　　D、

3、下面结论正确的是（　　）

 A、无限小数是无理数　　　　　　　　　　 B、无理数是开方开不尽的数

 C、带根号的数是无理数　　　　　　　　　 D、无限不循环小数是无理数

4、如图，已知矩形ABCD，R、P分别是DC、BC上的点，E、F分别是AP、RP的中点，当P在BC上从B向C移动而R不动时，那么下列结论成立的是（　　 ）

A、线段EF的长逐渐增大　 　　　　　　 B、线段EF的长逐渐减小

C、线段EF的长不改变　　　　　　　　  D、线段EF的长不能确定

　　

5、一张直角三角形的纸片，像图中那样折叠，使两个锐角顶点A、B重合，若∠B＝30⁰，AC＝，则折痕DE的长等于（　　）

　　A、　　　　　　  B、　　　　　　  C、1　　　　　　  D、

6、如图，在四个正方形拼接成的图形中，以这十个点中任意三点为顶点，共能组成（　　）个等腰直角三角形。

　　A、18　　　　　  B、22　　　　　　　  C、24　　　　　　　  D、26

7、三角形的三条边分别为－1，，＋1，则的取值范围是（　　　）

　　A、＞0　　　　 B、＞2　　　　  C、1＜＜3　　　　  D、＞3

8、在△ABC中，∠A＝∠B－∠C，则此三角形为（　　  ）三角形

A、直角　　  B、钝角　　 C、锐角　　　 D、以上三种情况都有可能

9、下列说法正确的是 (　　 )

A、的平方根是－1　　　　　　　　　 B、6是的算术平方根

C、的立方根为－2　　 　　　　　　  D、0.4是－0.064的立方根

10、若0＜＜1，则、、、这四个数中（　　）

A、最大，最小　　　　　　　　　　  B、最大，最小　　

C、最大，最小　　　　　　　　　  D、最大，最小。

11、已知：，，则的值是（　　）

A、 0.0140　　　　B、 0.1410　　　　 C、 4.459　　　　D、0.4459

12、若3＜＜4，那么的结果是（　　）

　　A、 7＋2　　　　 B、 2－7　　　　  C、 7－2　　　D、 －1－2

二、填空题（每小题2分，共20分）

13、已知线段AB＝4，BC＝3，那么线段AC的长度的取值范围是　　　　　  。

14、的平方根是　　　　，＝　　　　 。

15、当＝　　　时，最简二次根式和是同类二次根式。

16、若＜1，化简：　　　　 。

17、如果多项式因式分解的结果是，那么的值是__________。

18、已知：，则　　　　 。

19、在实数范围内分解因式：³－2＝　　　　　　　　　　　  。

20、比较大小：。

21、若，则用含有的代数式表示为 　　　 。

22、已知：；；……；若　（、为正整数）请推测：＝　　　　　＝　　　 。

三、计算下列各题：（每小题5分，共15分）

（23）

 

 

 

 

 

 

 

 

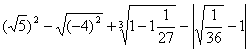
（24）

 

 

 

 

 

 

 

 

 

 

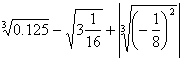
（25）

 

 

 

 

 

 

四、解答下列各题（每小题8分，共16分）

26、如图，在四边形ABCD中，AB＝3cm，CD＝2cm，∠BAD＝60⁰，∠CDA＝∠CBA＝90⁰，求四边形ABCD的面积。

 

 

 

 

 

 

 

 

 

27、为了营造人与自然和谐共处的生态环境，某市近年加快实施城乡绿化一体化工程，创建国家城市绿化一体化城市。某校甲、乙两班师生前往郊区参加植树活动。已知甲班每天比乙班少种10棵树，甲班种150棵树所用的天数比乙班种120棵树所用的天数多2天。求甲、乙两班每天各植树多少棵？

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

五、探索与证明：（28、29题各5分，30题7分，共17分）

28、如图，AD是△ABC中BC边上的中线，∠ADC为锐角，把△ADC沿直线AD折过来，点C落在点E的位置上。试猜想直线BE与直线DA的位置关系，并证明你的猜测。

 

 

 

 

 

 

 

 

29、在△ABC中，AB＝AC，∠BAC＝90°，D是BC上任意一点 。

（1）读语句画图（保留作图痕迹，不写画法）：①把△ABD沿着AD对折，得到△ADF，画出对折后的△ADF；

②翻折AC，使AC与AF叠合，折痕与BC交于点E，画出折痕AE，连接EF；

 

（2）翻折后点C与点F是否重合？猜想△DEF是什么三角形？

 

（3）证明你的结论。

 

 

 

 

 

 

 

30、如图：在Rt△ABC中，AB＝AC，∠BAC＝90°，O为BC的中点。

（1）写出点O到△ABC的三个顶点 A、B、C距离的关系；

（2）如果点M、N分别在线段AB、AC上移动，移动中保持AN＝BM，请判断△OMN的形状，并证明你的结论。

 

六、阅读理解题：（8分）

31、十六大提出全面建设小康社会。国际上常用恩格尔系数（记作）来衡量一个国家和地区人民生活水平的状况，它的计算公式为：

家庭类型	贫困	温饱	小康	富裕	最富裕
	＞60％	50％＜≤60％	40％＜≤50％	30％＜≤40％	≤30％

根据上述材料，解答下列问题：

某校初三学生对我市一个乡的农民家庭进行抽样调查。从1997年至2002年间，该乡每户家庭消费支出总额每年平均增加500元，其中食品消费支出总额每年平均增加200元。1997年该乡农民家庭平均刚达到温饱水平，已知该年每户家庭消费支出总额平均为8000元。

（1）1997年该乡平均每户家庭食品消费支出总额为多少元？

（2）设从1997年起年后该乡平均每户的恩格尔系数为（为正整数）。请用的代数式表示该乡平均每户当年的恩格尔系数，并利用这个公式计算2003年该乡平均每户的恩格尔系数（百分号前保留整数）。

（3）按这样的发展，该乡将于哪年开始进人小康家庭生活？该乡农民能否实现十六大提出的2020年我国全面进人小康社会的目标？

 

 

 

 

 

初二数学参考答案

一、选择题：

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	B	D	D	C	C	C	B	A	C	A	D	B

二、填空题：

13、1≤AC≤7；14、，；15、；16、1；17、－1；18、；

19、；20、＜；21、或；22、＝8，＝63

三、计算下列各题：

23、解：原式＝＝

24、解：原式＝＝－1

25、解：原式＝＝

四、解答下列各题：

26、解：延长AD、BC相交于点E，在Rt△ABE中

　　　　∵∠A＝60⁰∴∠E＝30⁰

又∵EB＝AB·tan A　 ED＝DC·cotE

　∴EB＝3·tan 60⁰＝　　　 ED＝2·cot30⁰＝

　∴＝－

　　　　　　 ＝

　　　　　　 ＝

　　　　　　 ＝

27、解：设甲班每天植树棵，那么乙班每天植树棵，由题意得：

整理得：

再化简得：

分解因式得：

＝30，＝－25（不符题意舍去）

经检验：＝30是原方程的根。

当＝30时，＝40

　　　答：甲班每天植树30棵，乙班每天植树40棵。

28、解：猜想BE∥DA

　　　　证明：由题意知∠1＝∠2，DC＝DE＝DB

∴∠E＝∠EBD

　　　　　  又∵∠1＋∠2＝∠E+∠EBD（∠EDC是△EBD的外角）

∴∠1＝∠E

∴BE∥DA

　　

29、解（1）如上图所示；

（2）翻折后点C与点F完全重合，△DEF是直角三角形；

（3）证明：①∵AB＝AC＝AF

　　　　　　 ∴AC＝AF

　　　　　  ∴翻折后点C与点F完全重合。

②∵AB＝AC，∠BAC＝90⁰

∴∠B＝∠C＝45⁰

∴∠1＝∠2＝45⁰

∴∠DFE＝90⁰

∴△DEF是直角三角形。

30、解（1）OA＝OB＝OC

（2）答：△OMN是等腰直角三角形。

证明：连结AO

　　　∵AB＝AC，OC＝OB

∴AO⊥BC，即∠AOB＝90⁰，∠CAO＝∠BAO

　　又∵∠BAC＝90⁰

∴∠CAO＝∠BAC＝45⁰

∵AC＝AB，∠BAC＝90⁰

∴∠B＝45⁰

∴∠NAO＝∠B＝45⁰

　　　　  又∵AN＝BM，OA＝OB

∴△AON≌△BOM

∴OM＝ON

∴∠1＝∠3

∴∠1＋∠2＝∠3＋∠2

即∠NOM＝∠AOB＝90⁰

∴△OMN是等腰直角三角形。

31、解（1）8000×60％＝4800（元）

（2）　　即

　　当＝2003－1997＝6时，≈0.55＝55％

（3）由题意得：≤50％

　　解得：≤16

　　∵1997＋16＝2013＜2020

　　∴2013年该村进入小康家庭生活，并能实现十六大提出的目标。