初二数学第一次质量调研
一、选择题
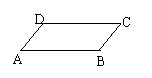
1、如图已知ABCD是平行四边形，下列结论中，不一定正确的是（ ）
A、AB＝CD B、AC＝BD
C、当AC⊥BD时，它是菱形 D当∠ABC＝90°时，它是矩形
2、一个四边形的四个内角之比为1∶2∶3∶4，则这个四边形的最大内角为（ ）
A、75° B、210° C、126° D、144°
3、顺次连结等腰梯形各边中点所构成的四边形是（ ）
A、平行四边形 B、菱形 C、矩形 D、等腰梯形
4、△ABC中，DE∥FH∥BC，AD＝DF＝FB，DE＝2，则BC＝（ ）
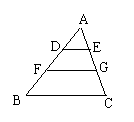A、4 B、6 C、8 D、16
 | |||
 | |||
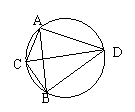
5、如图，四边形ABCD内接于圆，图中相等的圆周角共有（ ）对
A、8 B、6 C、4 D、2
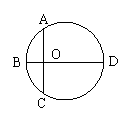6、“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题：“今有圆材，埋在壁中，不知大小以锯锯之，深一寸，锯道长一尺，问径几何？”用数学语
言可表述为：“如图，CD为⊙O的直径，弦AB⊥CD于E，CE＝
1寸，AB＝10寸，则直径CD的长为（ ）
A、12.5寸 B、13寸 C、25寸 D、26寸
7、将矩形的纸片折一次，使得折痕平分这个矩形
的面积，则这样的折纸方法共有（ ）
A、1种 B、2种 C、4种 D、无数种
8、用两个全等的直角三角形拼下列图形：①平行四边形（不包括菱形
、矩形、正方形）②矩形③菱形④正方形⑤等腰三角形，一定可以拼成的图形是（ ）
A、① B、②③⑤ C、①④⑤ D、①②③
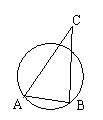
9、如图，某航道上有一暗礁，两灯塔A、B的距离恰好为暗礁分布区
圆的半径，要使船不进入暗礁处，航行中∠ACB应保持（ ）
A、大于60° B、小于60° C、大于30° D、小于30°
10、下列命中，（1）正三角形既是中心对称图形又是轴对称图形且有三条对称轴 （2）矩形既是中心对称图形又是轴对称图形且有4条对称轴 （3）对角线相等的梯形必是等腰梯形 （4）菱形的对角线的平方和等于边长的4倍，其中真命题的个数有 （ ）
A、1个 B、2个 C、3个 D、4个
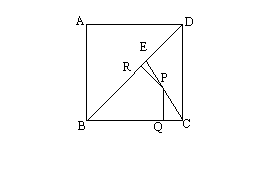
11、如图，E是边长为1的正方形ABCD的对角线BD上一点，
且BE＝BC，P为CE上任意一点，PQ⊥BC于点R，
则PQ＋PR的值是（ ）
A、
B、
C、
D、
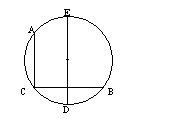12、如图，DE是⊙O的直径，弦BC⊥AC，则1）CD＝BD，2）CD＝AE，
3）EAC＝DCA＝BE，4）AB是⊙O的直径，其中正确的有（ ）
A、4个 B、3个 C、2个 D、1个
二、填空题
1、
四边形的一个内角为60°，则与它相邻内角的度数为
2、 如图已知AD∥BC，要使四边形ABCD为平行四边形，需要增加条件
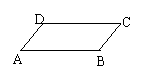（只需填一个你认为正确的条件即可）
3、
|
＝ ，ADC＝ 度。
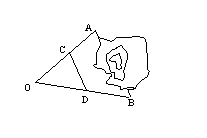4、要测量A、B两点间距离，在O点设桩，取OA中点C、OB中点D，测得CD＝31.4 m，则AB＝ m。
5、矩形ABCD中，对角线AC＝10 cm ，∠CAB＝2∠ACB，BE⊥AC于E，
则BE＝ cm，AE＝ cm。
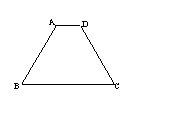
6、已知，如图等腰梯形ABCD，AD∥BC，∠B＝60°，
AD＝15，AB＝45。则BC＝
7、菱形ABCD中，∠ABC＝120°，对角线BD＝8 cm，则
菱形的周长为
|
|
AB刚好经过圆心，那么AB的度数为
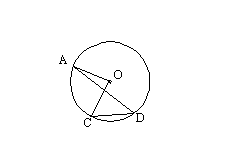
9、如图，圆心角∠AOB＝100°，则圆周角
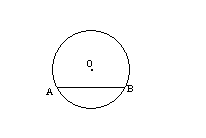
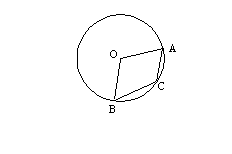∠ACB＝ 度。
 |
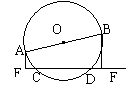10、如图，AB是⊙O的直径，CD是弦，若AB＝10 cm ，CD＝8 cm ，那么A、B两点到CD的距离之和为
11、若一个梯形内接于圆，有如下四个结论：①它是等腰梯形；②它是直角梯形；③它的对角线互相垂直；④它的对角互补；请写出正确结论的序号 （把你认为正确结论的序号都填上）。
12、已知，AB是⊙O的直径，点C、D在半圆上，且∠BAC＝20°，则∠ADC＝
25、作图题：（
（1） 已知矩形ABCD，画一个圆，使这个圆经过A、D两点，并且B、C两点在圆内。（
）
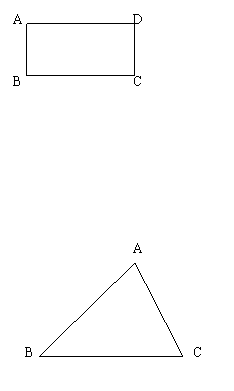
（2） 如图，△ABC是一个任意三角形，现在要从这个三角形中裁下一部分，与剩下的部分拼成一个平行四边形，请你在图中画出裁剪线（用虚线表示），简要说明裁剪线的特征，并说明怎样拼成一个平行四边形。（）
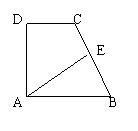
26、如图，已知直角梯形ABCD中，AD⊥AB，AB∥CD，AB=BC，AB=20cm，DC=4cm，AE⊥BC，求（1）AE的长；（2）梯形ABCD的面积。（
）
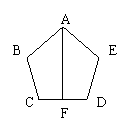
27、如图，AB=AE，∠ABC=∠AED，BC=ED，点F是CD的中点。（）
（1） 求证：AF⊥CD；
（2） 在你连结BE后，还能得出什么新的结论？请写出三个（不要求证明）
 |
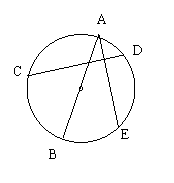
28、已知：如图，AB是⊙0的直径，弦AE⊥CD。求证：BC=ED。（
）
 |
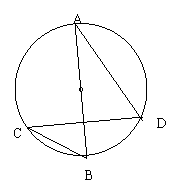
29、(1)如图，已知⊙0中，弦CD垂直于直径AB，OE⊥AD于E点，求证：BC=2OE。
（2）将上题中的“直径AB”改成“弦AB（不是直径）”，其它条件不变，结论是否仍然成立？若成立，请画出图形并且证明，不成立说明理由。（
）
 |