北师大八上一至三章习题选

第一章：

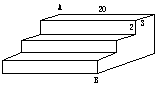1、如图是一个三级台阶，它的每一级的长宽和高分别为20dm、3dm、2dm，A和B是这个台阶两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物，则蚂蚁沿着台阶面爬到B点最短路程是_____________.

2、印度数学家什迦逻（1141年-1225年）曾提出过“荷花问题”：

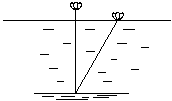“平平湖水清可鉴，面上半尺生红莲；

出泥不染亭亭立，忽被强风吹一边，

渔人观看忙向前，花离原位二尺远；

能算诸君请解题，湖水如何知深浅？”

请用学过的数学知识回答这个问题。

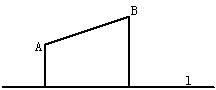3．如图，A、B是笔直公路l同侧的两个村庄，且两个村庄到直路的距离分别是300m和500m，两村庄之间的距离为d(已知d²=400000m²)，现要在公路上建一汽车停靠站，使两村到停靠站的距离之和最小。问最小是多少？

4、 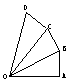 图，∠OAB=∠OBC=∠OCD=90°， AB=BC=CD=1，OA=2，则OD²=____________.

5．寒冷的冬天，你需要一杯热热的朱古力。可是在调制的过程中，老师遇到了这样一个问题：搅拌棒的长度太短了，不能搅拌到底部的饮料。已知圆柱形水杯的底面直径为5cm，高为12cm，你能帮老师计算一下搅拌棒至少要多长吗？老师新买的一根长为24cm的搅拌棒，如果设其露在杯子外面的长为hcm，你能求出h的取值范围吗？

　　　　　　　　　　　　 处理方式：1）分小组活动，动手实验。

　　　　　　　　　　　　　　　　  2）画图，并计算。

6．如图是棱长为4cm的立方体木块，一只蚂蚁现在A点，

若在B点处有一块糖，它想尽快吃到这块糖，则蚂蚁沿正

方体表面爬行的最短路程是　　　　　 cm；

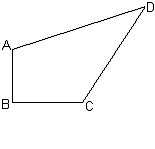
7．如图，一块草坪的形状为四边形ABCD，其中∠B=90º，AB=3m，BC=4m，CD=12m，AD=13m，求这块草坪的面积。

第二章：

1．判断正误，在后面的括号内，对的打“√”，错的画“×”。

（1）；（　）

（2）互为相反数的立方根互为相反数；（　）

（3）任何数的立方根只有一个；（　）

（4）（　）

（5）如果一个数的平方根与其立方根相同，则这个数是1；（　）

（6）如果m是n的立方根，那么m·n≥0；（　）

2．将一个体积为125cm³的铜块改铸成8个相同大小的小立方体小铜块，求每个小立方体铜块的表面积。

3．判断下列语句是否正确？在后面的括号内，对的打“√”，错的画“×”。

（1）8的立方根是。　　　　　　　　　　　　　　　　（　　）

（2）－0.001的立方根是－0.1。　　　　　　　　　　（　　）

（3）的立方根是。　　　　　　　　　　　　 （　　）

（4）64的平方根的立方根是2。　　　　　　　　　　（　　）

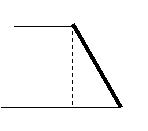4、高速公路旁有一矩形坡面，其横截面如图所示，

公路局为了美化公路沿线环境，决定把该矩形坡面

平均分成11段相间的种树与栽花。已知该矩形坡面

的长为550米，铅直高度AB为2米，水平宽度BC

为1米，若种草每平方米需投资20元，栽花每平方

米需投资15元，求公路局将这一坡面美化最少需投

资多少元？（结果保留三个有效数字）

5、把下列各数写入相应的集合中：，0.…（相邻两个2之间3的个数逐次加1）。

　　　　　  ⑴正数集合｛　　　　　　　　　　　…｝；

⑵负数集合｛　　　　　　　　　　 …｝；

⑶有理数集合｛　　　　　　　　　 …｝；

⑷无理数集合｛　　　　　　　　　 …｝

⑸整数集合｛　　　　　　　　　　 …｝；

⑹实数集合｛　　　　　　　　　　 …｝。

6、在数轴上表示下列各数：，并把它们用“＜”连接起来。你能说说实数大小比较的方法吗？

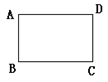7、如图1，在长方形ABCD中，AB=，BC=，则长方形ABCD的面积为多少？周长为多少？　

　　　　 

8、化简：⑴⑵，⑶，⑷，⑸，⑹。

9、的平方根是＿＿＿＿；0.216的立方根是＿＿＿＿。

10、算术平方根等于它本身的数是＿＿＿＿；立方根等于它本身的数是＿＿＿＿。

11、估算比较大小：（1）＿＿＿－3.2；（2）＿＿＿5。

12、一个正方体的体积变为原来的27倍，则它的棱长变为原来的＿＿＿＿倍。

13、的算术平方根是＿＿＿＿； 的算术平方根是＿＿＿＿。

满足的整数是＿＿＿＿。

14、如图所示，要在离地面5米处的电线杆上的两侧引拉线AB和AC，固定电线杆，生活经验表明，当拉线的固定点B（或C）与电线杆底端点D的距离为其一侧（即AB或AC）长度的时，电线杆比较稳定。现要使电线杆稳定，问拉线至少需要多长才能符合要求？试用你学过的知识进行解答。（精确到1米）

第三章：

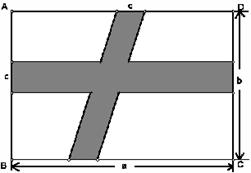
1、在矩形ABCD中，横向阴影部分是矩形，另一阴影部分是平行四边形。依照图中标注的数据，计算空白部分的面积，其中面积是________________

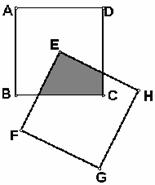
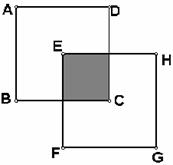
2、如图，正方形纸片ABCD和正方形EFDH边长都是1，点E是正方形ABCD的中心，在正方形EFGH绕着点E旋转过程中，

（1）观察两个正方形的重叠部分的面积是否保持不变？

（2）如果保持不变，求出它的值；否则，请简要说明理由。

 

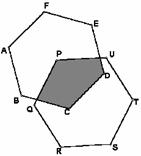
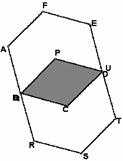
3、如图，两个全等的正六边形ABCDEF、PQRSTU，其中点P位于正六边形ABCDEF的中心，如果它们的面积均为1，则阴影部分的面积是__________。

4、一漆匠用右图所示的胶滚沿从

左到右的方向将图案滚涂到墙上，下

列给出的四个图案中，符合图示胶滚

涂出的图案是（　　 ）

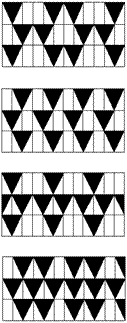
A、

B、

C、

D、

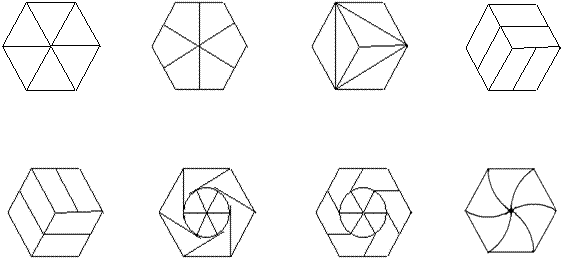
5、某地板厂要制作一批正六边形形状的地板砖，为适应市场多样化的需求，要求在地板砖上设计的图案能够把正六边形6等分，请你帮他们设计等份方案（至少设计两种）。

分析：本题是一开放式的作图题，答案不唯一。