期末数学考试总复习试题
一、填空题(3分×12=36分)
1、如果1<x<2,用不等号表示(x-1)(x-2)_______0,不等式组 的非负整数解是_____________.
的非负整数解是_____________.
2、分解因式![]() =__________,要使
=__________,要使![]() ,则x的值是____________.
,则x的值是____________.
化简![]() _____________.
_____________.
3、在比例尺1:200000的某地地图上,A、B两地相距5cm,则AB两地的实际距离是________km.
4、已知△ABC的三边之比为2:3:4与它相似的另一个△A′B′C′的最小边为8cm,则最大边应为__________cm.
5、一组数据1,2,3,3,3,4,5中,平均数![]() =_________,中位数是________,众数是____________.
=_________,中位数是________,众数是____________.
6、已知在一个样本中,50个数据分别落在5个组内;第一、二、三、四、五组数据个数分别为2,8,15,20,5,
则第四组的频数是_________,频率是______.
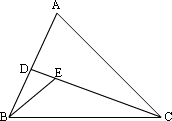
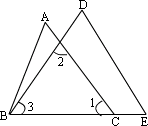
7、如图1,若A=60°,∠BEC=120°,∠EBD=25°,则∠ACD=__________.
 1
1 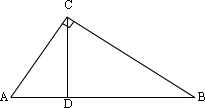 2
2 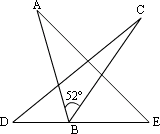 3
3
8、如图2,已知CD是Rt△ABC斜边上的高,且AD=9,BD=16,则CD=______,AC=_________, BC=____________.
9、如图3,已知∠ABC=52°,则∠A+∠C+∠D+∠E=____________.
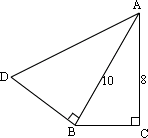
10、如图4,∠ACB=∠ABD=90°AB=10,AC=8,当AD=_______时,△ABC∽△ADB.
 4
4 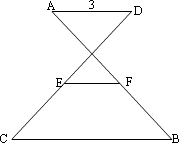 5
5  6
6
11、如图5,AD∥BC,AD=3,BC=7,E、F分别是CD、AB中点,则EF=_________.
12、如图6,E为□ABCD的边BA延长线上一点,CE交BD于F,交DA于G,则图中相似的三角形有____________对.
二、选择题(3分×12=36分,其中23、24题是多项选择)
13、已知x(y+1)-y(x-2)=2,则代数式x2+2x+4xy+4y+4y2的值是( )
A.10 B.12
C.8 D.6
14、某商店销售一批服装,每件售价250元,可获利25%,则这种服装的成本价是( )
A.180元 B.200元
C.220元 D.210元
15、甲、乙两个小组各20名同学,在同一次数学测试中,两组成绩平均数![]() 相等,但方差不同S甲2=13.2,
相等,但方差不同S甲2=13.2,
S△2=20.5,则这次测试中成绩比较整齐的组是( )
A.甲组 B.乙组
C.两组相近 D.不好比较
16、已知△ABC∽△DEF∽△GHP,且S△ABC: S△DEF:S△GHP=1:5:4则它们周长之比是( )
A.1:5:4
B.4:5:1
C.1:![]() :2 D.2:
:2 D.2:![]() :1
:1
17、下列说法不正确的是( )
A.若a∥b,b∥c,则a∥c
B.同一平面内两直线不平行就必相交
C.平面内垂直于同一条直线的两直线平行 D.同旁内角互补,两直线平行或垂直
18、张老师与李老师同时从学校出发,步行15千米去某城买书,张老师比李老师每小时多走1千米,结果比李
老师早到半小时,若设李老师每小时走x千米,依题意得方程,正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
19、下列命题中,是假命题的是( )
A.两个等腰直角三角形相似
B.两个等腰梯形相似
C.斜边和一直角边对应相等的两直角三角形相似
D.两个正方形相似
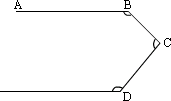
20、如图7AB∥ED,∠B+∠C+∠D等于( )
 7
7 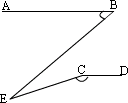 8
8 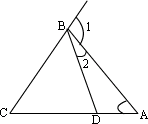 9
9
A.180° B.270°
C.360° D.450°
21、如图8,已知AB∥CD,∠B=45°,∠DCE=155°,则∠BEC等于( )
A.5° B.10°
C.15° D.20°
22、如图9,若∠BCD=∠BDC,则∠1、∠2、∠3的大小关系是( )
A.∠1=∠2+∠3
B.∠1=2∠2+∠3
C.∠1=∠2+2∠3 D.∠1+∠2+∠3=180°
23、(多项选择题)具备下列条件的三角形中,为直角三角形的是( )
A.∠A-∠B=∠C B.∠A=∠B=![]() ∠C
C.∠A:∠B:∠C=1:2:3 D.∠A-∠B=90°
∠C
C.∠A:∠B:∠C=1:2:3 D.∠A-∠B=90°
24、下列命题正确的是( )
A.m2-2mn+![]() n2不是完全平方式 B.多项式x2-2x+k2有一个因式是(x-1),则k=±1.
n2不是完全平方式 B.多项式x2-2x+k2有一个因式是(x-1),则k=±1.
C.若△ABC的三边a、b、c满足3a3+6a2b-3a2c-6abc=0,则△ABC为等腰三角形.
D.“相等的两角”是对顶角是真命题
三、解答题(25—30每题7分,31题6分,共计48分)
25、(7分)如图,已知AC∥DE,若∠ABC=70°,∠E=50°,∠D=75°,求∠A、∠ABD的度数.
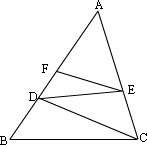
26、(7分)如图,在△ABC中,DE∥BC,EF∥DC,求证:AD2=AF·AB.
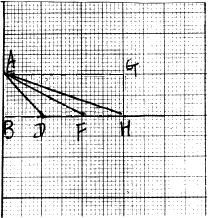
27、(7分)如图,在正方形的格纸中,连结AD、AF、AH.
(1)利用判断三角形相似的方法,说明△ADF∽△ADH. (2)试问∠AFB+∠AHB等于多少度,并说明理由.
28、(7分)若![]() ,求x的值.
,求x的值.
29、(7分)某单位要制作一批论文集,甲印刷公司提出:每本论文印刷收费20元,另收封面设计费。论文中的
插图、排版等总费用为2000元;乙印刷公司提出:每本论文信纸、纸张、印刷费30元,不收封面设计费及
其它费用。
(1)制作多少本论文集时,选择甲印刷公司比较合算?
(2)制作多少本论文集时,选择乙印刷公司比较合算?
(3)制作多少本论文集时,去两公司都一样?
30、如图所示,是某晚报“百姓热线”一周内接到热线电话的统计图.其中有关环境保护问题的电话最多,
共70个,请回答下列问题:
(1)本周“百姓热线”共接到热线电话多少个? (2)有关道路交通问题有电话有多少个?

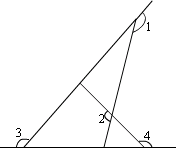
31、(6分)如图,求∠1+∠2+∠3+∠4的度数.
答案与提示:一、1、<0,1,2
2、原式![]()
x=-3 ![]()
3、10
4、答案:16
提示:设最大边长为xcm,∴![]() ,∴x=16
,∴x=16
5、3 3 3
6、答案:20 40%
提示:![]()
7、答案:35°
提示:由外角定理可得∠EDB=120°-25°=95°,
∴∠ACD=95°-60°=35°
8、答案:12 15 20
提示:利用射影定理CD2=AD·DB=9×16,
∴CD=12,
AC2=AD·AB=9×25,
∴AC=15,
BC2=BD·BA=16×25,
∴BC=20
9、答案:130°
提示:连结AC,则∠D+∠E=∠ACD+∠EAC
10、答案:12.5或![]()
提示:当∠BAC=∠BAD或∠BAC=∠BDA都相似,
所以AD=12.5或![]()
11、答案:2
提示:∵AB、CD各分成10等份
12、答案:6对
提示:△GAE∽△GDC,△FBE∽△FDC,△FDG∽△FBC,
△GAE∽△CBE,△GDC∽△ECB,△BCD∽△DAB.
二、13----17 ABACD 18----22 BBCDC 23 ABC 24 ABC
提示:
13、将条件化简为x+2y=2,代数式为(x+2y)2+2(x+2y)+2=22+2×2+2=10.
14、设成本价为x,由公式![]()
15、∵S甲2<S乙2
16、 相似三角形面积的比等于周长的平方比.
19、等腰梯形对应角相等,但对应边不一定成比例.
20、过C作CF∥AB.
21、过E作EF∥CD,利用内错角相等和同旁内角互补可得.
22、如图,(∠1+∠2)=2∠4,∠4=∠2+∠3代入上式,∴∠1+∠2=2∠2+2∠3,∴∠1=∠2+2∠3.
23、 D中,显然∠A>90°.
24、 C中,3a[a2+2ab-ac-2bc]=0,
∴3a[a(a-c)+2b(a-c)]=0,3a(a-c)(a+2b)=0
∵a>0,a+2b>0,
∴a-c=0,
∴a=c.
三、25、解:
∵AC∥DE(已知),且∠D=75°,∠E=50°(已知),
∴∠D=∠2=75°,∠E=∠1=50°(两直线平行,同位角相等),
∴∠3=180°-(∠2+∠1)=180°-(75°+50°)=55°(三角形内角和等于180°)
又∵∠ABC=70°(已知),
∴∠ABD=∠ABC-∠B=70°-55°=15°(等式性质)
在△ABC中,∠A=180°-∠ABC-∠1=180°-70°-50°=60°(三角形内角和等于180°)
26、分析:
要证明AD2=AF·AB,则转证![]() ,又A、F、D、B在同一直线上,
,又A、F、D、B在同一直线上,
要证等式左右没有直接关系,则分别考虑![]() 与哪两条线段对应成比例,
与哪两条线段对应成比例,
由平行可得到.
证明:∵EF∥CD(已知),∴∠AFE=∠ADC,∠AEF=∠ACD(两直线平行,同位角相等)
∴△AFE∽△ADC(有两角对应相等的两个三角形相似)
∴![]() (1)(两相似三角形对应边成比例)
(1)(两相似三角形对应边成比例)
同理DE∥BC,∴△ADE∽△ABC
∴![]() (2)
(2)
由(1)(2)∴![]() (等量代换)
(等量代换)
即AD2=AF·AB(比例性质)
27、(1)过A作AG∥DH,AB⊥DH,
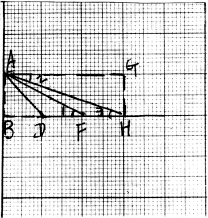
连结BD、GH,使AG为3个格点长,使AB=BG=GH为1个格点长,
在△ADF与△ADH中,
∵∠ADF=∠ADH(公共角)
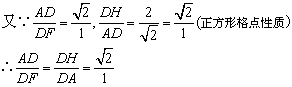
∴△ADF∽△ADH(两边对应成比例,且夹角相等的两个三角形相似)
(2)由△ADF∽△ADH可知:
∠1=∠DAH(相似三角形对应角相等)
又∠3=∠2(两直线平行内错角相等)
∴∠1+∠3=∠DAH+∠2=45°(等式性质)
即∠AFB+∠AHB=45°
28、分析:
在各分母和不为零时,可利用等比定理,但此比例式结构特殊,所以要分情况讨论:
解:
(1)当(a+b)+(b+c)+(a+c)≠0时,
![]()
(2)当a+b+c=0,则各分母之和为零,
∴a+b=-c,批它代入x中,
∴![]()
综上所述,当a+b+c≠0时,![]() 当a+b+c=0时,x=-1.
当a+b+c=0时,x=-1.
29、设制作x本论文集,且设甲印刷公司收费为y甲、乙印刷公司收费为y乙.
∴y甲=20x+2000,y乙=30x,
(1)当y甲<y乙时,2000+20x<30x,∴x>200(本)
(2)当y甲>y乙时,2000+20x>30x,∴x<200(本)
(3)当y甲=y乙时,2000+20x=30x,∴x=200(本)
答:若制作多于200本论文集时,去甲印刷公司合算,
若制作小于200本论文集时,去乙印刷公司合算,
若制作200本论文集时,去两公司都一样.
注:此题做法叫做“执果索因”法,即先从结果入手,再去找制作的本数,是数学的一种重要思维方法.
30、分析:
此题是常见的“频率分布直方图问题”,直方图是横着放置的,识图,读懂题意,善于处理信息和数据是关键.
解:
(1)根据频率=![]() ,从有关“环境保护”的热线电话为70个,又从图中对应找到频率为35%求本周的热线电话的个数就是求总体个数.
,从有关“环境保护”的热线电话为70个,又从图中对应找到频率为35%求本周的热线电话的个数就是求总体个数.
即![]() ,∴本周电话个数有
,∴本周电话个数有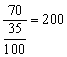 (个)
(个)
(2)同理本周“道路交通”问题的电话个数为:
200×20%=40(个)
答:本周共接到热线电话有200个,有关道路问题的电话有40个.
31、解法一:利用平角为180°求得,如图
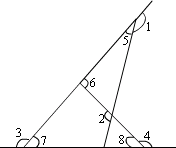
∵∠2=∠5+∠6,∠6=∠7+∠8(三角形的一个外角等于和它不相邻的两个内角和)
∴∠1+∠2+∠3+∠4=∠1+(∠5+∠6)+∠3+∠4
=(∠1+∠5)+(∠7+∠8)+∠3+∠4
=(∠1+∠5)+(∠3+∠7)+(∠8+∠4)(等式性质)
而∠1+∠5=180°,∠3+∠7=180°,∠8+∠4=180° (平角的定义)
∴∠1+∠2+∠3+∠4=3×180°=540°
解法二:利用四边形内角和为360°求得,如图
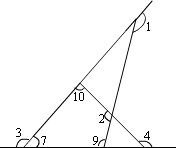
∵∠1=∠7+∠9,∠4=∠7+∠10(三角形的一个外角等于和它不相邻的两个内角和)
又∠3=180°-∠7(平角定义)
∴∠1+∠2+∠3+∠4=(∠7+∠9)+∠2+(180°-∠7)+(∠7+∠10)
=( ∠7+∠9+∠2+∠10)+180°
=360°+180°
=540°(等式性质)
还有其它多种证法,请去探索