| 数学 | |||||||
| 八年级数学第二讲 主讲教师:许桂云 | |||||||
|
| |||||||
| 内容提要: 本章教材分析 注意的几个问题 例题 巩固练习 答案 本讲正文 第十一章 二次根式 第一讲 二次根式的概念及性质 一、本章教材分析: 1、本章主要内容是二次根式的性质与运算,本章自始至终围绕着二次根式的化简与运算问题,由浅入深地讲解二次根式的有关概念及性质,从而帮助同学更好地掌握二次根式的化简与运算方法。二次根式的概念及性质是直接建立在第十章“数的开方”基础之上的,而这一章的重点——二次根式的运算,既与二次根式的概念、性质有关,又紧密联系着初一学过的整式,分式的基本运算。本章的内容一方面配合了几何课中勾股定理及其应用的学习,又直接为下一章一元二次方程的学习打下了必要基础。 2、重点、难点关键: 重点:二次根式的化简与运算 难点:正确理解与运用分式: 关键:正确认识与运用二次根式的概念及性质。 二、注意的几个问题 <一>根式的概念 1、二次根式的非负性。即 2、公式 3、 4、为减少学习困难,本章无特别说明,所有字母都表示正数。 5、公式中的条件① ③ 6、判断同类二次根式的前提条件:先把二次根式化为最简二次根式 7、一个二次根式的有理化因式可能不唯一 <二>二次根式中的隐含条件 三、例题: 例1、下列各式中,哪些是二次根式?哪些不是?
解:由二次根式定义, 例2、若a、b满足
解:∵ ①×3+②×5,得 ①×2-②×3,得 由21+5S ∴ 注意:本题应用了二次根式及绝对值的非负性质 例3、比较 解:
∵2 注意:本题应用了 例4、已知:实数a满足1992-a+ A、1991 B、1992 C、1993 D、1994 分析:由二次根式的意义,可知 ∴1992-a=a-1992 又1992-a+ ∴ 两边平方, 例5、对实数x,求 解:由二次根式意义 要使 y最大,必分母最小,而8-x最大,由于 四、巩固练习: 1、设 2、已知
3、用二次根式性质化简 4、已知: 5、设等式 6、求 答 案 1、- 3、提示: 4、当 5、 6、4 校对人:潘娜 | |||||||
| 天津名师网校版权所有 | |||||||
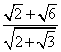 与
与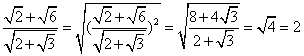
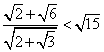
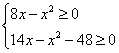 解之
解之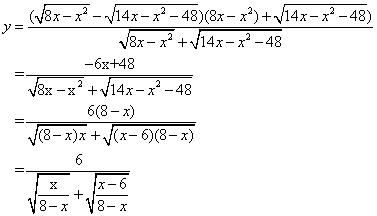
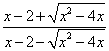 的值
的值