1.2 能得到直角三角形吗？
1、 勾股定理的逆定理
2、 勾股数
3、 勾股定理与逆定理的区别
例1判断下列三角形是否为直角三角形。
(1)在⊿ABC中，AC=12，AB=20，BC=16
(2)一个三角形三边满足a2-b2=c2
例2若⊿ABC的三边 a,b,c满足a2+ b2+ c2+338=10a+24b+26c,判断⊿ABC的形状。
例3已知正方形ABCD，E是BC的中点，F在AB上，且BF=
AB，猜想EF与DE的位置关系，并说明理由
例4已知某开发区有一块四边形的空地ABCD，现计划在空地上种植草皮，经测量，
∠A=
，AB＝3米，BC=12米，CD=13米，DA=4米，若每平方米草皮需要200元，问需要投入多少？
1.3蚂蚁怎样走最近
1. 立体图形中的勾股定理
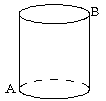
例⒈出示问题1：有一个圆柱，它的高等于12厘米，底面半径等于3厘米．在圆行柱的底面A点有一只蚂蚁，它想吃到上底面上与A点相对的B点处的食物，需要爬行的的最短路程是多少？(π的值取3)．
例2甲、乙两位探险者到沙漠进行探险.某日早晨8∶00甲先出发，他以6千米/时的速度向东行走．1时后乙出发，他以5千米/时的速度向北行进．上午10∶00，甲、乙两人相距多远？
例3如图,长方体的长BE=15cm,宽AB=10cm,高AD=20cm,点M在CH上,且CM=5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点M,需要爬行的最短距离是多少?
例4已知，如图，在⊿ABC中，∠A=，DE为BC的垂直平分线，求证：
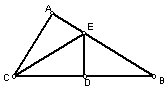
例5为了丰富少年儿童的业余生活，某社区要在如图所示AB所在的直线建一图书室，本社区有两所学校所在的位置在点C和点D处，CA⊥AB于A，DB⊥AB于B，已知AB = 25km，CA = 15 km，DB = 10km，试问：图书室E应该建在距点A多少km处，才能使它到两所学校的距离相等?
C
练习
一、填空题:
1.三角形的三边满足a2=b2+c2,这个三角形是______三角形，它的最大边是_____.
2.若一个直角三角形的三条边长是三个自然数，其中有两边的长分别为6和10，那么这个三角形的第三条边长是______.
3.三边长分别为m2-n2,2mn,m2+n2的三角形是______三角形.
4.在△ABC中，∠C=900,，BC=60cm,CA=80cm,一只蜗牛从C点出发，以每分20cm的速度沿CA-AB-BC的路径再回到C点，需要______分的时间.
二、选择题
5.如图1，已知正方形的面积为25，且AC比AB大1，BC的长为( ).
A.3 B.4 C.5 D.6
6.小刚准备测量河水的深度,他把一根竹竿插到离岸边1.5m远的水底,竹竿高出水面0.5m,把竹竿的顶端拉向岸边,竿顶和岸边的水平刚好相齐,河水的深度为( ).
A.2m B.2.5cm C.2.25m D.3m
7.三角形的三边长分别为6,8,10，它的最短边上的高为( ).图1
A.6 B.4.5 C.2.4 D.8