八年级上学期期中数学模拟试卷 (王忠2003.10)
(满分:150分,其中卷一:100分,卷二:50分; 时间:120分钟)
班级___________姓名________________座号_________成绩______________
(卷 一)
一、填空题(每小题3分,共30分):
1、现有一长5米的梯子,架靠在建筑物的墙上,它们的底部在地面的水平距离是3米,则梯子可以到达建筑物的高度是___________米。
2、5的平方根是_____,32的算术平方根是_____,-8的立方根是_____。
|
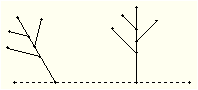
4、如图1所示,图形①经
过_______变化成图形②,图
形②经过______变化成图形③,
|
|
|
5、图2中,甲图怎样变成乙图:
|
|
6、用一根10㎝长的铁丝围成一个平行四边形
|
|
|
7、用两个一样三角尺(含30°角的那个),能拼出______种平行四边形。
8、估算:(1)![]() ≈_____(误差小于1),(2)
≈_____(误差小于1),(2)![]() ≈_____(精确到0.1)。
≈_____(精确到0.1)。
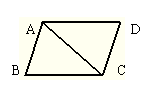 9、已知:四边形ABCD中,AB=CD,要使四边形ABCD为平行四边形,需要增加__________。(只需填一个你认为正确的条件即可)
9、已知:四边形ABCD中,AB=CD,要使四边形ABCD为平行四边形,需要增加__________。(只需填一个你认为正确的条件即可)
|
∠B=72°,则∠CAD=_________°。
|
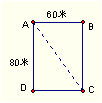
1、如图4是我校的长方形水泥操场,如果一学生要
从A角走到C角,至少走( )
A.140米 B.120米 C.100米 D.90米
2、下列说法中,正确的有( )
|
③带根号的数都是无理数; ④-2是4的一个平方根。
|
|
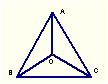
现将⊿AOB绕点O至少要旋转几度后与⊿BOC重合。( )
A. 60° B. 120° C. 240° D. 360°
4、和数轴上的点成一一对应关系的数是( )
A.自然数 B.有理数 C.无理数 D. 实数
 5、如图6所示,在
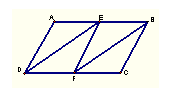
5、如图6所示,在![]() ABCD中,E、F分别AB、CD的中点,连结DE、EF、BF,则图中平行四边形共有( )
ABCD中,E、F分别AB、CD的中点,连结DE、EF、BF,则图中平行四边形共有( )
A.2个 B.4个 C.6个 D.8个
|
(1).![]() (2).
(2).![]()
(3).![]() (4).
(4).![]()
四、解答题(每题5分,共30分):
1、用计算器比较![]() 与
与![]() 大小。
大小。
![]() 解:
解:![]() 按键:
按键:
显示:_________________________________;
![]()
![]() 按键:
按键:
显示:_________________________________;
所以![]() _________
_________ ![]() ( 填“>”或“<” )
( 填“>”或“<” )
2、![]() 在数轴上画出表示
在数轴上画出表示![]() 的点。 3、把图7向右平移5格;把图8绕
的点。 3、把图7向右平移5格;把图8绕
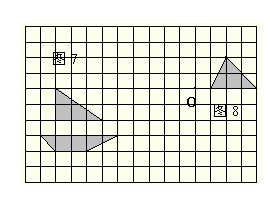 (保留作图痕迹,不写作法。)
O点逆时针旋转90°。
(保留作图痕迹,不写作法。)
O点逆时针旋转90°。
![]()
4、用大小完全相同的250块正方形
地板砖铺一间面积为40平方米的客
厅,请问每一块正方形地板砖的边
长是多少厘米?
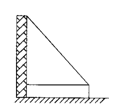 5、一高层住大厦宅发生火灾,消防车立即赶到距大厦9米处(车尾到大厦墙面),升起云梯到火灾窗口如图9,已知云梯长15米,云梯底部距地面2米,问发生火灾的住户窗口距离地面多高?
5、一高层住大厦宅发生火灾,消防车立即赶到距大厦9米处(车尾到大厦墙面),升起云梯到火灾窗口如图9,已知云梯长15米,云梯底部距地面2米,问发生火灾的住户窗口距离地面多高?
| |||
| |||
|
|
|
|
|
|
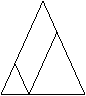 6、小明和小东经常在一块等腰三角形的草坪上玩耍,一天他们发现了一个有趣的现象:如图10草坪等腰⊿ABC,AB=AC,他们两人同在BC边上一点P,然后小明沿AC平行线PE(点E在AB上)、EA走向A处,小东沿BA的平行线PF(F点在AC上)、FA走向A处,当他两个步行速度一样时,他们同时到达A点,并且在BC边上不断改变P点位置。在步行速度一定时,
6、小明和小东经常在一块等腰三角形的草坪上玩耍,一天他们发现了一个有趣的现象:如图10草坪等腰⊿ABC,AB=AC,他们两人同在BC边上一点P,然后小明沿AC平行线PE(点E在AB上)、EA走向A处,小东沿BA的平行线PF(F点在AC上)、FA走向A处,当他两个步行速度一样时,他们同时到达A点,并且在BC边上不断改变P点位置。在步行速度一定时,
到达A处的时间也完全一样,你知道为什么吗? 说说你理由。
![]() (卷 二)
(卷 二)
一、填空题(每小题6分,共24分):
1、已知![]() ABCD的对角线AC、BD相交于点O,AC =16㎝,BD =12㎝,BC =10㎝,则⊿OAD的周长是_______,
ABCD的对角线AC、BD相交于点O,AC =16㎝,BD =12㎝,BC =10㎝,则⊿OAD的周长是_______, ![]() ABCD的面积是__________。
ABCD的面积是__________。
2、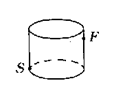
|
3、 如图11所示,圆柱形玻璃容器,高18 cm,底面周长为60 ㎝,在外侧距下底1㎝点S处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口处1㎝ 的点F处有一苍蝇,急于捕获苍蝇充饥的蜘蛛,所走的最短路线的长度是___________㎝。
4、我们把符合等式a2+b2=c2 的a、b、c三个称为勾股数。现请你用计算器验证下列各组的数是否勾股数。你能发现其中规律吗?请完成下列空格。
3,4,5;5,12,13;7,24,25;9,40,41;11, , ;……
![]() 二、如图所示,正方形网格中的每个小正方形边长都是1,每个小格顶点为格点,以格点为顶点分别按下列要求画一个三角形:(10分)
二、如图所示,正方形网格中的每个小正方形边长都是1,每个小格顶点为格点,以格点为顶点分别按下列要求画一个三角形:(10分)
(1)
使三角形的三边分别为3、![]() 、
、![]() ;(在图①中画图)
;(在图①中画图)
(2)
|
|
图① 图②
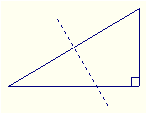
三、如图,小将同学将一个直角三角形的纸片折叠,A与B重合,折痕为DE,若已知AC=10㎝,BC=6㎝,你能求出CE的长吗?(10分)
|
|
|
|
|
|