06初三“一模”参考答案及评分建议
一、选择题
1.B 2.D 3.C 4.D 5.C
6.A 7.C 8.D 9.B 10.A
二、填空题
11. 向上 (-1,-2) [第1个空1分,第2个空2分]
12. ![]()
13. 3 8 [两个空全填对3分,只填对一个空给2分]
14. 16 -1 3 [每个空1分,第2、3空顺序可交换]
15. 70°
16 ![]()
三、解答题
17.(本小题满分9分)
解:原式=-1-2×![]() +1+2×
+1+2×![]() ……………………………… 4分
……………………………… 4分
=-1-![]() +1+2
+1+2![]() ……………………………………… 6分
……………………………………… 6分
=![]() ……………………………………………………………… 9分
……………………………………………………………… 9分
18.(本小题满分9分)
证法一:由已知条件知,⊿ABC和⊿AMN
都是等腰三角形(A为共公顶点)…………………………………………… 3分
过点A作BC所在直线的垂线m,根据“三线合一”定理可知…………… 5分
这两个等腰三角形底边上的中线和顶角的平分线均在m上,
而且这条直线是它们共公的对称轴…………………………………………… 7分
所以B、C关于m对称,M、N关于m对称,
所以BM=CN(轴对称性质)……………………………………………… 9分
证法二:∵AB=AC,AM=AN
∴∠ABC=∠ACB,∠M=∠N(等边对等角)………………………… 3分
∴∠ABM=∠ACN(等角的补角相等)…………………………………… 5分
∴∠BAM=∠CAN(三角形内角和定理)
在⊿ABM和⊿ACN中
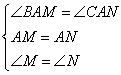 ……………………………………………………………… 7分
……………………………………………………………… 7分
∴⊿ABM≌⊿ACN(ASA)…………………………………………… 8分
∴BM=CN(全等三角形对应边相等)………………………………… 9分
说明:若学生直接用“AAS”证全等,也算正确,不扣分。
19.(本题满分9分)
解:原式=![]() …………………………………………………………… 4分
…………………………………………………………… 4分
=![]() …………………………………………………………………… 6分
…………………………………………………………………… 6分
当x=2时………………………………………………………………… 7分
原式=![]() ……………………………………………………………………… 8分
……………………………………………………………………… 8分
=-5……………………………………………………………………… 9分
20.(本题满分11分)
解:根据三角形三边关系及已知条件,可得
![]() ……………………………………………………… 5分
……………………………………………………… 5分
解(1)得:m<-2………………………………………………………… 7分
解(2)得:m>-5………………………………………………………… 9分
∴原不等式组的解集为 -5<m<-2
经检验,m的取值范围符合题意……………………………………………… 11分
[最后一句“经检验,m的取值范围符合题意”没有的话,不扣分]
21.(本题满分10分)
解:(1)2+6+14+18+10=50
从图中可知,该班共有50名学生……………………………… 4分
(2)(6+14+18+10)÷50×100%=96%
全班数学成绩及格率为96%…………………………………… 7分
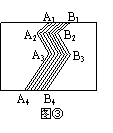 (3)从图中可知,80~90这个分数段学生最多……………… 10分
(3)从图中可知,80~90这个分数段学生最多……………… 10分
22.(本小题满分14分)
解:(1)如右图,图画正确,给…………… 3分
(2)S1= ![]() ,S2=
,S2=![]() ,S3=
,S3=![]() …………… 9分
…………… 9分
[每个空2分,共6分。解题思路:由长方形和平行四边形的面积公式,得S1=ab-b。在图②中,过A2、B2作直线,把原图形分割成上下两部分(长仍为a,宽分别为b1、b2,且b1+b2=b),则有S2=(ab1-b1)+(ab2-b2)=a(b1+b2)-(b1+b2)=ab-b,对于有两个折点的图形,同样可以分割成三部分,同理可求得S3=ab-b;]
(3)S4= ![]() …………………………………………………………… 11分
…………………………………………………………… 11分
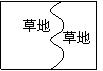 结合(2)中的三种情况,可以猜想原题图④中草地的面积应为S4=ab-b。其理由是:把左侧草地向右平移一个单位(相当于把阴影部分挖去,如图所示),则小路左右边线重合,两块草地便拼成一个宽为b,长为(a-1)的长方形,当然面积为b(a-1),即ab-b
结合(2)中的三种情况,可以猜想原题图④中草地的面积应为S4=ab-b。其理由是:把左侧草地向右平移一个单位(相当于把阴影部分挖去,如图所示),则小路左右边线重合,两块草地便拼成一个宽为b,长为(a-1)的长方形,当然面积为b(a-1),即ab-b
…………………………………………………………………………… 14分
23.(本小题满分12分)
解:设该队胜x场,平y场…………………………………………………… 1分
根据题意,可得![]() …………………………………… 7分
…………………………………… 7分
解该二元一次方程组,得![]() …………………………………………… 11分
…………………………………………… 11分
答:此队胜6场,平4场。
24.(本小题满分14分)
解:(1)∠ACE+∠BCF=45°………………………………………… 2分
(2)是………………………………………………………………………… 5分
(3)能………………………………………………………………………… 6分
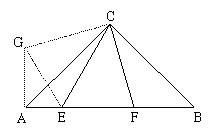
证明:把⊿CBF绕点C顺时针旋转90°得⊿CAG
使CB与CA重合,连结GE………………………………………………… 9分
根据旋转性质,∠ACG=∠BCF,AG=BF,CG=CF
∴∠ECG=∠ECA+∠ACG=∠ECA+∠BCF=45°……… 11分
在⊿ECG和⊿ECF中
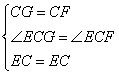
∴⊿ECG≌⊿ECF中
∴EG=EF…………………………………………………………………… 13分
∵∠GAC=∠B=45°
∴∠GAE=∠GAC+∠CAE=45°+45°=90°
∴⊿GAE是以GE为斜边的直角三角形,而GE=EF,AG=BF
 ∴AE、EF、FB能组成以EF为斜边的直角三角形…………………… 14分
∴AE、EF、FB能组成以EF为斜边的直角三角形…………………… 14分
25.(本小题满分14分)
解:(1)与⊿AEG相似的三角形分别为:
⊿ACD、⊿CFH、⊿ACB…………………………………… 3分
(2)在Rt⊿ABC中,AB=3,BC=4,
AC=![]() =5…………………………………………… 4分
=5…………………………………………… 4分
由⊿AEG∽⊿ACD得![]() ,得AE=
,得AE=![]() GE
GE
同理得CF=![]() FH………………………………………………… 6分
FH………………………………………………… 6分
AE+EF+FC=AC,
即![]() GE+EF+
GE+EF+![]() FH=5,
FH=5,
![]() (GE+FH)+EF=5
(GE+FH)+EF=5
∵EG+FH=EF,∴![]() EF+EF=5,
EF+EF=5,
EF=![]() ……………………………………………………………… 8分
……………………………………………………………… 8分
(3)若EG=x,∵⊿AEG∽⊿ACD
∴![]() ,即
,即![]() ,得AG=
,得AG=![]() x…………………… 9分
x…………………… 9分
由EG+FH=EF
得FH=EF-EG=![]() -x
-x
又由⊿CFH∽⊿CAB,
同理可得CH=![]() (
(![]() -x)…………………………………… 10分
-x)…………………………………… 10分
S=S⊿AEG+S⊿CFH
=![]() AG·EG+
AG·EG+![]() CH·FH
CH·FH
=![]() ·
·![]() x·x+
x·x+![]() ·
·![]() (
(![]() -x)·(
-x)·(![]() -x)
-x)
=![]() ………………………………………………… 12分
………………………………………………… 12分
其中自变量x的取值范围为0<x<![]() ………………………… 13分
………………………… 13分
通过配方,S=![]()
∴S的最小值为![]() ……………………………………………… 14分
……………………………………………… 14分
